尺度自适应弹载目标跟踪方法对比研究*

王曙光，石胜斌，杨传栋

(陆军炮兵防空兵学院，合肥 230031)

0 引言

随着精确制导武器在现代战争中的广泛使用，图像制导技术逐渐成为导航与制导领域的研究热点[1]，目标跟踪技术作为其关键环节，相关的研究也在不断深入。

基于图像制导的目标跟踪基本过程为：摄像头实时摄取(包括目标图像在内)景物空间图像，系统经分析处理后，逐场或逐帧计算出目标图像形心或矩心及相关匹配点坐标相对于坐标原点的偏离量，并逐场或逐帧输送给伺服系统。在运动的过程中，目标可能会呈现一些图像上的变化，比如姿态或形状的变化、尺度的变化、背景遮挡或光线亮度的变化等，给目标跟踪带来不利影响。目标跟踪算法的研究也围绕着解决这些问题而展开。

由于导弹在目标跟踪过程中，导弹与目标的距离不断发生变化，目标在视野中的尺寸大小势必会发生变化，若目标尺度扩大，由于跟踪框未能及时随之增大，跟踪器仅能得到目标的部分纹理信息；反之若目标尺度变小，则跟踪器中会引入过多的背景信息，这两种情况都会导致漂移而造成跟踪失败。与此同时弹载平台的目标跟踪需满足实时性要求，因此相关目标跟踪算法应具有较高的运算速度。

文中基于KCF算法，采用尺度池以及尺度滤波器两种方法分别对原算法进行改进，减少了对尺度变化目标的模型飘移程度，使得跟踪精度得到明显提高，同时对比了两种改进算法。

1 核化相关滤波器

KCF算法[2]全称为核化相关滤波算法，该算法利用循环矩阵在目标区域进行循环位移构造大量样本，解决了目标跟踪过程中训练样本过少的问题，同时利用循环矩阵对角化的性质使得计算大大简化。将线性空间的脊回归函数通过高斯核函数映射到非线性空间，并同样可以利用循环矩阵的性质简化计算，因此该算法具有较高的跟踪速度以及较好的跟踪精度。其基本流程如图1所示[2]。

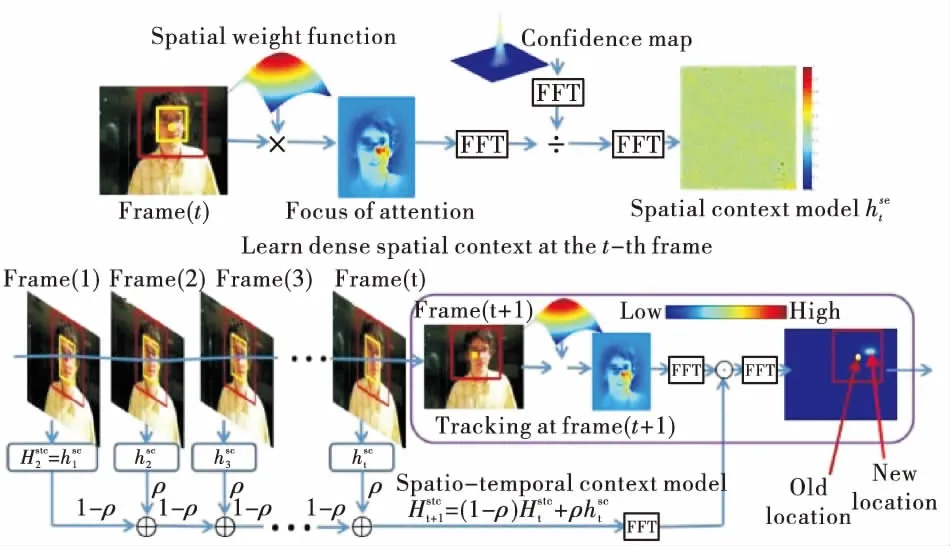
图1 KCF跟踪流程

问题可以表示为：f(z)=wTz

利用脊回归的方法，其优化函数可由最小二乘以及正则项组成：

minw∑i(f(xi)-yi)2+λ‖w‖2

(1)

若直接求解可得：

w=(XTX+λI)-1XTy

(2)

由于共轭以及求逆的计算量较大，故引入核函数将问题简化为：

α=(K+λI)-1y

(3)

利用循环矩阵有关性质，将训练过程进一步简化为：

(4)

式中：符号^表示复域的计算，由此即可用此滤波器来对输入图像进行相关性检测得到跟踪结果，用公式表示为：

(5)

文中采用模拟实验的方法，利用沙盘模拟战场环境，使用无人机系挂摄像机模拟弹载摄像头采集视频跟踪数据。在MATLAB平台上利用相关算法进行模拟跟踪实验，通过手动标注第一帧图像中的目标位置，观察记录相关滤波跟踪器在之后每一帧中的跟踪效果，实验结果如图2所示，可见在第一帧标定目标位置后，跟踪器在后续帧对目标进行跟踪，但在目标发生尺度变化时，跟踪框大小没有随之调整,有些情况下甚至发生了漂移。

图2 KCF跟踪效果

2 尺度自适应

由于KCF采用单一尺度，当目标发生尺度变换会导致精度降低，本节采取两种不同的尺度自适应策略对KCF跟踪器进行改进。

2.1 尺度滤波器

尺度滤波器[3]与位置滤波器相对独立，即通过KCF滤波器得到目标的位置信息，此时目标尺度仍为前一帧的尺度；对于目标的尺度变化，采取单独训练尺度滤波器的方法，即以当前帧的中心位置为基准，获得不同尺度的候选框，并分别提取特征，通过相关滤波计算最匹配的尺度。考虑到相邻帧目标的尺寸通常不会突变[4]，故本算法中目标样本框尺寸的选择原则为：

(6)

式中，a为尺度因子，本算法中取a=1.02；H、W分别为前一帧中目标的高和宽；S为尺度数。由式(6)可知尺度的选择不是线性的，而是越接近上一帧目标框的尺寸选择步长越小，反之越大。即是一种由细到粗的比较过程。实验结果如图3所示，可见随着目标尺度变化，跟踪模型也随之调整，能够保证在获取目标完整信息的同时引入较少的背景信息，一定程度上达到了制度自适应的效果。

2.2 尺度池

尺度池[5]的策略很简单，就是在确定目标区域时对初始目标做若干个尺度的缩放，经相关滤波器得到对应响应值，最大响应值所对应的尺度即为此时目标尺度。算法过程如图4所示。

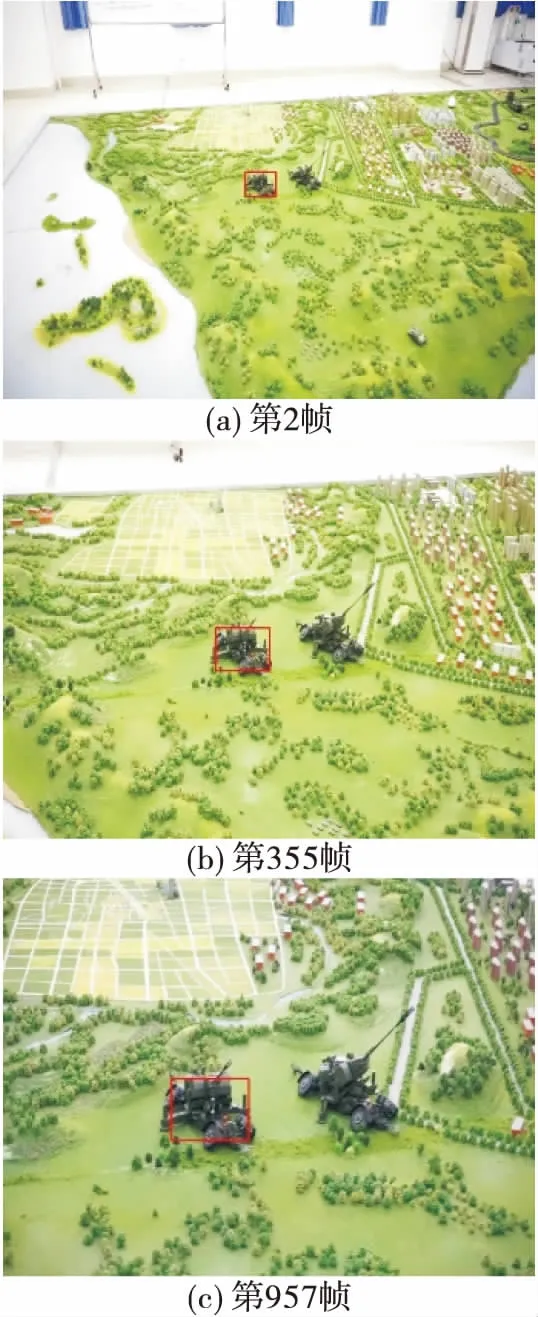
图3 KCF+尺度滤波器跟踪效果

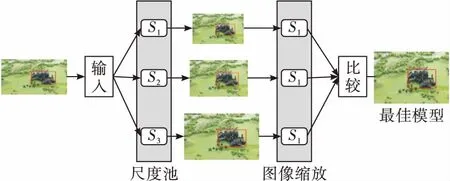
图4 尺度池方法示意图

由于导弹打击过程中，视场中目标尺度多为逐渐变大，并且要兼顾实时性要求，故本实验中所采用的尺度池为S={0.995，1.000，1.005，1.010，1.015，1.020，1.025}7个尺度，实验结果如图5所示。可见随着目标尺度变化，跟踪框大小也随之调整，因此取得了更好的效果。

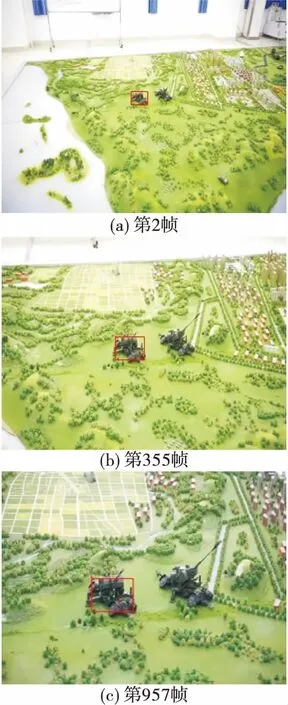
图5 KCF+尺度池跟踪效果

3 对比实验

本实验中，将KCF、KCF+尺度滤波器(简称为scale1)、KCF+尺度池(简称为scale2)3种算法进行对比实验，选取目标跟踪测试集OTB50[6]中具有尺度变化的28个图片序列进行测试，进而得到3种算法的精度图、成功率图以及运行速度。

实验结果如图6、表1所示。

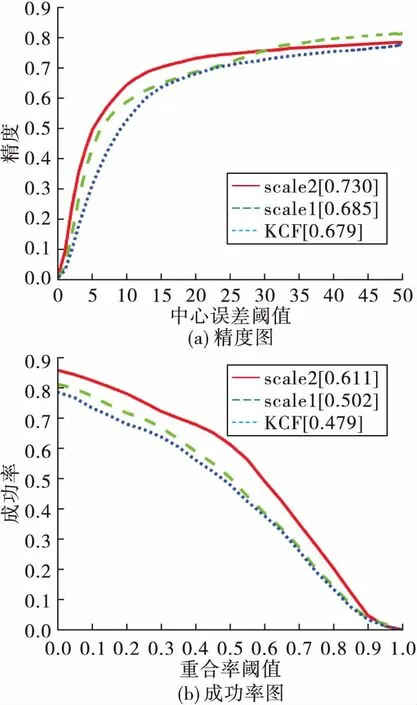
图6 OTB50尺度变化测试结果

表1 算法运行速度对比

滤波器尺度自适应方式跟踪速度/(帧/s)KCF无161scale1尺度滤波器43scale2尺度池85

通过实验发现，当中心误差阈值为20像素时，scale1、scale2方法精度较KCF分别提升了0.9%、7.5%；当重合率阈值为0.5时，成功率较KCF分别提升了27.6%、4.8%，均有比较明显的提升。加入尺度池的方法由于计算较为简单，故相比于结合尺度滤波器的方法，具有更高的运行速度。

4 小结

在应对弹载视频目标跟踪中尺度变化的问题时，采用尺度自适应方法对跟踪效果有明显提升。尺度滤波器方式精度最高但计算量较大，需对其尺度空间结构做进一步的优化；采用尺度池的方式运算速度较快，由于导弹运动规律可循，故可以结合弹目运动关系，有针对性地调整尺度池中的尺度参数，使该算法能够达到兼顾实时性与跟踪精度的目的。