局部低秩提升法MIMO雷达成像*
2020-07-09胡仁荣童宁宁何兴宇
胡仁荣,童宁宁,何兴宇,陈 桥
(空军工程大学防空反导学院,西安 710051)
0 引言
MIMO成像是近年来国内外研究的热点,成像时通过多阵元发射、多阵元接收的形式来满足空间采样的需要,将压缩感知技术应用于MIMO成像,可大幅提升雷达成像分辨率。将压缩感知理论应用于雷达成像需要解决信号的稀疏表示、测量矩阵的设计和重构算法三大关键技术。传统的算法比如基追踪算法、贪婪算法等,能对传统稀疏信号实现高效的重构。然而传统基于压缩感知的MIMO雷达成像都是将目标考虑为点目标进行成像,可能无法真实反映目标的真实结构尺寸等信息,这是由于目标连续区域的回波信号往往会表现出块稀疏结构特性[1],基于块稀疏恢复理论的MIMO雷达成像可更好的重构恢复目标像,进一步反映目标的真实信息。许多学者针对其特殊的结构,提出块稀疏算法。文献[2]提出块正交匹配追踪算法;文献[3]提出l2/l1范数最小化算法;文献[4]提出了具有模式耦合思想的PCSBL算法(pattern-coupled sparse bayesian learning);文献[5]提出了局部低秩提升(localized low-rank promoting,LOOP)算法,根据回波信号块局部结构平滑现象所表达的内在结构系数的相关性,将目标稀疏回波信号的连续系数划分为多个2×2维矩阵,通过局部低秩提升函数和对数行列式函数等工具,利用最小优化算法实现对稀疏信号的高效重构。
文中引入局部低秩提升LOOP算法,并将其应用到MIMO雷达成像中,充分挖掘目标回波信号的低秩和块稀疏结构特性,实现了对MIMO雷达目标像的高质量重构。
1 MIMO线阵回波模型
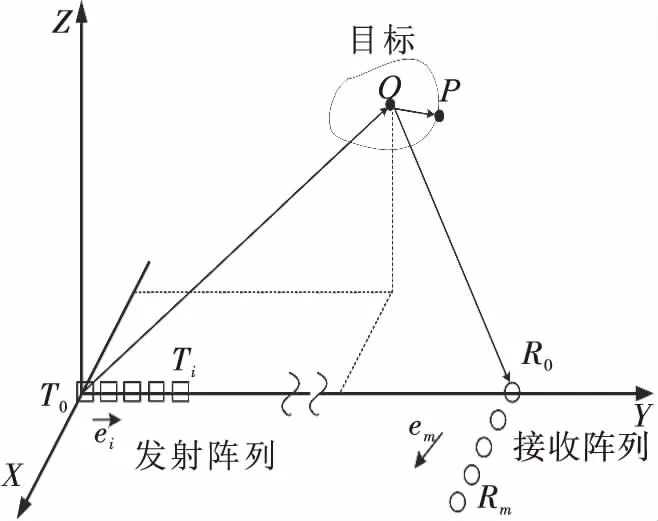
图1 MIMO雷达阵列模型示意图
建立MIMO阵列信号回波模型。如图1中均匀线阵组成是It个发射阵元和Mr个接收阵元。间距分别为dt和dr。三维坐标系的原点是第一个发射阵元,X-Y平面与阵列对应,其中发射阵为Y轴。第i个发射阵元的位置用Ti表示,第m个接收阵元位置用Rm表示,坐标原点是T0。
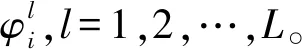
(1)
式中:T为信号子脉冲长度;fc为信号载频。不同发射信号之间相互正交,即
(2)
第m个接收阵元的回波信号,是第i个发射阵元的信号被目标散射中心P散射后经过匹配滤波分离的信号,可表示为:
(3)
式中:发射波形的自相关函数是αi(t);延时是τp,i,m=(TiP+PRm)/c;第i个发射阵元到散射中心P的距离为TiP和第m个接收阵元到散射中心P的距离为PRm。
指定目标散射中心O为参考点且O为相对坐标系的原点,P点在该相对坐标系中的坐标为(Px,Py),那么目标运动不会改变坐标(Px,Py)。因此式(3)可近似为:
(4)
式中:相位中心参考点为O,发射信号的波长为λ,回波信号经过相位补偿后可表示为:
(5)
由文献[7]和文献[8]中的引理进行推导,可得到具有D个散射中心的目标回波信号为:
(6)
式中:σp=ζp(-j2π(OP)T(T0O/T0O+OR0/OR0)/λ),(xp,yp)为包含目标散射中心P的位置信息(Px,Py)的位置参数。
2 局部低秩提升算法
2.1 MIMO成像算法评价方法
衡量各个算法的成像性能时,应采用定性和定量分析相结合的办法,既要观察成像结果是否反映目标真实信息,还要对成像结果相接近的进行定量分析,可以采用图像熵(image entropy, IE)和图像对比度两个指标进一步定量分析成像效果。两个指标定义为:
(7)
(8)
式中:目标图像用I表示,和值用Sum{·}表示,图像中元素值平均值用Ave{·}表示。IE和IC值均反映图像中目标的聚集特征,熵值IE越低,对比度IC越高,代表着成像性能越好。
2.2 局部低秩信号模型
结合MIMO雷达实际成像场景,考虑一个块稀疏信号x∈RM×1恢复问题。
y=Ax+w
(9)
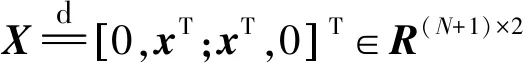

图2 矩阵X转置示意图
定义Xi(1≤i≤N)为2×2维矩阵,由矩阵X的第i行和第(i+1)行构成,则
(10)
显然,如果xi-1、xi和xi+1是非0且局部平滑的,则是一个近似秩为1的矩阵。通过观察图2这个模型可以发现,通过提高矩阵Xi的低秩性来寻求块稀疏和局部平滑的解x。更精确的说,这个问题可以描述为:
(11)
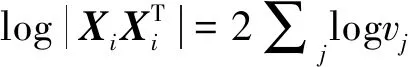
(12)
式中:E是一个正定矩阵,用来确保对数函数满足定义。因此可以将E设置为:
(13)
式中:δ为一个非常小的正数,κ(-1<κ<1)为一个参数,则式(12)可最终表示为一个没有约束条件的优化问题。
(14)
式中:λ为控制低秩和适应误差的权衡参数。
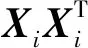
(15)
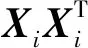
(16)
令θi表示两个矢量[xi-1,xi]T和[xi,xi+1]T的夹角,则式(16)的第二项可以表示为:
log(1-cos2θi)=2log|sinθi|
(17)
因此
(18)
式(18)中的右边的第一项表示交叉系数的对数和函数,用来促进块稀疏化的求解。式(16)中的第二项倾向于|sinθi|值较小的解,从而可能实现解的局部平滑。
2.3 迭代加权算法
利用文献[9]提出最小优化(majorization-minimization,MM)算法,通过迭代最小化目标函数的上界来求解。文献[7]和文献[8]表明对数行列式函数的代理函数为:
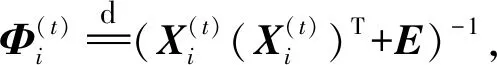
(20)
令
(21)
把式(10)和式(21)代入式(20)得:
(22)
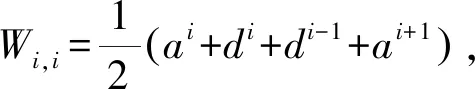
最后,使式(14)中的目标函数具体化的代理函数可表示为:
(23)
因此,优化式(14)可以通过迭代最小化式(23)来代替,式(20)的最优解为:
x=(ATA+λ-1W)-1ATy
(24)
通过迭代最小化Q(x|x(t)),能保证目标函数L(x)在每次迭代过程中不递增。
归纳上述分析过程,总结出基于LOOP算法的MIMO雷达成像流程如下:
输入:观测信号y,感知矩阵A以及参数λ和κ;
输出:雷达信号x。
1)给出一个初始雷达信号x(0),并且设置t=0;
2)当未达到收敛条件时,循环;
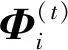
4)计算新的稀疏雷达估计信号,记为x(t+1);
6)δ(t+1)=δ(t)/10;
7)停止迭代,否则
8)t=t+1;
9)结束循环。
3 仿真与结果分析
MIMO阵列排布如图1所示。仿真目标的点散射模型如图3所示,目标质心O(0,0,20 000),单位m。设发射天线It=4个,阵元间距为dt=12 m,接收天线Mr=25个,接收天线间距为dr=12 m。雷达发射信号的载波频率为10 GHz,雷达采样频率为5 GHz,发射信号采用4个正交性和接收正交分离性均较好的正负LFM信号,以发射阵列第一个阵元T0作为测量坐标系的坐标原点,以参考相位中心点O为相对坐标系原点。
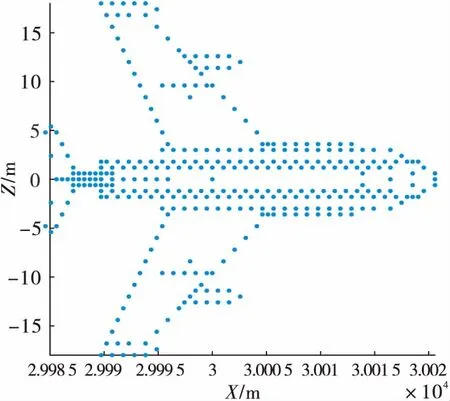
图3 散射点模型
图4是包括LOOP算法在内的各种算法对目标模型的成像效果。
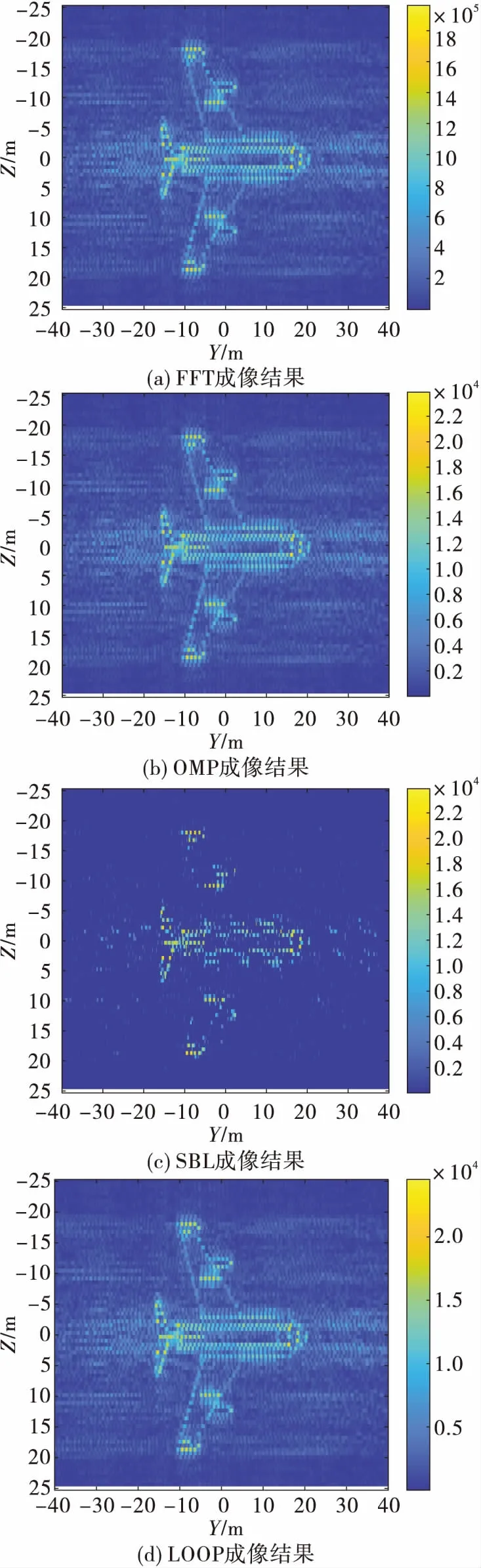
图4 各算法成像效果图
分别计算图4中各算法成像图的IE和IC值,可得
IEFFT=5.291 5,IEOMP=5.423 5,IESBL=3.713 7,IELOOP=5.193 9;
ICFFT=7.664 7,ICOMP=7.653 2,ICSBL=7.433 7,ICLOOP=7.703 2。
通过对比分析可以发现,基于LOOP算法的MIMO雷达成像方法较传统的压缩感知算法能更好的实现目标像的重构。
4 结论
传统的压缩感知算法往往无法实现块稀疏信号重构,应用到MIMO成像时会影响精度,从而无法较精确的反应目标的真实信息,文中通过局部低秩提升算法挖掘MIMO雷达回波信号的块稀疏特性,进而实现MIMO雷达目标像的高质量重构。
