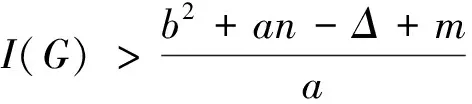An Isolated Toughness Condition for All Fractional(g,f,n,m)-Critical Deleted Graphs
2020-07-08LanMeihuiGaoWei
Lan Meihui Gao Wei
(1.School of Information Engineering, Qujing Normal University, Qujing 655011, China;2.School of Information Science and Technology, Yunnan Normal University, Kunming 650500, China)
Abstract As a parameter to measure the vulnerability of networks, the isolated toughness of a non-complete graph G is defined by where i(G-S)is denoted by the number of isolated vertices in G-S. Otherwise, I(G)=∞ for a complete graph G. In this paper, we study the relationship between the isolated toughness and all the fractional(g,f,n,m)-critical deleted graphs, and determine that G is an all fractional(g,f,n,m)-critical deleted graph if where a,b are positive integers, 1≤a≤b, b≥2 and Δ=b-a. The theoretical result obtained in our paper has potential guiding significance for network designing.Finally, we finish our paper with an open question.
Key words Data transmission network Isolated toughness All fractional factor All fractional(g,f,n,m)-critical deleted graph
1 Introduction
All graphs considered in this paper are simple and finite.LetGbe a graph with vertex setV(G)and edge setE(G).We denotedG(v)andNG(v)(simply byd(v)andN(v))as the degree and the neighborhood of any vertexvinG, respectively.ForS⊆V(G), we denote byG[S]the subgraph ofGinduced byS, and setG-S=G[V(G)S].For two vertex-disjoint subsetsS,T⊂V(G), seteG(S,T)=|{e=uv|u∈S,v∈T}|.We denote the minimum degree ofGbyδ(G)=minv∈V(G){d(v)}.The notations and terminologies used but undefined in this paper can be found in Bondy and Mutry[1].

A graphGis called a fractional(g,f,m)-deleted graph if for each edge subsetH⊆E(G)with |H|=m, there exists a fractional(g,f)-factorhsuch thath(e)=0 for alle∈H.That is to say, after removing anymedges, the resulting graph admits a fractional(g,f)-factor.A graphGis called a fractional(g,f,n)-critical graph if after delated anynvertices fromG, the resulting graph admits a fractional(g,f)-factor.A concept of fractional(g,f,n,m)-critical deleted graph can be regarded as the combination of fractional(g,f,m)-deleted graph and fractional(g,f,n)-critical graph, i.e., a graphGis to be fractional(g,f,n,m)-critical deleted if after deletingnvertices fromG, the resting graph is a fractional(g,f,m)-deleted graph.
We sayGhas all fractional(g,f)-factors ifGhas a fractionalp-factor for eachp:V(G)→Nwithg(v)≤p(v)≤f(v)for anyv∈V(G).Ifg(v)=a,f(v)=bfor each vertexvandGhas all fractional(g,f)-factors, then we say thatGhas all fractional[a,b]-factors.Lu[11]determined the sufficient and necessary condition for a graph with all fractional(g,f)-factors.Zhou and Sun[17]introduced all fractional(a,b,n)-critical graph, i.e., a graphGis an all fractional(a,b,n)-critical graph if after deleting anynvertices ofGthe remaining graph ofGadmits all fractional[a,b]-factors.Similar to fractional(g,f,m)-deleted graph and fractional(g,f,n)-critical graph, the concepts of all fractional(g,f,m)-deleted graph and all fractional(g,f,n)-critical graph can be defined.
A graphGis an all fractional(g,f,n,m)-critical deleted graph if after deleting anynvertices ofGthe remaining graph is an all fractional(g,f,m)-deleted graph.Ifg(v)=a,f(v)=bfor eachv∈V(G), then all fractional(g,f,n,m)-critical deleted graph becomes all fractional(a,b,n,m)-critical deleted graph, i.e., after deleting anynvertices ofGthe remaining graph is still an all fractional(a,b,m)-deleted graph.Gao et al.[8]presented the sufficient and necessary condition for a graph to be all fractional(g,f,n,m)-critical deleted.In computer science, a graph corresponding to data transmission network has all fractional(g,f)-factor which reveals that the data packets within a certain capacity range can be transmitted at a moment.The concept of all fractional(g,f,n,m)-critical deleted graph implies that the data packets within a certain capacity range can be still transmitted when certain sites and channels are blocked or damaged.
Inspired by the idea of toughness, Yang et al.[12]introduced the notion of isolated toughness to measure the vulnerability of the network, which was stated as follows: ifGis a complete graph,I(G)=∞; otherwise,
wherei(G-S)is the number of isolated vertices ofG-S.
There are several works contributing to the relationship between isolated toughness and fractional factors.Li et al.[9]determined thatGis a fractionalk-deleted graph fork≥2 ifδ(G)≥k+1 andI(G)>k, and they also show that the isolated toughness bound is sharp fork-deleted graph.Zhou and Pan[16]studied an isolated toughness condition for a graph to be fractional(a,b,k)-critical.Zhou et al.[15]presented an isolated toughness condition for fractional(g,f)-factors.Gao and Wang[7]computed a new isolated toughness condition for fractional(g,f,n)-critical graphs.Gao et al.[5]derived an isolated toughness condition for graphs to be fractional(k,m)-deleted graphs.More results on the topic with fractional factor, fractional deleted graphs and other applications can refer to Gao and Gao[3], Zhou et al.[13,14,18,19], Gao et al.[2,4,6].
In this paper, we study the relations between isolated toughnessI(G)and all fractional(g,f,n,m)-critical deleted graph.Our main result can be formulated as follows.
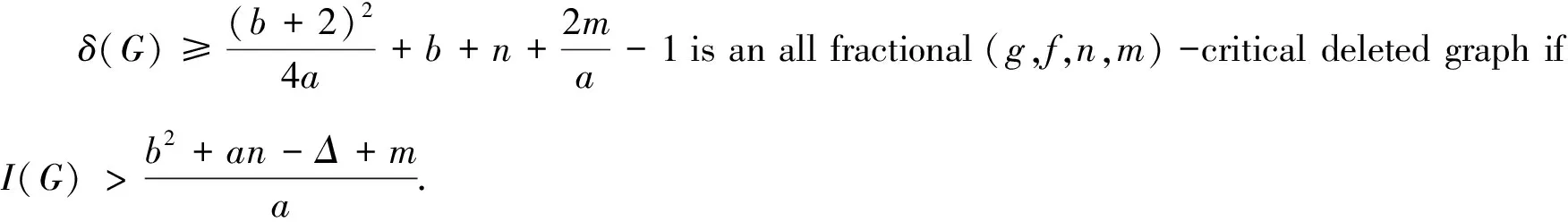
The isolated toughness result presented in Theorem 1 expands the original conclusion manifested in Gao et al.[5]and Gao and Wang[7], respectively.
To prove Theorem 1, we depend heavily on the following lemma which characterises the necessary and sufficient condition of all fractional(g,f,n,m)-critical deleted graphs.
Lemma 1(Gao et al.[8]) Letmandnbe nonnegative integers.Letg,f:V(G)→Z+be two valued functions withg(x)≤f(x)for eachx∈V(G), andHbe a subgraph ofGwithmedges.ThenGis all fractional(g,f,n,m)-critical deleted if and only if
for any non-disjoint subsetsS,T⊆V(G)with |S|≥n.
The following two lemmas are presented by Liu and Zhang[10]which will be used in our proof.
Lemma 2(Liu and Zhang[10]) LetGbe a graph and letH=G[T]such thatδ(H)≥1 and 1≤dG(x)≤k-1 for everyx∈V(H)whereT⊆V(G)andk≥2.LetT1,…,Tk-1be a partition of the vertices ofHsatisfyingdG(x)=jfor eachx∈Tjwhere we allow someTjto be empty.If each component ofHhas a vertex of degree at mostk-2 inG, thenHhas a maximal independent setIand a covering setC=V(H)-Isuch that
wherecj=|C∩Tj| andij=|I∩Tj| forj=1,…,k-1.
Obviously, Lemma 2 is also hold forδ(H)≥0.In light of the proving process of Lemma 2.2 in[10], we derive the following Lemma.
Lemma 3(Liu and Zhang[10]) LetGbe a graph and letH=G[T]such thatdG(x)=k-1 for everyx∈V(H)and no component ofHis isomorphic toKkwhereT⊆V(G)andk≥2.Then there exists an independent setIand the covering setC=V(H)-IofHsatisfying
and

2 Proof of main result

(1)
We selectSandTsuch that |T| is minimum.Thus, we immediately getT≠φ, anddG-S(x)≤b-1 for anyx∈T.
Letlbe the number of the components ofH′=G[T]which are isomorphic toKband letT0={v∈V(H′)|dG-S(v)=0}.LetHbe the subgraph inferred fromH′-T0by deleting thoselcomponents isomorphic toKb.LetS′ be a set of vertices that contains exactlyb-1 vertices in each component ofKbinH′.
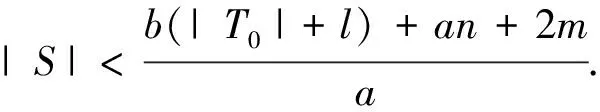
and

LetH=H1∪H2whereH1is the union of components ofHwhich satisfies thatdG-S(v)=b-1 for each vertexv∈V(H1)andH2=H-H1.By means of Lemma 3,H1has a maximum independent setI1and the covering setC1=V(H1)-I1such that
(2)
and
(3)

(4)
wherecj=|C2∩Tj| andij=|I2∩Tj| for everyj=1,…,b-1.SetW=V(G)-S-TandU=S∪S′∪C1∪(NG(I1)∩W))∪C2∪(NG(I2)∩W).We yield
|C2|+|NG(I2)∩W|=|V(H2)|-|I2|+|NG-S-T(I2)|
=|V(H2)|-|I2|+|NG-S(I2)|-|NT(I2)|
=(|V(H2)|-|I2|-|NT(I2)|)+|NG-S(I2)|
≤(|V(H2)|-|I2|-|NH2(I2)|)+|NG-S(I2)|
Furthermore, we get
(5)
and
(6)
wheret0=|T0|.Wheni(G-U)>1, we have
|U|≥I(G)i(G-U).
(7)
Ifi(G-U)=1, thenG[T]is a clique and |V(G[T])| and for anyx∈T.This leads a contradiction, and it reveals(7)always established. Followed from(5)-(7), we yield (8) In light ofb|T|-dG-S(T)≥a|S|-an-2m+1, we have Combining with(8), we derive (9) In view of(2)and(3), we get (10) By means of(4),(9)and(10), we have (11) In what follows, we discuss the following cases according to the value oft0+l. Case 1t0+l≥1.In this case, by(11)and(aI(G)-b)(t0+l)-an-2m+1-la(b-1)>(b2+an-Δ+m-b)(t0+l)-an-2m+1-la(b-1)≥-m+1, we have (12) Claim 1Ift0+l≥1, then |I2|≠0. ProofSuppose |I2|=0.Then |I1|≠0 by |V(H)|>0 and(12)becomes (13) a contradiction.The last step follows from |I1|≥1. Claim 2Ift0+l≥1, then |I1|≠0. ProofSuppose |I1|=0.We yield |I2|≠0 by |V(H)|>0 and(12)becomes Note that (b-2)(b-j)-aI(G)+aj+b-j <(b-2)(b-j)-(b2+an-Δ+m)+aj+b-j =-a+j(a-b+1)-m-an≤-m-1. We get a contradiction. From Claim 1 and Claim 2, we can see that |I1|>0 and |I2|>0.According to |I2|≥1 and we infer or (14) a contradiction. Case 2t0+l=0.In this case, by(11)we deduce -an-2m+1. (15) Claim 3Ift0+l=0, then |I2|≠0. Using(15), we derive +an+2m-1≥0. (16) a contradiction. Claim 4Ift0+l=0, then |I1|≠0. ProofSuppose |I1|=0.Then |I2|≠0 using |V(H)|>0.In terms of(15), we infer This implies that |I1|≠0. which reveals (17) a contradiction. Therefore, we complete the proof of the desired result. In light of the same tricks presented here, we derive the following results on fractional(g,f,n,m)-critical deleted graph and fractional(a,b,n,m)-critical deleted graph, and the detailed proofing processes are skipped here. Through the analysis of the entire proof process, we can see that if we add additional requirement(a,b)≠(1,2), then “>” can be replaced by “≥” in the isolated toughness condition.For instance, in Claim 2 we have-a+j(a-b+1)-m-an≤-m-2, and in Claim 4 we get(a-b+1)j-a-m-an<-m-an-1 if(a,b)≠(1,2).In this way, the main results can be expressed in the following fashion.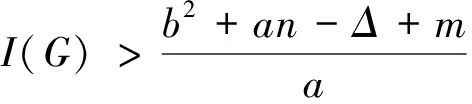
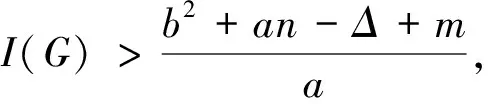
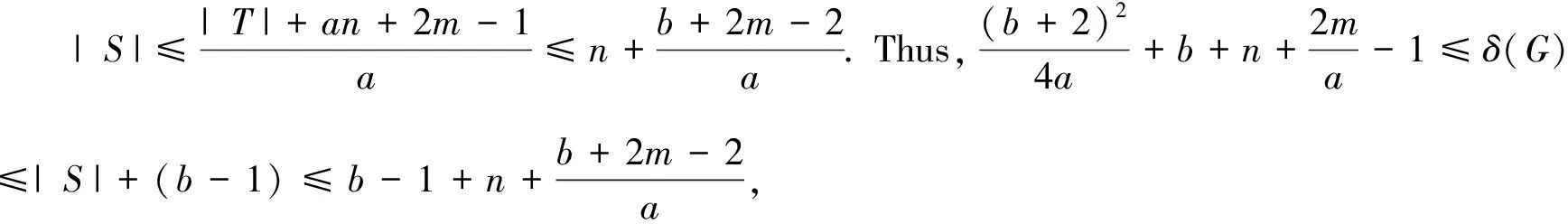
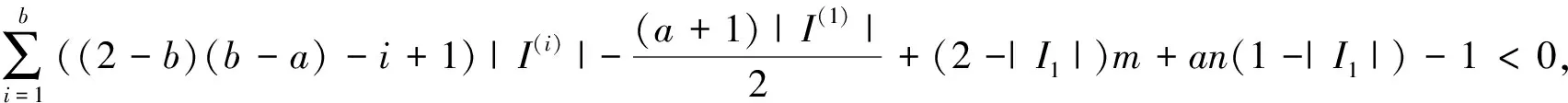
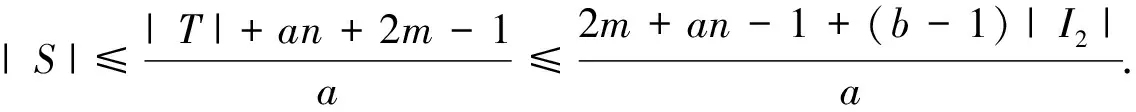
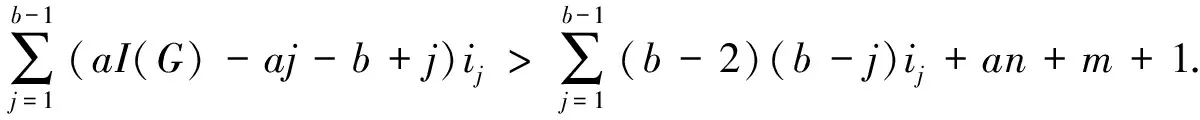
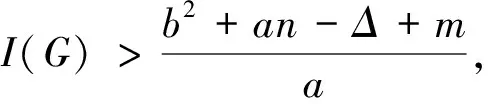
3 More related results


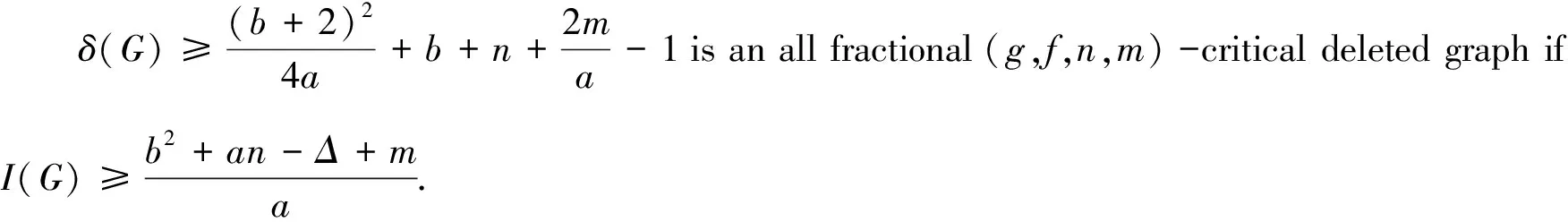


4 Conclusion and discussion