大型PCTC船车辆跳板端部铰链动载荷分析
2020-07-08黄辰,余龙
黄 辰,余 龙
(1. 上海德瑞斯华海船用设备有限公司,上海 200093;2. 上海交通大学 海洋工程国家重点实验室,上海 200240)
0 引 言
作为大型滚装船的重要组成部分,滚装通道设备对于实现滚装船的运输和装卸功能而言具有重要的作用。在通道设备中,车辆跳板是连接船舶与码头的桥梁,是车辆进出船舶的主要通道。在装卸车辆时,车辆跳板主要依靠与船体铰接的多组铰链来传递其受到的各种作用力,包括跳板自重、车辆载荷和船舶与码头相对运动产生的摩擦力。因此,对端部铰链进行强度校核是车辆跳板设计中十分重要的环节,直接关系到车辆跳板的安全性。在对铰链进行强度校核时,计算铰链受到的作用力是十分关键的,该作用力与车辆载荷有直接的关系。在对铰链进行强度规范校核时,处理车辆载荷采取的方法通常是用车辆轴载荷乘以1.1倍动载荷系数,将其转化为静载荷之后采用估算法或有限元软件进行计算,最终得到铰链的应力[1]。针对车辆跳板结构强度的相关理论和试验研究大多是基于该思想开展的[2-4]。
车辆行驶时产生的载荷往往与车速和路面平整度有很大关系[5]。一般情况下,滚装通道设备设计厂家会对车辆(尤其是大型车辆)通过跳板的速度有一定的要求。然而,在实际运营过程中,为提高装卸效率,车辆通过跳板的速度往往难以满足滚装通道设备设计厂家的要求。另外,大型滚装船车辆跳板均为多节设计,跳板节与节之间的过渡区域和跳板表面的防滑设计都可能造成车辆载荷的实际值比船级社规范规定的数值大,导致结构趋于危险。
本文提出大型滚装船跳板的动载荷计算方法,并以某巴拿马级PCTC(Pure Car and Truck Carrier)车辆艉跳板为分析对象,对其承载车辆运行的动态过程进行动力学仿真,计算得到铰链受力的动态载荷谱。相比于将车辆载荷转化为静载荷的处理方法,动力学仿真计算便于对铰链在不同车型、不同车速条件下的受力情况进行分析,并能更真实地反映出车辆载荷的实际作用情况。
1 理论基础
多体系统的动力学分析是根据牛顿定理给出自由物体的变分运动方程,并运用拉格朗日乘子定理推导出基于约束的多体系统动力学方程。MSC·ADAMS是由美国MDI公司开发的虚拟样机分析软件,依据上述方法,ADAMS可自动建立系统的动力学微分-代数方程[6],即

式(1)中:q为系统广义坐标列阵;u为系统广义速度列阵;P为系统动量;T为系统动能;φ为系统约束方程;λ为拉氏乘子列阵;F为系统广义力列阵;t为时间。为求解上述方程,ADAMS可根据机械系统特性,选择不同的数值积分算法。对于刚性系统,ADAMS采用变系数的向后微分公式(Backwards Differentiation Formulation, BDF)刚性积分程序求解,这是自动变阶、变步长的预估矫正法,分别以Index3、SI2和SI1积分格式,在积分的每一步采用修正的 Newton-Raphson迭代算法迅速、准确地求解,从而得到用户所需的各种动力学计算结果。
2 动载荷计算流程
本文采用MSC·ADAMS建立仿真模型,主要包括跳板-车辆实体模型、约束边界条件的添加和接触力的定义等3部分。完成上述3部分工作之后,即可使用ADAMS中的仿真模块对车辆通过跳板的过程进行动力学仿真,并得到铰链受力的时历谱。另外,采用有限元分析软件MSC·PATRAN/NASTRAN 建 立 跳板的FEM(Finite Element Method)模型,并根据规范要求得到静力条件下铰链的受力。最后,根据上述计算结果,对采用动力学方法和静力学方法得到的计算结果进行对比分析。铰链动载荷计算流程见图1。

图1 铰链动载荷计算流程
3 算例分析
3.1 静力分析
计算所用PCTC的跳板总长40m,车道宽5.9m,共由3节组成,总重约180t。跳板与船体中心线的夹角为 34°,完全开启用时约15min。轿车、卡车、客车和拖车等不同种类的车辆均可在该跳板上通行,其中重载车辆的载荷达150t。采用有限元分析软件MSC·PATRAN/NASTRAN对该跳板进行建模计算,得到端部铰链在满足规范要求的车辆载荷作用下的受力值。
3.1.1 有限元建模
由于车辆跳板大部分为板和梁组成的框架结构,因此采用自动化分网格的方法生成四边形单元(Quad4),整个模型共有9183个单元。为方便讨论,按从左舷到右舷的顺序将主铰链命名为主铰链A和主铰链B,将副铰链命名为副铰链1~副铰链4。车辆跳板结构见图2,车辆跳板有限元模型见图3。车辆跳板所用钢板为船用高强度钢,材料的物理属性定义为:弹性模量E=2.06×1011GPa;泊松比0.3;剪切模量G=0.792×1011GPa;屈服强度355MPa。对于跳板顶板、纵桁腹板、横梁腹板、面板和铰链眼板等直接由钢板构成的结构,其单元类型定义为2D板壳单元(shell);对于顶板上2个纵桁间的扶强材,其单元类型定义为1D梁单元(beam),梁单元截面特性根据实际设计定义。

图2 车辆跳板结构

图3 车辆跳板有限元模型
3.1.2 边界约束条件
车辆跳板打开之后,一端依靠铰链与船体铰接,另一端搭接在码头上,2节跳板之间依靠中间铰链与调节油缸连接并保持2节之间变形一致。因此,跳板模型的边界条件主要包括端部铰链与船体之间的约束、2节跳板之间铰链的约束和第二节跳板与码头之间的约束等3方面。
在设计时,车辆跳板最外侧2个主铰链沿x方向(船长方向)和z方向(垂直方向)的平移被约束为0;副铰链眼板与铰链轴之间留有2mm的间隙,因此沿x方向(船长方向)的平移被约束为0,沿z方向(垂直方向)的平移可移动2mm;第二节跳板搭接在码头上时,仅z方向的平移被约束为0。在中间铰链处,2节跳板在x方向和z方向上的变形是完全相同的;在调节油缸处,2节跳板在x方向上的相对变形是完全相同的。因此,在中间铰链和调节油缸处,需添加多点约束(Multi-Point Constrain, MPC),以保证第一节跳板和第二节跳板在这些节点变形的一致性。
车辆跳板PATRAN模型的边界约束条件见表1。

表1 车辆跳板PATRAN模型的边界约束条件
3.1.3 计算载荷和工况
车辆跳板受到自身重力和车辆载荷的作用,其中重力可由PATRAN模型自动添加计算。通过跳板的重型自卸车轴的载荷为30t,车辆总重达150t,其载荷通过5根车轴(共10组车轮)作用在跳板上。在计算时,根据车辆轴距和轮距共添加10个z方向的作用力,按规范考虑1.1倍动载荷系数,则每个作用力的大小为165000N。为全面考察各组铰链的受力情况,分别计算以下2种工况:
a) 工况一,车辆沿跳板中间区域通过并作用在跳板铰链一端;
b) 工况二,车辆沿主铰链A一侧通过并作用在跳板铰链一端。
计算得到的2种工况下各组铰链的受力见图4和图5,端部各组铰链受力值见表2。
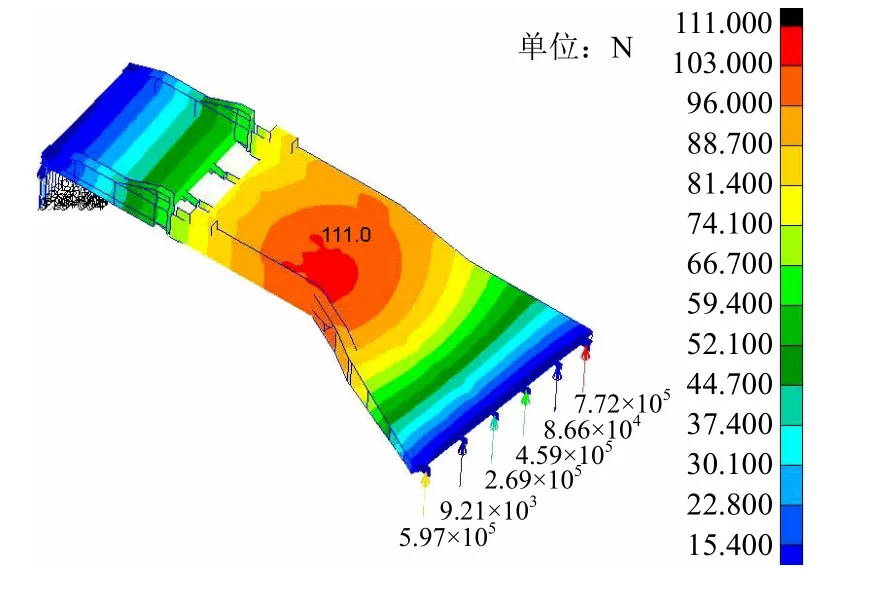
图4 工况一下各组铰链受力

图5 工况二下各组铰链受力

表2 端部各组铰链受力值 单位:kN
通过有限元计算可知,在考虑1.1倍动载荷系数的情况下,各组铰链中主铰链A的受力最大,在工况二中其受力最大值达1240kN。因此,在后续动力学仿真计算中,将重点分析车辆沿主铰链A一侧通过时主铰链A的受力情况。
3.2 动力学仿真计算
3.2.1 建立实体模型
车辆跳板的工作角度为-5.0°~8.5°,本文所述模型中跳板与水平面的夹角设为8.5°。为模拟车辆从码头经过车辆跳板驶入船体的过程,应在ADMAS实体模型中设置码头、船体和车辆跳板。由于码头和船体仅提供车辆通行路径,对端部铰链受力没有影响,因此在ADAMS中将模型简化为长方体。对于车辆跳板,模型主要考虑对跳板质量和重心位置有较大影响的主体结构和起约束作用的各处铰链,对局部加强结构不予考虑。对于通过跳板的车辆,由于本文只讨论车辆质量的影响,因此只需模拟出车辆与跳板接触的轮胎和对轮胎施加载荷的车轴。建立完成的ADAMS车辆跳板动力学仿真模型见图6。
3.2.2 添加约束条件
在通过车辆跳板装卸车辆过程中,受海浪、潮汐等外部因素的影响,车辆跳板与码头、船体之间可能存在相对移动
或转动,但这种相对运动是比较缓慢的。为合理地简化模型,可假设车辆跳板与船体、码头之间是相对静止的。对于端部铰链和2节跳板之间的中间铰链,模型采用ADAMS约束命令中的旋转副进行约束。ADAMS模型约束信息见表3。
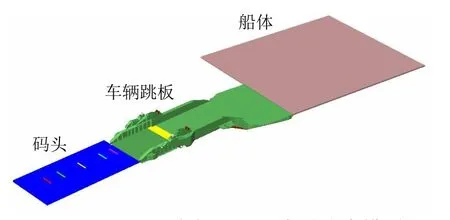
图6 ADAMS车辆跳板动力学仿真模型

表3 ADAMS模型约束信息
3.2.3 添加接触力
车轮与跳板之间和各组铰链与铰链轴之间采用ADAMS中的接触模型定义。ADAMS中的接触力主要考虑冲击力和摩擦力,分别采用冲击函数模型和库伦摩擦力模型计算。关于接触力的定义,需设置以下参数:
1) Force Exponent,即力的非线性指数,用来计算瞬时法向力中材料刚度项的贡献值,表征材料的非线性特性。对于金属,该指数常取1.3~1.5;对于橡胶,该指数可取2,甚至是3。另外,根据ADAMS帮助文件,在仿真计算中,该指数取值大于2.1通常会使碰撞模型的求解更加稳定合理。综上,本文中该指数取系统默认值2.2。
2) Damping,即阻尼系数,用来表征接触过程中的能量损失。该系数通常取刚度值的0.1%~1.0%,一般取10~100N·s/mm,本文中取系统默认值10 N·s/mm[7]。
3) Penetration Depth,即定义全阻尼(full damping)时的最大穿透深度。理论上该数值越小越逼近真实,但该值过小会影响ADAMS数值的收敛性,一般可取ADAMS推荐的0.1mm[8]。
与摩擦力有关的设置包括静摩擦因数、动摩擦因数、静摩擦转换速度和动摩擦转换速度。由于摩擦力的方向平行于车辆跳板顶板,对本文研究的垂向力的大小影响不大,因此与摩擦力有关的设置均取系统默认值,即静摩擦因数0.3,动摩擦因数0.1,静摩擦转换速度100mm/s,动摩擦转换速度1000mm/s。
3.3 动力学仿真结果分析
3.3.1 不同车型影响
分别计算150t重型车和90t中型车以10km/h的速度通过跳板时主铰链A的受力情况,结果见图7和图8。

图7 10km/h车速下150t车辆主铰链A受力

图8 10km/h车速下90t车辆主铰链A受力
根据动力学仿真计算,车辆载荷的实际作用有以下2个特点:
1) 车辆载荷会对铰链产生大于1.1倍动载荷的作用;
2) 车辆载荷不是静载荷,而是动态循环载荷。
对于跳板长度很长的大型PCTC而言,在采用静力学方法进行强度校核时,由于跳板与码头之间的摩擦力在铰链处产生的作用力一般大于车辆载荷对铰链的作用力,因此对于铰链的设计而言,危险载荷往往是摩擦力,而不是车辆载荷。另外,船级社规范中滚装设备部件的许用应力远小于材料的屈服强度,因此对于车辆载荷而言,铰链的安全裕度是很大的。
但是,根据图 7所示的计算结果,铰链的最大受力约为6.86×103kN,已远远超过摩擦力在铰链处产生的作用力。剖面形状见图9,则其平均应力τ= 239 MPa 。若考虑使用过程中的磨损、锈蚀等情况,重型车通过跳板时产生的动载荷是比较危险的,仅按传统计算方法无法真实体现出铰链受力的最不利情况。综上所述,在设计铰链时应留有足够的安全余量,以避免车辆通过跳板过渡区域时产生的瞬时动载荷对结构造成不利影响。另外,对于装载量巨大的大型汽车滚装船而言,由于车辆载荷实际上是循环载荷,因此铰链可能会发生疲劳破坏。由此可见,仅对铰链的静强度进行校核未必能全面衡量其安全性,采用动力学方法对铰链的强度进行分析十分必要。

图9 主铰链A外形图
3.3.2 不同车速影响
分别计算150t重型车以15km/h和20km/h的速度通过跳板时主铰链A的受力情况,结果见图10和图11。
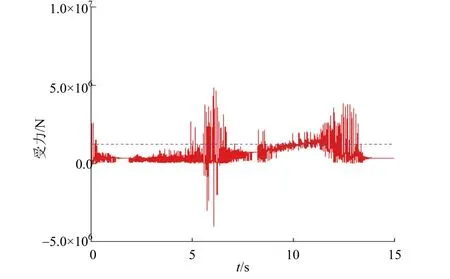
图10 15km/h车速下150t车辆主铰链A受力
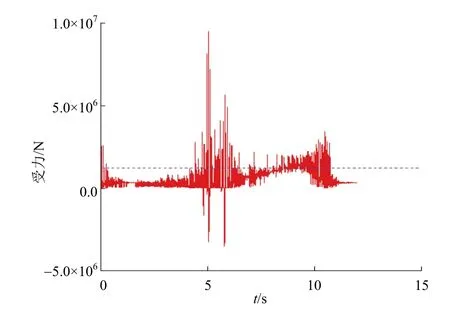
图11 20km/h车速下150t车辆主铰链A受力
由计算结果可知,车辆以15km/h和20km/h的速度通过跳板时,主铰链A受力的平均值比以10km/h的速度通过跳板时更大,因此动载荷系数也大于1.1。由于重型车辆总重很大,为防止其产生的动载荷对结构产生不利影响,在滚装船装卸车辆过程中,应严格控制重型车的车速,以免发生意外。
3.3.3 多种车型组合
分别计算3辆重型车和重型车+中型车+小型车这2种工况下3辆车连续以15km/h的速度通过跳板时主铰链A的受力情况,结果见图12和图13。在控制车辆通过跳板时,前后2辆车会在一段时间内同时行驶在跳板上,因此其载荷会产生一定的相互影响。由仿真结果可知,3辆车先后经过跳板形成的载荷谱并不是每种单一车型通过跳板时形成的载荷谱的叠加。这种相互影响也是采用静力学方法难以模拟分析的。

图12 15km/h车速下车辆主铰链A受力(重型车+重型车+重型车)
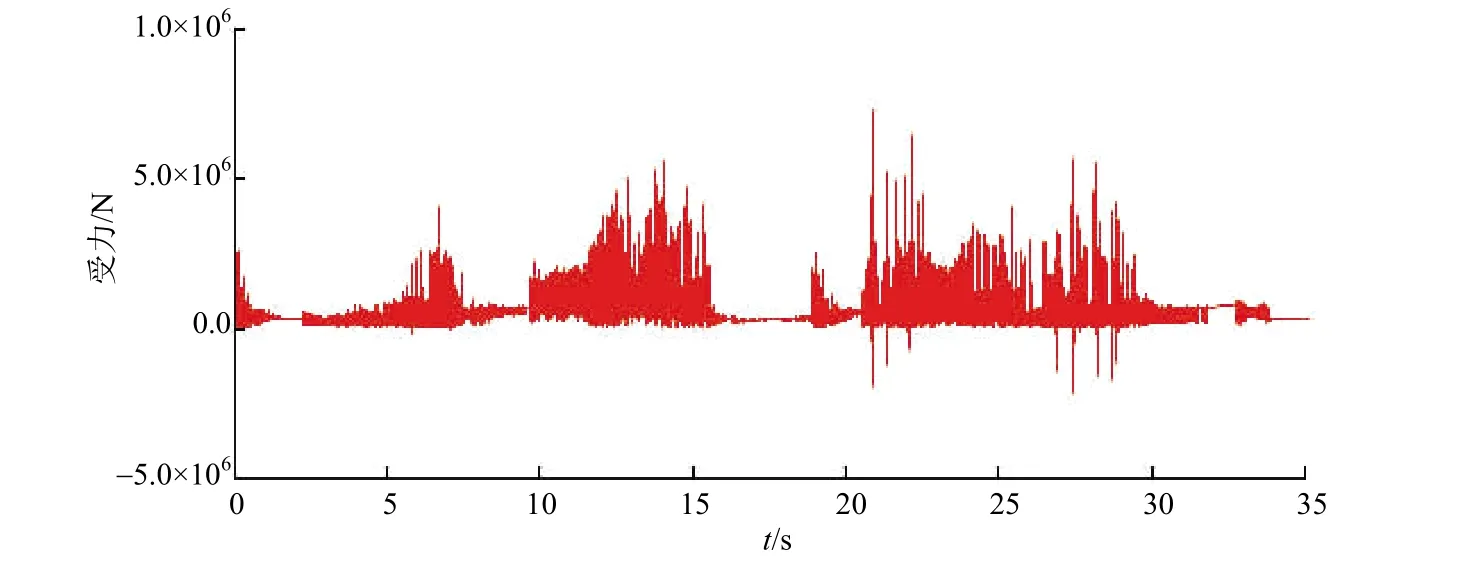
图13 15km/h车速下主铰链A受力(重型车+中型车+小型车)
由第 3.3.1节的分析和本节的计算结果可知,车辆载荷对跳板铰链的影响是十分复杂的。大型 PCTC单个航次内可能有数以千计的车辆通过车辆跳板完成装卸,车辆跳板承受循环载荷的次数可能会达到数十万次,其全寿命周期内的载荷循环次数可达107~108量级。根据疲劳强度理论,铰链并不一定在跳板全部
通过重型车的情况下破坏,仅以最大载荷来分析铰链的强度是不全面的。因此,随着汽车滚装船装载量和装载车辆总重的不断增加,应按上述方式建立不同车型组合通过跳板时铰链受力的载荷谱,以便进一步分析铰链在高应力循环次数和高平均应力条件下的疲劳强度。
综合上述计算,采用动力学方法计算车辆载荷作用下铰链的受力,可得到很多采用静力学方法计算无法得到的结果,二者之间的主要差异见表4。

表4 动力学方法与静力学方法计算结果对比
4 结 语
本文研究了汽车滚装船跳板设计分析中铰链的静载荷和动载荷,分析了车辆对跳板产生的动载荷。首先,采用有限元分析软件MSC·PATRAN计算得到了某巴拿马级PCTC车辆跳板在车辆载荷作用下铰链受力的最大值。随后,针对受力最大的主铰链A,采用多体动力学仿真软件MSC·ADAMS建立了动力学仿真模型,得到了不同车型和车辆以不同车速通过跳板时主铰链的动载荷,并与PATRAN的计算结果进行了对比。
通过静力和动力对比分析可知:采用静力分析结果的1.1倍来考虑动载荷不合适,需考虑车辆的动态作用;动力学方法既可用来校核铰链的静力学强度,又可根据计算得到的载荷谱为铰链的疲劳强度分析提供计算依据,相比传统的静力学方法,可使铰链的强度分析更全面。
