数学概念课教学的实践与思考

林美珍

摘 要初中数学概念课型是指需要单独设课讲授的、重要的定义性概念课。主要教学任务是使学生掌握所反映的一类事物的共同本质属性，以及运用概念去办事，去解决问题。教学的一般程序是：习得阶段——转化阶段——迁移与应用阶段。章建跃博士说，概念教学的核心就是概念，将凝结在数学概念中的数学家的思维打开，以典型丰富的实例为载体，引导学生展开观察、分析各事例的属性、抽象概括共同本质属性，归纳得出数学概念。如何更有效地习得概念，更灵活地迁移运用概念，需要老师由“教材”，由“学情”，仔细推敲，精心创设情境，巧妙引导，让概念课型的教学更有灵性。

关键词概念课;教材;思想;知其源;善于学;灵活用

中图分类号：G632 文献标识码：A 文章编号：1002-7661（2020）15-0202-02

概念是思维的基本形式，具有确定研究对象和任务的作用。概念的理解和掌握关系到学生基础知识的习得、基础能力的培养。概念课教学是中学数学教学的一个重要部分。概念课看似简单，实质其内容之丰富，蕴含数学味道，使学生深刻理解并非易事。笔者有幸参加厦门市直属学校片区公开课“不等式的解及其解集”的同课异构的教学研讨，“知其源，善于学，灵活用”是这堂课教学的最大体会和思考。

“知其源”，任何一个数学概念不是无中生有，强加的，都有其来源，很多蕴含着数学文化。教材分析就是“知其源”的首要体现。在教学中，通过多查阅书籍，充分备课，可以在教学中渗透数学文化，数学思想，激起学生的数学兴趣和探索欲。另外，还要引导学生“善于学”，善于联系平时的生活经验，以及所学的知识进行迁移，如，本堂课对教材进行创新处理，让学生在等式和一元一次方程的解及其解集的基础上类比学习。在小学就已经会利用天平情境分析，用等式刻画生活中存在的等量关系。在这基础上进行设计，天平倾斜，引出不等式刻画生活中不等关系。同时借助一元一次方程的解类比学习不等式的解及其解集的概念。最后，通过精选练习让学生“灵活用”。

一、“知其源”——教材分析

本节是《9.1.1不等式及其解集》，属于第九章《不等式与不等式组》中《9.1不等式》第一课时。包括不等式、不等式的解、不等式的解集、解不等式四个概念、“>、<、≥、≤、≠”五种不等号，列不等式、写出简单的不等式的解集、解集的几何表示方法三个基本技能。渗透符号意识，类比思想、数形结合思想以及建模思想、集合思想。其中概念是基础，解集的几何表示方法是核心技能。

同时本节课是学生在学习了一元一次方程和二元一次方程组的概念、解法及其应用后面临的一个新问题，不等式从某种程度上讲是等式的延伸，而在此之后，学生要学很多知识，比如，不等式的性质、一元一次不等式组、二次函数及方案设计等问题都要用到本节课的内容。因此，本节课的内容在整个中学数学起着承前启后的作用。

（一）数学文化“不等号”的由来

为了寻找表示不等关系的符号，多少年来，数学家们绞尽了脑汁。首先是法国的数学家日腊尔于1629年在他的《代数教程》中用“ff”表示“大于”，用“§”表示“小于”，如a大于b记作“affb”，a小于b记作“a§b”。其间，还有不少数学家提出了各种表示“大于”或“小于”的符号，但都由于这些符号书写起来十分繁琐、意义不够明晰，很快都被淘汰了。只有英国数学家哈里奥特在1631年创用的“>”表示“大于”，“<”表示“小于”，由于方便简捷，被延续下来，就是现在通用的大于号和小于号，如a4。

二、“善于学”——摘教学设计片段

活动一：借助“中小衔接”，引入课题

教师：幻灯片呈现生活中的数量间的相等和不等关系。学生举例说明生活中存在的不等关系。

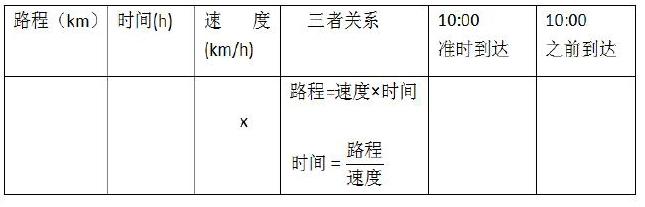
如图1，天平左盘放2个红球，右盘放1个5g砝码，天平倾斜，设每个红球的质量为 g，

（1）如何用含 的代数式表示天平左盘中两个红球的总质量？

（2）观察图1，你发现了什么关系？你能说明这是什么关系吗？

（3）如何用数学符号来表示天平左右两边代数式的数量关系？

设计意图：渗透“类比”思想，培养学生观察能力、表达能力，培养学生的符号意识.

活动二：教材改编——学生是主角

情境二：问君可知，车速几何？

问题（1）某天早上，七年级2班全体同学乘坐一辆匀速行驶的汽车8：00从学校出发到距离学校100千米的地方参加研学活动，要求在上午10：00点准时到达，车速应满足什么条件？请利用方程有关知识求解。

解：设车速为x千米/小时，可列方程：____________________________。

问题（2）如果要求在中午12：00点之前到达，车速应满足什么条件？

问题探究一：不等式的解

①方程的解：使方程左右兩边相等的未知数的值叫方程的解。

②实际意义背景出发：当车速是49千米/小时时，能否准时到达？

③填表：发现使不等式 成立的数有一个共同的名字，这个名字是

思考：类比方程的解的定义，请给不等式的解下定义。

设计意图：教学“不等式解（集）”等内容时，学生已经对“一元一次方程”有所感知，对“方程的解”有所体验。在此基础上，可以引导学生自觉地通过类比正迁移，探究相关内容。学生在原有知识的基础上自主生成新的知识，学习结果是牢固深刻的。因为这合乎知识的逻辑发展，符合学生的认知规律，正体现如何引导学生“善于学。”

问题探究二：不等式的解集

思考：由探究一知： 是不等式 的一个解。请问： 的解集是 吗？

① 的取值是否能让不等式 成立？完成表格，填写“成立”或“不成立”

②从表格中发现，不等式 的解还有吗？有多少个？

③从表格中发现，不等式 的总是成立的 要满足的条件是

设计意图：借助验证、归纳，引导新的认知冲突，借此，以小组讨论，合作交流，让学生充分发表意见，初步体会这一特征，既与方程的解有共同之处，又不同于方程的解，既与不等式的解有联系，又与不等式的解有区别，引出不等式的解集的必要性并理解不等式的解集的含义，从而突破难点。

三、“灵活用”——摘教学设计片段，联系生活构建不等模型

例2，每年5月第二个星期日是母亲节，母亲节是一个感谢母亲的节日，母亲们在这一天通常会收到礼物。忘忧草（又叫萱草花）被称作母亲花。唐朝诗人孟郊曾作诗“萱草生堂阶，游子行天涯，慈母倚门堂，不见萱草花”。这一天，本班有一位同学按八折买了2束忘忧草作为母亲节礼品，付费超过16元。若设每束忘忧草的标价为 元，你知道每束忘忧草的标价吗？

设计意图：体会不等式是解决实际问题的有效工具，同时对学生进行感恩教育的“德育渗透”，帮助学生感受“中华民族的传统美德，百善孝为先”文化。

四、基于实际教学活动思考与反思

（一）“知其源”——重教材，引文化

从教材出发，通过类比思想，由学生熟悉的等量关系模型方程出发，突出知识产生的必要性，让学生知道数学知识点的内在联系。通过“不等号由来”课后阅读，感受数学博大精深文化，通过渗透数形结合思想，突出方法的来龙去脉，让学生理性认识数学方法的合理性。结合学情对教材灵活处理改编，有意识、有计划、有条理地设计问题，形成认知冲突，符合学生的认知规律，注重知识点形成的过程，突出了数学教学的探索性，从而更好地体现数学知识的生成性，促使学生始终处于“疑”的状态，从而积极思维。

（二）“善于学”——善类比，巧迁移，学思想

章建跃说过，一个处于核心地位的中学数学概念是中学数学知识结构中的联结点，由其反应的数学思想方法是联系数学知识的强力纽带。夸美纽斯在《大教学论》中指出“如果不教明概念，便是教的不好的。”教学中应让学生明确：概念在生活中的实际背景是什么？——为什么引入这一概念？——如何建立这一概念？——学习这一概念有什么用？即，解决概念学习的“从哪里来，到哪里去”的问题。正如《全日制义务教育数学课程标准》指出：义务教育阶段的数学课程，其基本出发点是促进学生全面、持续、和谐的发展。它不仅要考虑数学自身的特点，更应遵循学生学习数学的心理规律，强调从学生已有的知识经验出发，让学生亲身经历将实际问题抽象成数学模型并进行解释与应用的过程，进而使学生获得对数学理解的同时，在思维能力、情感態度与价值等多方面得到进步和发展。

教学中，可从以下三个角度去引导学生“善于学”。如联系概念的现实原理引入新概念;从具体到抽象引入新概念;用类比的思想方法引入概念。如“不等式的解与不等式的解集”的概念引出、“用数轴表示不等式的解集”合理性与必要性的探讨，以及使用表格分析问题，内容设计都是为激发学生已有知识的迁移，渗透数学思想做铺垫。

（三）“灵活用”，精选练习，建构生活与数学的联系

一方面，借助信息技术的融合，要“灵活用”学生的作品展示，才能有更好的生成，适当追问及顺水推舟等。另一方面，通过设置题型多样的练习（填空、选择、计算、读图、开放题），且梯度明显，从基础概念辨析到巩固练习再到含参数的能力提升等。题量合理，梯度呈现使不同学生都获得成功体验，针对性强，可见力争减负不减效果。在教学过程，进行德育渗透，通过例题2的设置，不仅达到学生建立不等模型的效果，将生活问题转化为数学问题，同时进行母爱感恩教育。

参考文献：

[1]唐琦.初中数学概念课型教学的实践与思考[J].中学数学研究，2018（1）.

[2]施俊进.“单元在建构”章节起始课教学的实施智慧——不等式及其解集教学实践与反思[J].中学教育教学，2017（11）.