基于IPSO睧LM的电磁供暖室内温度预测

王航 王盛慧

摘 要：为克服电磁供暖系统对用户室内供暖时存在的温度滞后性，本文提出一种改进粒子群优化算法（IPSO）优化的ELM，用来对室内下一时刻的温度进行预测。该算法完善了PSO易跳过最优解、易陷入局部最优解以及收敛时间长等问题，然后分别用IPSO和PSO对ELM模型进行优化，建立基于IPSO-ELM和PSO-ELM的电磁供暖室内温度预测模型。

关键词：电磁供暖;温度预测;粒子群算法;极限学习机

在电磁供暖室内，供暖温度存在着滞后性[1]，建筑物蓄热性能、室外温度及历史温度等因素都会影响室内下一时刻的温度。故能否建立良好的室内温度预测模型的对后续电磁供暖系统的控制性能的好坏至关重要。在对电磁供暖室内温度的影响因素进行分析之后，明确ELM预测模型的输入输出变量。然后再分别用PSO和IPSO优化ELM的连接权值以及隐含层阈值。最后通过仿真验证了IPSO优化的效果较好。

1 ELM模型

ELM是由新加坡的著名学者黄广斌[2]在2004年所提出，并用来解决传统BP神经网络训练时间长、较易陷于局部的最优解以及对参数的选择苛刻等问题的一种新的前馈型神经网络算法。ELM与BP神经网络的不同之处在于其连接权值和隐含层阈值是由算法随机生成的，故只要确定隐含层中神经元的数目就可以进行训练学习，操作十分方便，泛化能力比较强。

2 基于IPSO的ELM优化

早在1995年，美国的Kennedy和James Eberhart就提出了粒子群算法这一概念。他们是在Frank Heppner鸟类模型建模与仿真取得了一定成果之后，并以此为基础，才共同提出了粒子群算法（PSO）。该算法在较少的参数设置量时就具备较强的寻优能力和收敛速度，因此经常被应用于各优化领域。

PSO是利用各个粒子对最佳的地点进行搜寻，然后经不断地迭代寻找得到全局最优解的过程。每个粒子的地点都可以用一个相应的适应度函数来表示，并且各粒子运动的方向和距离可用其保有的速度来表示。在整体的迭代过程中，利用個体的最优极值以及全局的最优极值来不断地进行更新。个体的最优极值指的是个体在进行一定的迭代次数后所获得的最佳地点，全局的最优极值指的是整个种群通过一定迭代次数后所获得的最佳地点。将粒子群速度和地点都用维数为S的向量进行表示，便可得到其迭代公式如下：

3 仿真结果分析

3.1 输入输出变量的选取

电磁供暖室内的温度存在着大惯性与大滞后性，并且与室内外温度、供回水温度及温控器状态等因素有关，综合上述因素本文将N-T刻室内温度、N时刻室内温度、N时刻温控器状态及N时刻供回水温差作为输入变量，N+T时刻室内温度作为输出变量。

3.2 试验数据采集选取

本文对某栋电磁供暖居民楼进行数据采样，每30分钟采样一次。为了获得全面的样本，本文从供热平台获取了2019年1月6号00点00分～1月11号23点30分的总计288组数据，并把前230组数据作为模型的训练样本，把后58组数据作为模型的测试样本，然后分别用IPSO-ELM和PSO-ELM进行预测试验。学习因子c1，c2取为1.5，迭代次数为100次，种群规模为50，隐含层神经元个数为9，最大、最小权值分别取为0.8、0.4，并采用S型函数作为激励函数。

3.3 试验对比分析

前230组训练集通过IPSO-ELM和PSO-ELM训练输出的室内温度值与实际在供暖平台获得的室内温度值能够很好的拟合，其拟合曲线如图1所示，由图可知，两种模型的拟合度均在合理范围之内。经过计算知IPSO-ELM的均方误差（MSE）为0.0303，PSO-ELM的均方误差（MSE）为0.0102，则IPSO-ELM模型的拟合程度比PSO-ELM模型略高些。

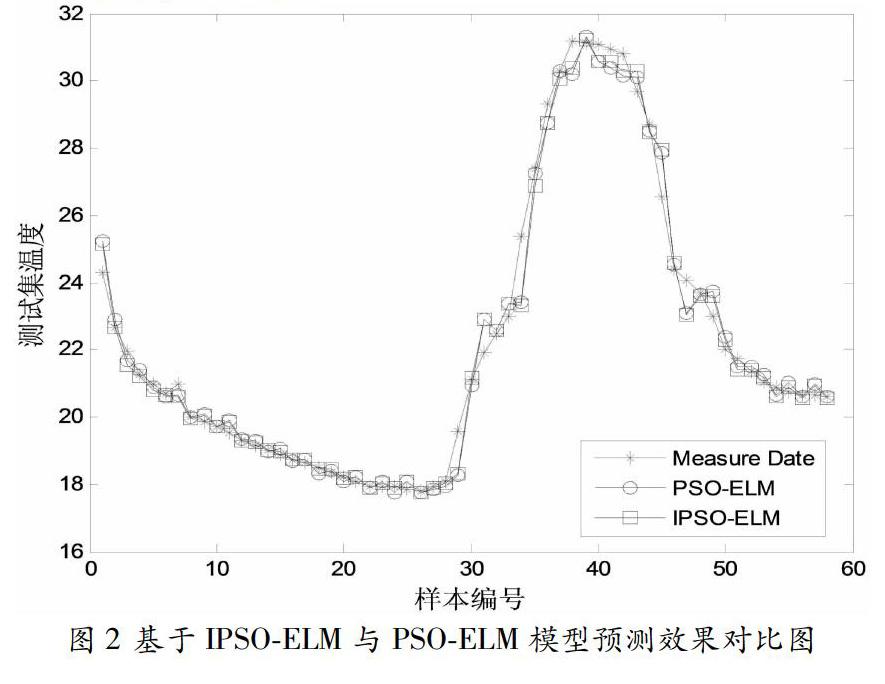
利用前230组训练集训练之后IPSO-ELM模型和PSO-ELM模型再分别对后58组测试集温度进行预测，得到如图2所示的IPSO-ELM和PSO-ELM的实际值与预测值的对比图，由图2可知，两种算法所预测的电磁供暖室内温度值的变化趋势与实际电磁供暖室内温度值的变化的趋势基本相同，且IPSO-ELM所预测的温度值与实际温度值更加接近，两种算法的预测误差对比如图3所示。

由图3可知，虽然两种算法在预测温度值上都存在一定的误差，但是IPSO-ELM预测准确度要高于PSO-ELM。

通过以上三项对比可知，IPSO确实对PSO进行了优化，IPSO-ELM模型比PSO-ELM模型更适合对室内温度进行预测。

4 结语

本文为对电磁供暖室内温度进行预测，提出了一种IPSO对PSO进行优化，并基于ELM对IPSO-ELM和PSO-ELM模型进行对比验证，试验结果表明IPSO-ELM预测模型的温度预测误差更小，具有更好的预测能力，能够胜任电磁供暖室内对下一时刻温度的预测要求，为后续电磁供暖控制系统的设计奠定了基础。

参考文献：

[1]李康吉.建筑室内环境建模、控制与优化及能耗预测[D].浙江大学，2013.

[2]穆冀里，蒋武锋，董建君，等.纳米铁粉的制备方法研究[J].粉末冶金工业，2014（02）：37-41.

[3]陈恒志，杨建平，卢新春，等.基于极限学习机（ELM）的连铸坯质量预测[J].工程科学学报，2018（7）：815-821.

作者简介：王航（1995-），男，汉族，山西临汾人，硕士研究生，电气工程专业。

*通讯作者：王盛慧（1976-），女，汉族，吉林长春人，硕士研究生，教授，电气工程专业。