丰富活动经验 提升度量素养
——以“面积单位”一课教学为例
2020-07-06陈金飞
陈金飞
(江苏省启东实验小学)
“面积单位”这部分内容属于《义务教育数学课程标准(2011年版)》“空间与图形”领域中“测量”的内容。在学习此内容之前,学生已经在二年级上册认识了长度单位,建立了长度单位的表象经历、体验了“采用统一的长度单位”的探究过程。从知识系统层面而言,“面积单位”的学习是学生从一维空间和二维空间走向三维空间的重要一环。与长度、面积、体积相关联的知识虽然分布在不同的年级,但他们是同一类纵向的、具有内在联系的知识。教学中,教师应把这一类课进行关联思考和整体设计,帮助学生整体建构知识体系,这对于学生有意义地掌握知识、形成能力、达到“四基”的要求具有重要意义。
一、经历单位标准的统一过程,渗透度量意识
统一性是计量的本质特性。测量长度需要一把“长度尺”,因为“长度尺”上有统一的长度单位。测量面积同样需要一把统一标准的“面积尺”,那就是“面积单位”。所以我们在教学时,要运用多种方式,让学生体会统一“面积单位”的必要和价值。由于学生在学习“面积的意义”时发现,两个平面图形中,正方形格子数占得多面积就大,因此不妨设计一个引发认知冲突的情境,让学生产生用统一的标准去比较面积的心理需求——因为测量的标准量不相同,所以不能由此来判断面积的大小,应该用大小一样的正方形去度量才合理。在此基础上,使用具有统一标准的国际面积单位便成了大家的共同需要,接着再教学面积单位也就水到渠成了。
师:下面两个长方形哪个面积大?

生:我觉得第一个长方形面积大。
生:我觉得第二个长方形面积大。
师:看来凭直觉观察两个图形,无法判断两个图形哪个大。有什么好办法来比较这两个图形的大小?
生:可以移动其中的一个图形,让两个图形重叠在一起。(多媒体演示)

师:谁来说说哪个图形的面积大?
师:看来通过观察、重叠,均无法比较出两个图形面积的大小,怎么办?
生:我们可以找一个标准量分别量一量两个图形的大小,再进行比较。
师:谁听明白了他的想法?
生:我听懂了他的想法,就是用一个小的图形做面积尺去量这两个图形。
师:说得真好,测量长度创造了“长度尺”,测量面积也需要一把合适的“面积尺”。请你设计一个形状和大小都合适的测量标准,比较这两个图形的大小。
生:我想把“面积尺”设计成圆形。
师:我们请出圆形“面积尺”,大家看看有什么问题?
生:测量的时候我发现有很多地方有空隙,空隙地方的面积没有测量进去。
生:我想把“面积尺”设计成长方形。
师:我们请出长方形“面积尺”,大家看看有什么问题?
生:测量时我发现长有剩余,宽正好。
生:那如果设计成正方形,不就正好了吗?
师:是不是这个意思?(把面积尺设计成小正方形,多媒体出示下图)

师:现在你能确定哪个长方形的面积大了吗?
生:第一个长方形的面积大。
师:是不是含有21个方格的图形面积一定比含有20个方格的图形面积大?
生:不一定。如果方格不一样大就不一定。
师:你对数学的感觉真好。一起观察这两个图形谁的面积大?

师:还有不同的想法吗?
生:含有21个方格的图形面积还可以等于含有20个方格的图形面积。
师:面对大小不同的图形,怎样才能正确判断图形面积的大小?
生:用相同大小的图形去测量。
师:用同样大小的正方形去测量的话,测量的标准就得到了统一,这个统一的标准就是我们要研究的面积单位,也就是大家创造的“面积尺”。
二、经历单位表象的建构过程,发展度量意识
表象的建立,依赖于操作。操作是一种特殊的认知活动。小学生动手操作时,总是在视觉、触觉、运动觉协同感知事物的同时,就以内部语言悄悄地展开了思维。他们在操作时必须同时思考如何触摸,如何摆放,如何移动……而在操作中获得的形象和表象,又及时推动着他们进行分析、综合、比较、抽象、概括,使他们深刻地理解知识的本质意义。“面积单位”的教学,操作是必不可少的一种活动。因此,教师在教学时要把握好操作的时机,只有有意识地放慢学生获得结论性结果的过程,我们才能真正地落实“过程性目标”的要求。我们不仅要让学生建立面积单位的清晰表象,更要让学生经历体验的过程。通过看一看、摆一摆、数一数、算一算、找一找、比一比六个环节,让学生头脑中的表象得到不断地调整与明晰,经历由肤浅到深刻、由粗放到精准的表象建立过程。学生从操作中感悟,从操作中理解,就能在正确建立面积单位表象的同时积累基本活动经验,发展度量意识。
师:像这么大的正方形面积是1平方分米。平方分米是国际常用的一个面积单位。(板书:平方分米)
师:举起桌上的1平方分米,仔细看看它的大小。用数学语言来描述一下:多大的正方形,面积是1平方分米?
生:边长是1分米的正方形,面积是1平方分米。
师:你真棒,能抓住边的长度来描述正方形的大小。我们借助直尺来量一量正方形的边长。
生:面积是1平方分米的正方形,边长是1分米。
师:同桌互相说说1平方分米是怎么规定的?
师:平方分米还可以用符号dm2(板书:dm2)表示。看清楚1平方分米的大小,闭上眼睛记一记。睁开眼睛,找一找生活中哪些物体的面大约是1平方分米?
生:开关的面。
生:粉笔盒的正面。
生:小的记事本的上面大约是1平方分米。
师:大家的观察力真强。其实在我们的身上就藏着一个接近1平方分米的面,看谁最先发现。
生:我们的手掌面。
师:你太厉害了,一下子就找到了。感谢这位同学。伸出你的手,用1平方分米和你的手掌比一比。有了这个面积单位,今后我们估计一些物体的面的大小时就方便多了。
师:估计一下我们的课桌面面积大约是多少平方分米?(学生纷纷用手掌面去测量)
生:30平方分米,24平方分米,28平方分米。
师:到底是多少?用1平方分米的面积单位,同桌合作测量课桌面的面积。
操作指南:
(1)量一量:用1平方分米测量课桌面的面积。
(2)说一说:课桌面的面积是多少平方分米。
(一组学生上黑板测量磁性课桌面)
师:有结果了吗?请上黑板操作的这组学生汇报一下测量的结果。
生:我们一行摆6个,摆了4行,一共摆了24个1平方分米,测得的课桌面的面积是24平方分米。
师:解释得多好呀。铺满课桌面,一共用了24个1平方分米,课桌面的面积就是24平方分米。
师:有不同的测量方法吗?
生:我们没有铺满,只摆了一行一列。一行是6个,一列是4个,铺满就是4个6,课桌面的面积是24平方分米。
师:大家听明白他的解释了吗?真了不起。他们沿着长摆了6个,沿着宽摆了4个,大家想象一下,铺满的话要用——
生:24个1平方分米。面积就是24平方分米。
师:刚才我们认识了“平方分米”,用这个面积单位测量了课桌面的大小。如果要测量一块橡皮上面的面积,你觉得选用平方分米作面积单位合适吗?
生:我觉得可以的。用橡皮去摆1平方分米的图形,看一共摆了几块橡皮。
生:我觉得他的方法是错误的。他把橡皮作为面积单位来测量,而老师要我们用平方分米这个面积单位来测量橡皮。
生:即使我们同意他的方法,也无法知道橡皮的一个面是多少平方分米。
师:看来用平方分米来测量橡皮的一个面的大小不合适。那怎么办呢?同学们有什么好的建议和想法吗?
生:我们可以创造一个比平方分米小的面积单位。
生:对,可以创造面积单位——平方厘米。
三、经历单位变式的体验过程,形成度量素养
在“面积单位”的学习中,学生选择合适的面积单位时容易发生错误,因为这并不是三个面积单位的简单选择,它需要经历表象提取、单位假设、参照比较、排除推断等综合思考的过程。学生在解决这类问题时,多数是凭着自己的感觉去推断,比较大的物体表面选择较大的面积单位,反之选用较小的面积单位。所以我们在教学时,要注意引导学生建立相关参照物的表象,指导学生进行推断,既要考虑数据的大小,又要关注单位的不同。要引领学生经历“建构—调整—再建构”螺旋式递进的过程。在教学中,要有意识地运用变式练习,设计“我来猜、我来估、我来算”等活动,让学生在不同情境中感悟同一个对象,逐步聚焦、归纳,使体验得到升华。如在“我来算”环节中可以澄清学生头脑中可能存在的错误认识——1平方厘米的图形只能是边长1厘米的正方形。同时,这也是为计量非长方形的面积作铺垫,为将来平行四边形面积计算公式推导作孕伏,可谓“走一步,看两步,想到第三步”,做到前有铺垫,后有呼应,帮助学生形成良好的认知结构,形成度量素养。
【我当猜谜师】
师:听清楚要求,根据所给数据,猜猜谁的大小最接近这个数据。
第一组:6平方厘米。
(1)橡皮上面的面积;(2)教室地面的面积;
(3)指甲面的面积。
生:指甲面的面积。
生:我反对,指甲面的面积大约1平方厘米,应该是橡皮上面的面积。
师:和他想法一样的请举手。为什么不是教室地面的面积?
生:教室地面的面积应该用平方米作单位,6平方厘米太小了。
第二组:4平方分米。
(1)邮票的面积;(2)数学书封面;
(3)多媒体幕布。
生:数学书封面面积大约4平方分米,用手掌面去量一下就知道了。
师:邮票的面积更接近4( )?
生:邮票的面积更接近4平方厘米。
师:多媒体幕布的面积接近4( )?
生:多媒体幕布的面积接近4平方米。
师:真了不起。看来大家对物体表面大小的直观判断能力真强。
【我当估量师】

师:一张银行卡的面积大约50( )。
生:一张银行卡的面积大约50平方厘米,不可能是50平方分米,因为1平方分米大约1个手掌面这么大。
师:那数学书封面的面积大约( )平方厘米。
生:200平方厘米。
生:1000平方厘米。
生:我觉得大约是400平方厘米。我们可以用这张银行卡作为标准量去度量,大约8张银行卡可以铺满数学书封面,所以我估计400平方厘米。
师:你的估算能力真棒,做到有根有据,把掌声送给他。
【我当计量师】(每小格表示1平方厘米)

师:观察这些图形,你有什么发现?
生:这些图形的面积都是1平方厘米。
生:即使不是正方形,面积也可以是1平方厘米。
师:你真了不起。我们用简练的数学语言来概括一下大家的发现。
师:下图的面积是多少平方厘米?(每小格表示1平方厘米)
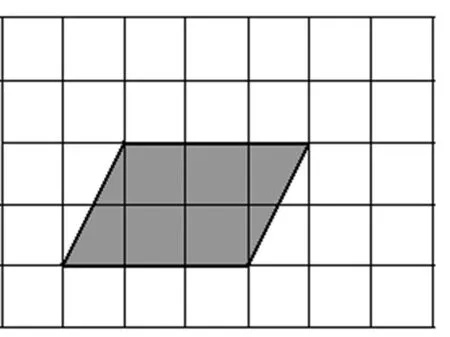
生:这个平行四边形的面积是6平方厘米。
师:说说你的想法。
生:把左边的两个不是整格的拼起来,把右边两个不是整格的拼在一起,一共6格,所以是6平方厘米。
生:我们可以用平移的方法,把左边的直角三角形平移到右边,拼成一个长方形,就可以数出来了。
师:这两位同学考虑问题的思路很清晰。把不是整格的转化为整格计算,第二位同学用平移的方法将平行四边形转化为长方形的来计算,真不愧是我班的“数学小博士”。
数学学习的过程应该是让学生自主探索知识、感受知识、体验知识的过程,这样形成的表象记忆深刻。课堂教学建立在学生充分感知的基础上,关注体验、关注思维、关注需要,才能深刻建构空间观念,发展学生的度量素养。
