冰雨环境下太赫兹波传输特性研究
2020-07-06周忆鑫杨晓帆刘小明
齐 涛, 周忆鑫, 杨晓帆, 甘 露, 刘小明
(1.安徽师范大学 物理与电子信息学院,安徽 芜湖 241002;2.安徽省智能机器人信息融合与控制工程实验室,安徽 芜湖 241002;3.电子信息系统复杂电磁环境效应国家重点实验室,河南 洛阳 471004)
关键字:THz波;衰减;粒子;Mie理论
太赫兹波(terahertz wave)是指波长在0.03mm-3mm之间的电磁波,所对应的频段为0.1THz-10THz。由于太赫兹波的波长位于微波和红外线之间,所以太赫兹波与微波、光波相比具有自己独特的性质。与微波通信相比,太赫兹波通信具有探测精度高、抗干扰能力强、通信容量大、波束窄、体积质量小等特点;与光通信相比,太赫兹波通信具有很好的穿透沙尘的能力、受气象和烟尘的影响小、具备全天候工作的能力等特点。
除通信外,太赫兹技术在遥感[1]、探测[2]以及雷达[3]等方面有着广泛的应用。这些应用中的一个关键问题是太赫兹波传输特性。空气中大多数的极性分子对太赫兹波有强烈的吸收,造成传输信号的衰减。此外,降雨和冰晶粒子等颗粒物对太赫兹波产生的吸收与散射也是不容忽视的。
国内外对太赫兹波传输特性进行了广泛的研究。例如,在国际电信联盟建议书ITU-R P.676-11附件2的等效高度模型中考虑了不同大气压力时350 GHz以下频率的路径衰减[4]。但此模型仅包含大气压,对不同的地区和季节而言并不准确。李海英[5]等人提出了包含温度和水蒸气的改进模型,并验证了结果。Ishii[6]等人比较了96GHz-355GHz频率下降雨强度高达25mm/h的雨衰减。为了将这些结果应用到无线通信领域中更宽的波段,他们构建了一种1GHz-1000GHz频段的雨衰减模型。Yang[7]等人在计算冰晶粒子单次散射特性时,将冰晶粒子尺度范围设定为过于宽泛的2μm -10000μm。
但是,在目前的公开文献中,尚未发现对冰雨混合情形的系统性研究工作。有鉴于此,本文利用Mie理论研究不同强度降雨、不同粒子尺寸冰晶等两类情形下太赫兹波的消光系数,结合雨滴和冰晶粒子的谱分布,研究不同强度降雨、不同粒径冰晶及冰雨混合等几种环境下太赫兹波的传输特性。
1 基本理论
1.1 雨滴的物理特性
雨的尺寸分布对太赫兹波传输会产生明显的影响。雨滴谱是描述雨滴尺寸分布的主要方法,它是指在不同降雨率的条件下,雨滴粒径大小的分布状况。目前,雨滴谱可以通过雨滴谱仪测量得到,通过测量一定时间内的降雨,根据统计方法得到雨滴尺寸分布,再通过建模,得到数学模型。目前的雨滴谱模型有Laws-Parsons模型[8],Marshall-Palmer模型[9],Joss模型[10],对数-正态分布模型[11]及gamma模型[12]等。
实测的雨滴谱分布略有不同,在这里使用Marshall-Palmer分布:
N(D)=8000e-0.41R-0.21D(m-3mm-1)
(1)
式中:R为降雨率,D为雨滴粒子的直径,N为单位体积单位直径的雨滴数。
除雨滴粒子的分布特征外,雨滴的介电常数是影响其散射特性的另外一个关键参数。由于水是构成雨滴的主要成分,因此需要先研究水的介电常数以更好的计算雨滴的传输衰减。在Mie理论中,介电参数采用的是物质介电常数与空气介电常数之比。另外,由于它具有频率相关性,因此需要采用复折射率比来描述。由于水的吸收特性比较明显,因此复折射率可表示为:

(2)
式中:λ为入射波波长,n、n1和n2分别是复折射率、复折射率实部与虚部。另外,根据复折射率与介电常数的关系可知,εr、ε′和ε″分别是复介电参数、复介电参数实部与虚部。
Ray[13]经验公式是用于描述水的介电常数的常用公式之一。它是在实验结果的基础上,通过拟合数学模型得到的与实验结果比较相符的经验性公式,即:

(3)
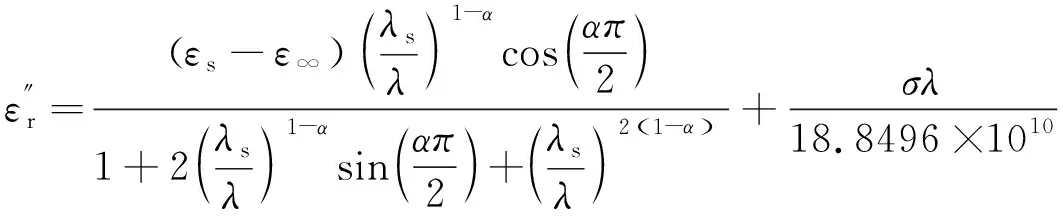
(4)
式中的参数为:
σ=12.5664×108
(5)
εs=78.54[1-4.579×10-3(t-25)+1.19×10-5(t-25)2-2.8×10-8(t-25)3
(6)
ε∞=5.27134+2.16474×10-2t-1.31198×10-3t2
(7)
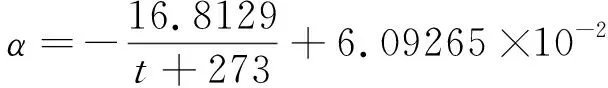
(8)

(9)
此处,εs是水媒质的静相对介电常数,ε∞是高频(近光波段)相对介电常数,λ是入射波波长,而t为温度(℃)。
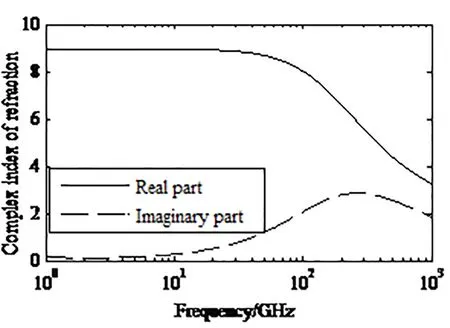
图1 水的复折射指数分布图Fig.1 Complex refractive index distribution of water
采用该方法计算出雨滴在1GHz-1000GHz波段的复折射指数如图1所示。
1.2 冰粒子的物理特性
在计算冰对太赫兹波传输的影响时,同样要用到冰晶谱,冰晶谱分布主要有对数正态分布、伽马分布、双峰伽马分布、幂指数分布等[14]。其中,伽马分布[15]是辐射传输模型中常用的冰晶粒子尺寸分布:
N(D)=N0Dμe-βD
(10)
其中N0是滴谱的浓度,β是斜率,D为粒子最大尺度,μ是形状参数取值范围0-2。
另外,为计算冰对太赫兹波传输的影响,还需要冰的复折射指数。Ray[13]在广泛收集实验的数据的基础上,构建了冰的复折射率的经验模型。该模型适用于-20℃到0℃的冰,其表达式为式(3)和式(4),但其特征参数为:
ε∞=3.168
(11)
α=0.288+0.0052t+0.00023t2
(12)
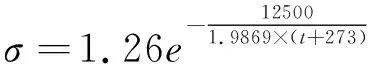
(13)

(14)
εs=203.168+2.5t+0.15t2
(15)

图2 冰的复折射指数分布图Fig.2 Complex refractive index distribution of ice
采用该方法算出冰在1GHz-1000GHz波段的复折射指数。图2给出了该波段的复折射指数分布。
2 冰和雨的太赫兹波的衰减特性
在降雨或冰雹环境中,太赫兹波的传输衰减,和粒子的尺寸分布、单个粒子的消光截面等因素有关。因此,在已知粒子的尺寸分布的条件下,太赫兹波的衰减[16]可表示为:

(16)
式中:衰减系数A的单位dB/km,r为水滴半径,n(r)为水滴的尺寸分布,Qe为单个水滴的消光系数。通常情况下,雨滴半径在0.01mm-4mm之间,式(16)表明总的衰减率为单个粒子衰减率的叠加。
3 计算结果及分析
图3是雨的散射截面随频率的变化图,由图可以看出雨的消光系数主要由雨的散射导致,消光系数等于散射系数加吸收系数。
图4为不同降雨率的特征衰减随频率的变化关系。图4给出了降雨率为12.5mm/h、25mm/h、50mm/h、100mm/h时环境温度为25℃条件下的雨的特征衰减。

图3 雨的散射截面图
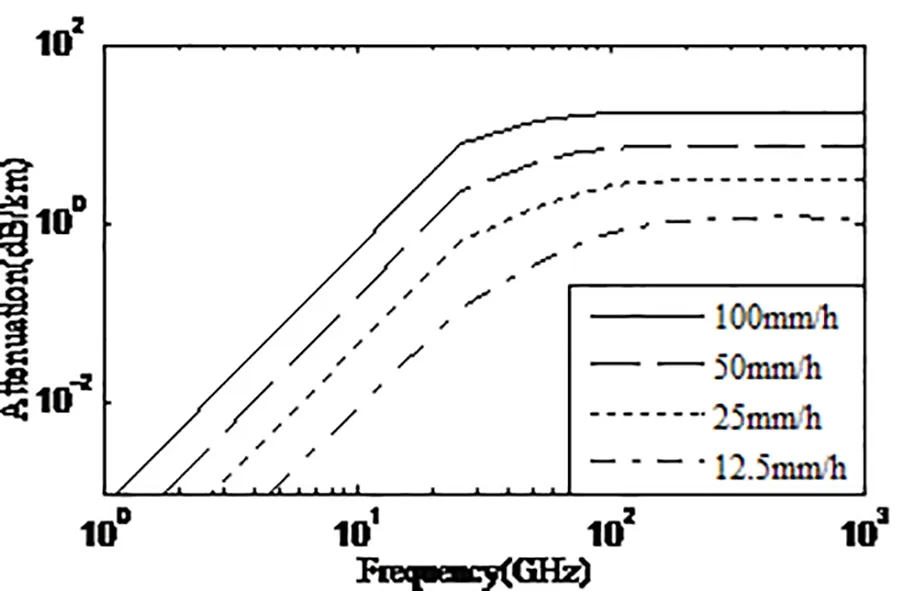
图4 雨特征衰减与频率的关系
Fig.4 The relationship between rain characteristic attenuation and frequency
从图4中可以看出太赫兹波在降雨中的衰减与降雨率有关,降雨率越大,衰减越大。同时衰减与频率成比例增加,然后达到一个峰值后,在高频段衰减开始缓慢减小或者基本保持不变。
冰晶粒子的散射截面如图5所示,从图中结果可看到,冰晶的散射是引起冰晶粒子消光的主要原因,另外,吸收系数随频率的增加而增加、消光系数同样是散射系数和吸收系数之和。图6为不同形状参数的冰晶粒子的特征衰减随频率的变化关系。图6给出了形状参数分别为0、1、2(指圆柱形冰晶的长与直径的比值分别为4、2、1)时冰的特征衰减。
从图6中可以看出冰晶粒子的衰减与形状参数有关系,但形状参数对衰减的影响不大。同时特征衰减与频率成比例增加,然后达到一个峰值,在高频段衰减开始减小或者保持不变。

图5 冰晶粒子的散射截面图

图6 冰晶粒子的特征衰减与频率的关系
Fig.6 The relationship between characteristic attenuation of ice crystal and frequency

图7 冰雨的特征衰减与频率的关系Fig.7 The relationship between the characteristic attenuation of ice rain and frequency
图7是在冰晶粒子的形状参数μ=0时,降雨率为12.5mm/h、25mm/h、50mm/h、100mm/h时的冰和雨的衰减叠加的结果。可以看出当太赫兹波在冰和雨的混合环境中传播,随着频率的增大衰减逐渐增大,对于太赫兹通信而言,冰和雨对太赫兹波的衰减会严重影响通信的质量。
4 结论
本文采用Mie散射理论、粒子分布模型分析、雨和冰晶粒子的介电特性,研究了太赫兹在雨和冰晶环境下的传输特性,比较了不同强度的降雨对太赫兹波产生的衰减以及不同形状参数的冰晶粒子对太赫兹波传输的影响,分析了雨和冰晶粒子的特征衰减与频率的关系。结果表明雨对太赫兹波造成的衰减比微波、毫米波段的衰减严重。雨造成衰减随着降雨率的增大而增大。同时雨的特征衰减并不是随频率单调增加,而是先增加后缓慢减小或基本不变。最后,将雨的衰减与冰晶的衰减叠加得到混合环境下的衰减。
