流行性传染病传播系统的奇摄动解
2020-07-06莫嘉琪陈怀军
莫嘉琪, 陈怀军
(安徽师范大学 数学与统计学院,安徽 芜湖 241003)
引言
流行性传染病为生态医学等学术界广为重视和关注,它给人类的生活和生产建设带来了很大的影响和灾害。在古罗马帝国时期发生的Antonine瘟疫,由于广泛地流行,导致入侵者乘机而入,以致罗马帝国覆灭[1]。AIDS传染病直到二十世纪底,全球感染上HIV病毒人数达到近6千万人,涉及二百个地区和国家,死亡人数超过二千一百万人[2]。 另外,有关SARS病毒,疯牛病,禽流感和最近发生的新冠病毒等流行性传播的各种传染疾病,在世界各地不断地在发生,对于这些情况,已是各国生态学者的十分关心的问题。
对流行性传染病传播的研究和讨论,一般只是以一些单纯地观察和简单的统计数据来做出判断,但它不能完全反映传播现象的本质。当前对流行性传染病的研讨,已开始将它归化为数学物理上的动力学方法[3-6]。也就是将它转化为微分方程系统动力学的模型,再用数学的解析分析和利用大数据技巧等方法来得到相应问题的渐近解,并将得到的数据结果来分析,最后从医学,生态学和数学物理等交叉学科的理论和方法来得出它的动态规律。这种方法已成为当代传染病生态学研究的主流。本文提出了一类非线性流行性病毒传播的系统模型,利用解析理论和方法来探求流行性传染病的传播规律。
非线性微分方程系统模型当前已有许多科学工作者做了许多的研讨[7-12],作者团队也曾研讨了一些对非线性相关的问题的模型[13-22],本文是用奇异摄动理论的解析理论方法来讨论一类常见的传染病病毒模型。
1 病毒传染群体传播模型
现讨论如下的传染病传播群体的模型,它是传染病传播群体关于人口的出生率与自然死亡率变化相关的生态系统初值问题[5,6]:
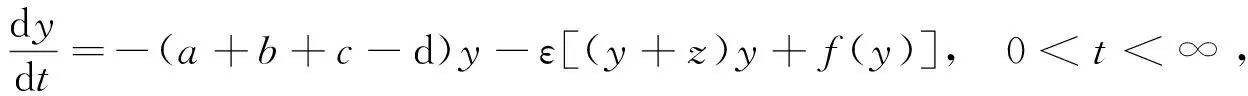
(1)

(2)
y(0)=A,
(3)
z(0)=B,
(4)
上述y为受感染者人数的相对值,z为感染者恢复而移出人数的相对值,a为传播疫区人数的死亡率,b为传播疫区人数的出生率,c为传播疫区人数的恢复率,d为传播疫区人数的传染率,e为传播疫区人数的再次被感染率,f(y),g(z)分别为感染者人数的相对值和移出者人数的相对值由于外加因素引起的其它扰动函数,设它们是足够光滑的有界函数,A,B为常数,ε为摄动参数。系统(1)-(4)是一个生态动力学病毒传播的模型,我们用奇异摄动方法来求得该传染病毒传播系统模型的渐近解。
2 传播模型的外部解
现求模型(1)-(4)相应的外部解(Y,Z),设

(5)
将(5)式代入模型(1)-(4),合并εi(i-0,1,2,…)的系数。
由ε0的系数有

(6)
cY0-(b+e)Z0=0,
(7)
Y0(0)=A。
(8)
不难由(6)-(8)式得到
Y0(t)=Aexp (-(a+b+c-d)t),
(9)

(10)
由ε1的系数有

(11)
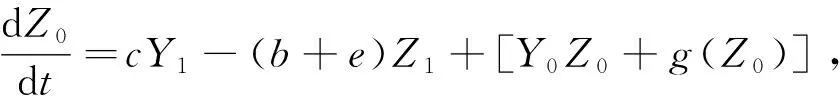
(12)
Y1(0)=0,
(13)
不难由(11)-(13)式得到

(14)

(15)
(11)-(15)式中的Y0,Z0分别由(9),(10)式表示。
同样,由εi(i=2,3,…)的系数相同的方法,可以依次求出Yi(t),Zi(t)(i=2,3,…),其表示式从略。

3 传播模型的初始层校正项
设生态系统初值问题(1)-(4)的解(y,z)满足

(16)
并设伸长变量τ为

(17)
将(16),(17)式代入初值问题(1)-(4)并考虑到已得到的外部解Y(t),Z(t),有如下初值问题:
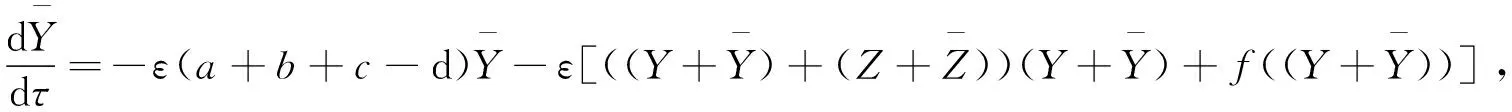
(18)

(19)

(20)

(21)
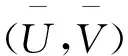
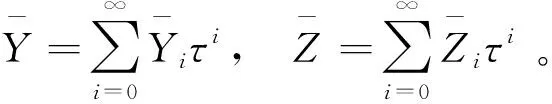
(22)
将(22)式代入初值问题(18)-(21),合并ε的同次幂项,由ε的零次幂的系数得

(23)
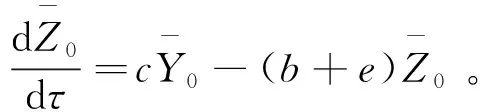
(24)

(25)

(26)
由初值问题(23)-(26)得解

(27)
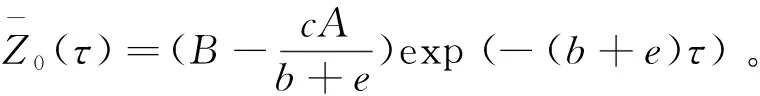
(28)


因此,由关系式(16),便得到生态系统初值问题(1)-(4)的奇异摄动解:

(29)

(30)
4 奇异摄动解的一致有效性
现在来证明生态系统初值问题(1)-(4)的奇异摄动解(29),(30)的一致有效性。
[定理]生态系统初值问题(1)-(4)的奇异摄动解(29),(30)在t∈[0,∞)上关于摄动参数ε是一致有效的渐近展开式。
[证明]首先在t∈[0,∞)上作辅助函数:
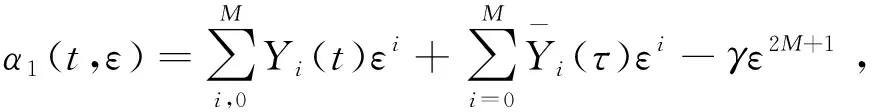
(31)
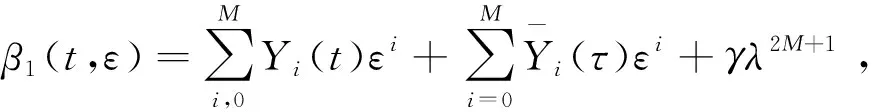
(32)

(33)

(34)
其中γ为足够大的待定正常数,M为任意的正整数。
由辅助函数(31)-(34),显然有
αi(t,ε)βi(t,ε),i=1,2,t∈[0,∞)。
(35)
考虑到(5)和(22)式,对足够小的ε,存在正常数D11使得
选取γ≥D11有
α1(0,ε)Aβ1(0,ε), 0<ε≪1。
(36)
同样,存在正常数D12,选取γ≥D12有
α2(0,ε)Bβ2(0,ε), 0<ε≪1。
(37)
由(31)-(34),(6),(11),(23)等关系式,并考虑到(5)和(22)式,对足够小的ε,存在正常数D21使得






(38)
同样,选取足够大的正常数γ,分别有

(39)

(40)
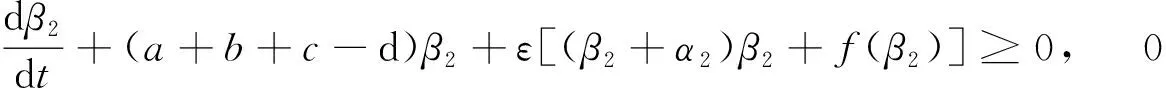
(41)
由上述得到的关系式(35)-(41),根据微分方程的比较定理得知
α1(t,ε)β1(t,ε), 0
(42)
α2(t,ε)β2(t,ε), 0
(43)
由关系式(42),(43)知,生态系统初值问题(1)-(4)的奇异摄动解(29),(30)在t∈[0,∞)上关于摄动参数ε为一致有效的渐近解。定理证毕。
5 举例
为简单起见,在模型(1)-(4)中,取无量刚参数a=b=c=e=1,d=0.5,A=2,B=0,f(y)=exp (-y),g(z)=exp (-z)。考虑如下一个非线性流行性传染病传播系统生态模型耦合系统初值问题:

(44)

(45)
y(0)=2,
(46)
z(0)=0,
(47)
设模型(44)-(47)的外部解Y(t),Z(t)为

(48)
由(9),(10)式
Y0(t)=2exp (-2.5t),
(49)
Z0(t)=exp (-2.5t)。
(50)
再由(14),(15)和(49),(50)式得

(51)


(52)
同样,可以继续求出Yi(t),Zi(t)(i=2,3,…),其具体的表示式在此从略。
于是生态模型耦合系统初值问题(44)-(47)的外部解Y(t),Z(t)为
Y(t)=2exp (-2.5t)
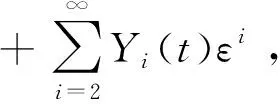
(53)
Z(t)=exp (-2.5t)
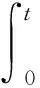

(54)
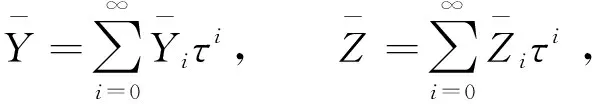
(55)
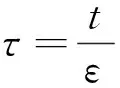
由(27),(28)式得

(56)

(57)
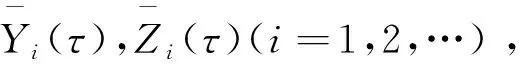

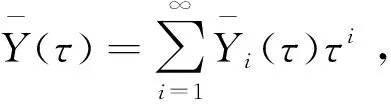
(58)

(59)
因此,便有生态系统初值问题(44)-(47)的奇异摄动解:
y(t)=2exp (-2.5t)

z(t)=exp (-2.5t)
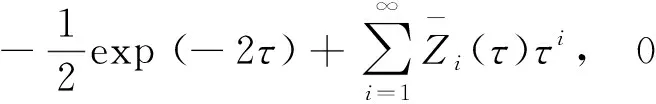
由上述计算的解析结果,取ε=0.8,对应的图形如图1,图2所示。

图1 精确解y和零次近似y0,一次近似y1,二次近似y2的比较
Fig.1 The exact solution compares with zeroth approximation,first approximation and second approximationy2

图2 精确解z和零次近似z0,一次近似z1,二次近似z2的比较
Fig.2 The exact solution compares with zeroth approximation,first approximation and second approximationz2
由图形可以看出,各次渐近解与模型精确解比较,当求得的渐近解的阶数越高时,越接近精确解。故得到的渐近解具有较好的近似度。
6 结论
流行病的传播是复杂的生态现象,人们要把它规化为基本系统的数学模型,并用近似的方法求出它的解。奇异摄动方法就是一个有效的方法。用本文得到的渐近解为基础,可以对流行病毒的传播规律作出预报,以便采取相应的措施来控制它。
奇异摄动方法是一个解析方法,它不同于用简单的数值模拟的求解方法。本方法得到解的解析表示式还能再进行各种解析运算,因此能够继续用解析运算来对其它相关物理量的各种性态作更深入的讨论。
