基于改进GNN的导引头DSP性能预测方法

岳 炯，吕卫民，苏宁远，胡文林

(海军航空大学， 山东 烟台 264001)

灰色神经网络(Grey Neural Network，GNN)的原理是将灰色系统理论和神经网络有机结合，主要应用于解决数据量较少的不确定性问题[1-3]。灰色系统理论是我国著名学者邓聚龙于1982年提出的一个采用数据生成，并从生成中寻找数学规律的边缘学科[4-5]。灰色系统理论的原理是通过对小数据量样本进行灰色生成，对小数据、不确定性系统进行处理加工，从中提取有价值的信息知识，发掘其中规律[6]。神经网络是一种人工智能新兴起的研究方法，具有大规模并行、分布式存储和处理、自组织、自适应和自学能力，特别是处理需要同时考虑许多因素和条件的、不精确和模糊的信息处理问题[7]，其中BP神经网络(Back-Propagation Neural Network)是误差逆向传播算法训练的多层前馈神经网络，是目前应用最广泛的神经网络。两种方法针对不同预测对象各有自己优点，灰色预测模型通常应用于规律趋势较强、波动不明显的预测问题，神经网络主要应用于规律无序、波动相差较大的时间序列[8-9]。

机载导弹导引头电子器件在长期贮存过程中，由于受到温度、湿度、机械振动以及电化学腐蚀等外界因素变化的影响，其内部材料性能也随之发生物理和化学变化，对应的性能参数也将改变，从而造成使用障碍，甚至失效[10]。在各种影响因素作用的环境下，电子器件失效的发生遵循一定规律，若能够准确掌握导引头电子器件失效规律，从而做到事故前预防，及时排除故障发生。GNN在电子器件性能分析及预测方面已有较为广泛的应用。例如，陈华平等人对电子产品性能评估方法现状、数学模型和加速实验的方法进行了分析，并介绍了灰色预测和神经网络预测方法的研究现状和发展前景[11]。祝德虎等人结合灰色系统理论和BP神经网络建立了灰色神经网络组合预测模型，对某型空舰导弹电子设备失效时间进行预测，结果显示预测精度高且实用性强，效果明显优于传统灰色预测模型[12]。

为此，针对导引头电子器件数据“样本少、信息不一致和偏差较大”等特点，本文开展基于GNN的导引头电子器件性能预测研究，对原算法模型进行适应性改进，以进一步提高预测精度和运算速度。

1 灰色GM(1,1)模型

1.1 传统灰色GM(1,1)模型

灰色GM(1,1)预测模型表达式为：

X(0)(i)+aZ(1)(i)=b

(1)

式(1)中：X(0)(i)为原始序列；系数a为发展系数；系数b为灰作用量；Z(1)(i)为白化背景序列。背景值z(0)=(z(0)(1),z(0)(2),…,z(0)(n))，其中：

(2)

式(2)中：α一般取0.5。设X(0)是非负序列，X(1)是X(0)的一次累加序列，Z(1)是X(1)的紧邻均值生成序列，则灰色微分方程可描述为：

(3)

其白化方程为：

x(0)(t)+az(1)(t)=b

(4)

也称影子方程。

采用最小二乘法，则离散型灰色微分方程x(0)(k)+az(1)(k)=b的参数列满足：

[a,b]T=(BTB)-1BTY

(5)

其中，

求得方程的解：

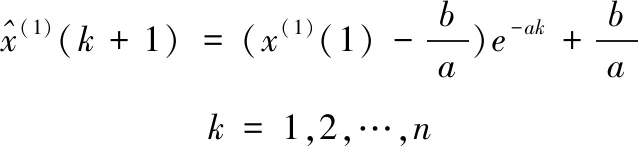
(6)

(7)

1.2 无偏GM(1,1)模型

在GM(1,1)指数序列建模过程中参数不可避免地存在偏差，为了消除GM(1,1)模型在原始数据增长过程中可能失效的问题，采取对参数进行修正的方法，生成无偏GM(1,1)模型(Unbiased Grey GM(1,1)，UGM(1,1))。UGM(1,1)同时也简化了计算过程中需要累减处理的环节，提高了计算速度。相对比传统灰色GM(1,1)，UGM(1,1)模型引入模型参数A和B，有：

(8)

由此可得到对应于原始数据序列的预测值模型为：

(9)

1.3 改进无偏GM(1,1)模型

对无偏GM(1,1)改进的常见传统方法有幂函数法和新陈代谢法。两种方法原理不同，幂函数法的原理是对序列数据分别求其二次方根，建立新的数据序列后再建模，能够有效提高数列的光滑度和解决偏差问题。新陈代谢法的原理是对原始样本补充新数据的同时，对原始样本中陈旧数据进行过滤，目的是使得改进后的数据序列的变化能够更好地适应运算模型，进一步提高运算精度。本文对无偏GM(1,1)模型进行改进采用幂函数法和新陈代谢法相结合的方法，记作IUGM(1,1) (Improved Unbiased GM(1,1))，目的是在提高原始数据光滑度，减小样本偏差的同时也提高样本对模型的适应性。其具体步骤如下：

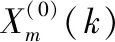
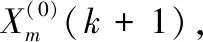
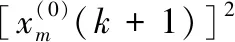
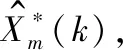
1.4 模型精度检验

模型精度反映模型预测的精确度，在初步选定模型后，要对各模型的精度进行检验，来判断其是否合理，经过检验合格的模型才可作预测。模型方法有：关联度检测、残差检测和后验误差检验模型(包括均方法检测和小误差概率检测)。对应的检测指标和相应的模拟精度等级见表1。

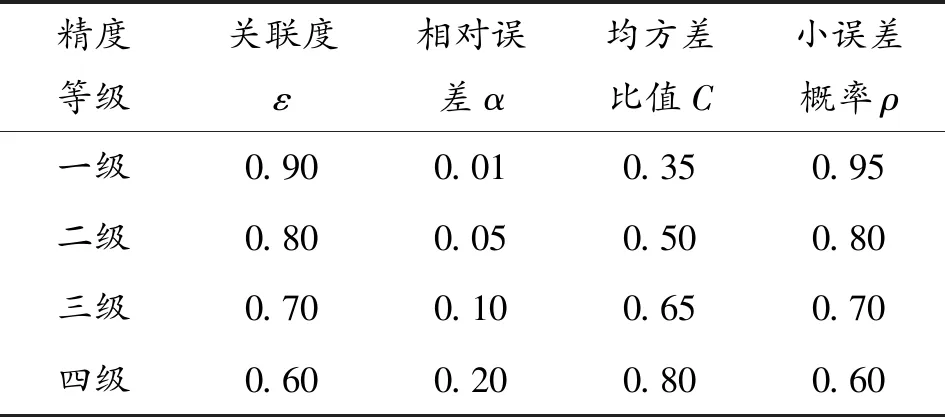
表1 精度检验等级表[13]

2 BP神经网络

2.1 传统BP神经网络模型

BP神经网络采用误差反向传播的方法来调整各层权值阈值，传统BP网络主要由一个输入层、一个或多个隐含层和一个输出层组成，隐含层中的神经元采用sigmoid型传递函数，输出层函数采用纯线性传递函数，其结构如图1所示。

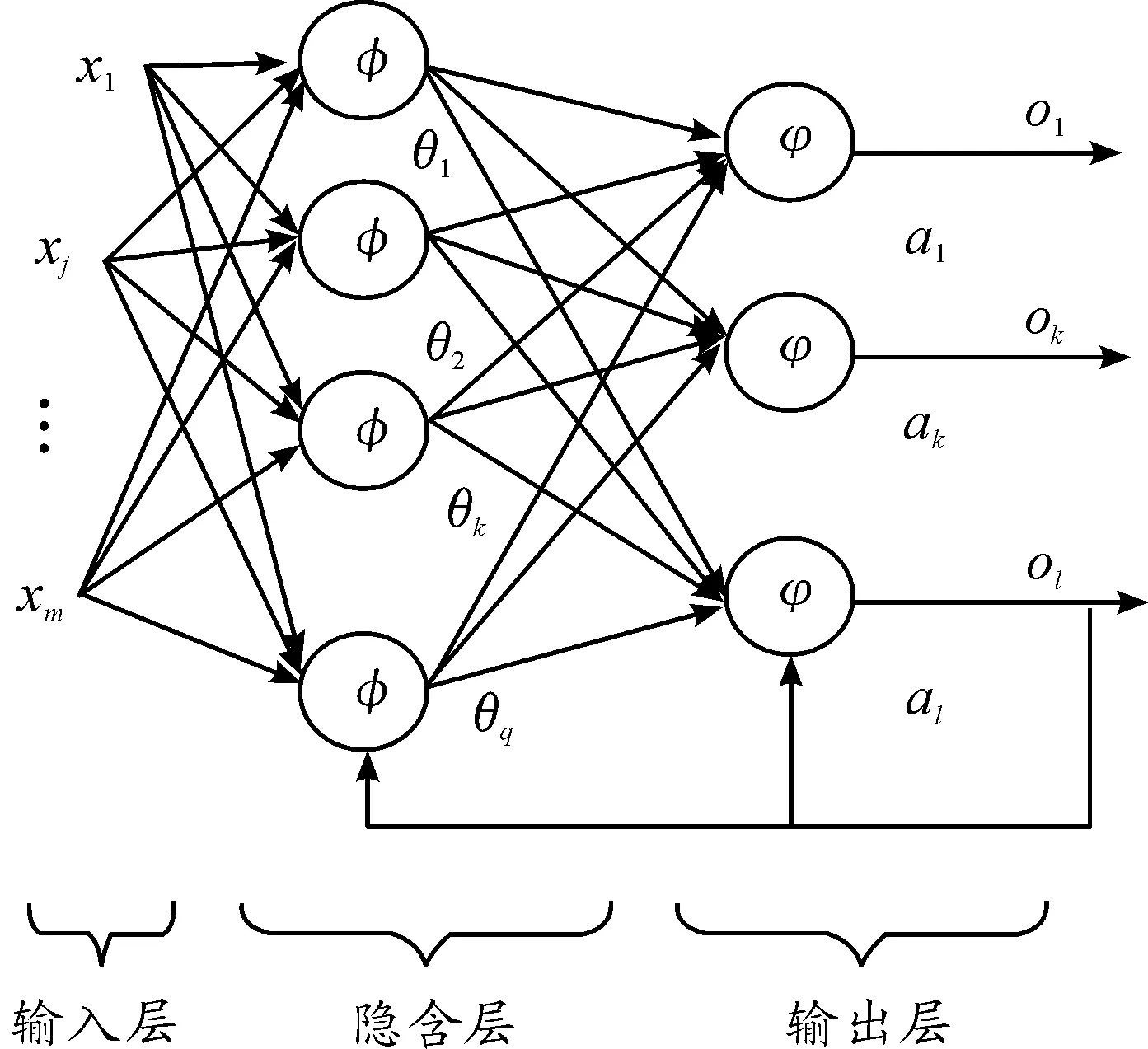
图1 BP神经网络结构示意图

其推导过程如下：

1) 输入信号正向传播过程。

隐含层第i个节点的输入为：

(10)

输出层函数为线性传递函数，则第k个节点的输入为：

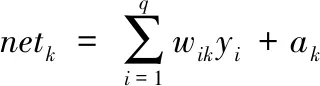
(11)

其中，yi=φ(neti)。

第k个节点的输出ok为：

(12)

定义误差函数：

(13)

式(13)中：Fk是第k个输出的真实值；Ek表示输出误差。预测值与真实值之间的误差越小，则说明预测精度越高。

2) 输入信号反向传播过程。

隐含层权值公式为：

wji=wji(t)+ηδjok+α[wji(t)-wji(t-1)]

(14)

输出层权值公式为：

wik=wik(t)+ηδiok+α[wik(t)-wik(t-1)]

(15)

式(15)中，η为学习率，η∈(0,1)；α为动量因子α∈(0，1)；t为调节次数；δ与偏差有关。

对于输出层：

δi=yi(1-yi)(Fi-yi)

(16)

对于隐含层：

(17)

2.2 BP神经网络的改进

改进后的BP神经网络(Improved BP neural network，IBP)结构中的动量因子与常规权值调整公式中常数项动量因子α0不同，改进后的动量因子是一个变量，其取值受前面输出误差的影响，且大小随输出误差比值大小做调整。按照经验可知，α0∈(0，1)，误差调整总体呈下降趋势。

现令：

α(t)=α0·E(t-1)/E(t)

(18)

则式(14)和式(15)可调整为：

wji=wji(t)+ηδjok+[α0·E(t-1)/E(t)]·

[wji(t)-wji(t-1)]

(19)

wik=wik(t)+ηδiok+[α0·E(t-1)/E(t)]·

[wik(t)-wik(t-1)]

(20)

同理可得阈值的调整公式，在此不作说明。

此外，学习速率η的取值对网络的训练性能也同样有一定影响，通常为一常数。η取值过小，会延长训练时间，训练收敛减慢；η取值过大，对网络稳定性降低起一定作用。综合考虑训练时间和稳定性两方面因素，参照预先设定的误差参数，提出对η取值进行调整，当网络输出误差较上一层输出超出设定值时，则减小η值，反之增加，直至网络训练收敛达到预期。η取值为：

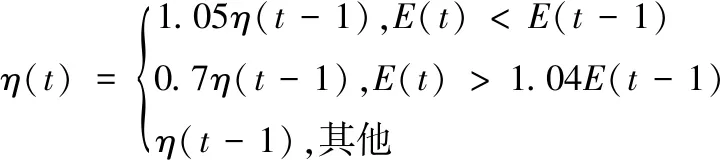
(21)

通过自动调整η来实现始终以最大允许速率对网络进行训练。

3 改进型灰色BP神经网络

3.1 灰色BP神经网络组合形式

灰色BP神经网络就是将灰色系统理论和BP神经网络结合在一起，对不确定问题进行求解的模型[14]。灰色理论模型与BP神经网络传统结合方式主要有以下几种[15]：

1) 串联型:将多个灰色预测模型预测的结果再通过BP神经网络系统进行预测；

2) 并联型：先采用灰色预测模型和BP神经网络系统分别进行预测，再对所有预测结果结合实际背景加权组合作为最终预测值；

3) 嵌入型：即在BP神经网络系统的输入层添加一个灰化层，在输出层添加一个白化层。

本文建立的改进型灰色BP神经网络(IUGM-IBP)模型采用串联式组合模型，即由改进无偏GM(1,1)模型和3层改进后BP神经网络串联而成。这是组合预测模型最常采用的连接方式，串联组合模型能够在不改变算法特性的同时兼具两种算法的优点。

3.2 改进型灰色BP神经网络组合预测算法步骤

改进型灰色BP神经网络预测结构如图2所示。改进型灰色BP神经网络组合预测算法步骤如下：

步骤1：将输入原始数据序列描述为X(0)=(x(0)(1),x(0)(2),…,x(0)(n))；

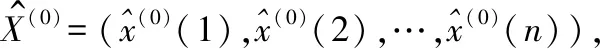
步骤3：对2个模型分别进行精度检验，如精度在允许范围内则可，如精度超出允许范围，则模型不可作预测；

4 实例应用

某型机载导弹导引头DSP控制器是导引头伺服控制系统的核心器件，其性能的好坏直接影响到系统的运算速度、精度和稳定性。对某型机载导弹导引头DSP控制器内部电压的大量实测数据按照时间进行分区处理，共分为12组实测区间数据，各区间数据经处理后其平均值分别是1.951 1、1.891 3、1.790 7、1.671 8、1.634 4、1.548 1、1.450 9、1.391 3、1.339 4、1.220 3、1.113 6、1.028 0。取前10个区间原始数据作为训练样本，经过GM(1,1)、UGM(1,1)和IUGM(1,1)建立模型，再将10个区间数据经处理后对应的残差作为期望输出样本。利用10个区间原始数据分别对传统BP神经网络和IBP神经网络进行训练，经训练后的组合预测模型对后2个区间平均数据进行预测。

4.1 几种灰色GM(1,1) 预测模型

4.1.1传统灰色GM(1,1)模型预测

将训练样本代入式(1)～(5)，可得到灰色GM(1,1)模型参数为：

[a,b]T=[0.025 8, 1.427 6]T

(22)

则由式(6)、(7)可得到灰色GM(1,1)模型预测值为：

(23)

4.1.2UGM(1,1)模型预测

将式(22)所得模型参数[a,b]T代入式(8)，可得到UGM(1,1)模型参数：

A=2.013 9,B=-0.056 3

(24)

则由式(9)可得到UGM(1,1)模型预测值为

(25)

4.1.3幂函数—新陈代谢法改进后的IUGM(1,1)预测模型

(26)

因此，可得到3种预测模型样本数据的拟合数值，见表2所示。

表2 不同模型拟合值

参照表1对上述预测模型进行精度检验，目的是判断3种模型的合理性，各项精度检验值见表3。

由表3可知，3种预测模型中传统灰色GM(1,1)和UGM(1,1)关联度超出允许范围，不适用于此类预测，IUGM(1,1)在4项指标上均符合精度检验，适用于此类预测。

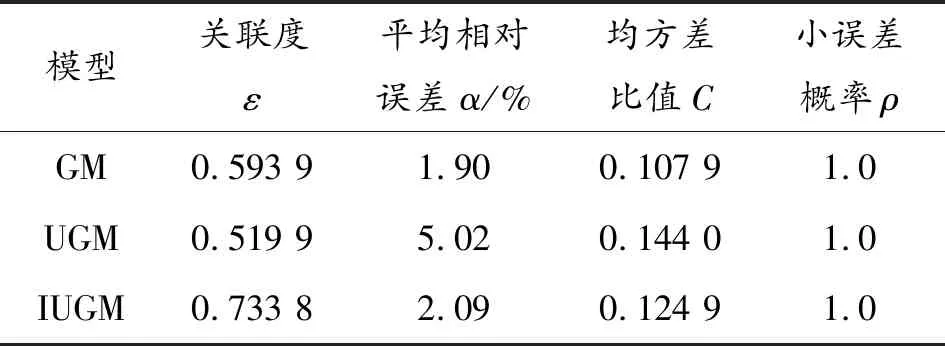
表3 不同模型各项精度检验值

4.2 灰色BP神经网络组合预测

将IUGM(1,1)预测模型对原始数据产生的拟合值每10个数据分成一组，作为BP神经网络训练的输入值，将下一数据拟合值与样本值的残差作为BP神经网络训练的输出值。BP神经网络隐含层节点按照经验公式选取15，则BP神经网络的结构为10×15×1。设网络训练次数为2 000次，训练目标0.000 1，w的初始取值在(-0.3,+0.3)内选取，η=0.05，θi(0)=0.9，ak(0)=0.9，隐含层中的神经元采用sigmoid型传递函数，输出层函数采用纯线性传递函数，对传统BP神经网络和改进后BP神经网络进行训练。

4.3 预测结果比较

利用IUGM(1,1)和传统BP神经网络、IBP神经网络组合预测模型对目标数据进行预测，共得到3组预测数据，各预测数据与真实值对应的相对误差见表4。

表4 3种预测模型预测数据

由表4可见，在每个数据区间中，灰色BP神经网络组合预测相对误差大大小于改进后无偏GM(1,1)预测。针对BP神经网络环节的改进，也使得综合预测效果更佳，预测值更接近实际值，对该部件性能预测更符合发展走向。说明改进后的灰色BP神经网络对某型机载导弹导引头DSP控制器的性能预测具有更好的适用性。

5 结论

对灰色GM(1,1)预测模型进行改进，分别利用传统灰色GM(1,1)、无偏灰色GM(1,1)和改进后的无偏灰色GM(1,1)结合实测数据对某型机载导弹雷达导引头DSP控制器内部电压参数进行预测。在传统BP神经网络基础上通过调整动量因子和学习速率的取值，对BP神经网络进行改进。将灰色GM(1,1)预测模型和改进前后的BP神经网络结合成新的预测模型，再对DSP控制器进行性能预测，预测结果表明，改进过后的组合预测模型预测精度更高，适用性更强。