内河航道测量波浪补偿装置设计及仿真分析
2020-07-04刘延涛
刘延涛
(连云港市航道管理处,江苏 连云港 222004)
0 引言
航道管理部门为了保障内河船只的运行安全,需要定期进行运河的维护,其中一项很重要的维护工作是内河河道水深数据测量。现有的水深测量方式采用GPS+测深仪安装在小渔船上进行工作,从而测得航道的水深数据[1]。但是测量时,当受到河面风、水流、过往船舶船行波等因素影响时,测量船会产生横摇、纵摇2个方向摆动及上下升沉,摆动使测量的声束不能垂直于河床。横摇、纵摇和升沉幅度越大,测量误差就越大,影响了水深测量的精度和效率[2]。
近年来,主动波浪补偿技术在船舶及海洋装备中逐渐使用,用来解决恶劣海况下,波浪引起的船体运动导致装备不能安全工作的问题,代表性的应用包括波浪补偿吊艇装置[3]、并联主动波浪补偿平台[4-5]等,但在内河航道测量船上还未有应用。
针对上述问题,本文设计了一种适合内河航道测量的波浪补偿装置,以实现对波浪运动引起的测量误差补偿,提高测量精度。
1 主要设计指标
本文根据内河航道测量船舶的船体大小和风浪数据,估算出船舶受波浪影响运动幅值,并通过实验分析出测量精度受船舶横摇、纵摇及升沉运动影响最大。其运动参数如下:
最大横摇幅值:±15°;最大纵摇幅值:±10°;最大升沉幅值:±200 mm;最大载荷:10 kg。
2 结构设计
根据上述补偿指标开展了补偿机构的方案设计和总体参数计算。本文设计波浪补偿装置能够实时有效地完成对波浪引起的横摇、纵摇、升沉进行补偿,同时在保证平台稳定运行的情况下,要尽可能做到质量小刚度大。通过分析对比各类串并联自由度平台的结构优缺点,结合河道测量工作环境情况,内河航道测量装置采用二自由度平台与升沉机构结合的串并联结构,其装置结构模型见图1。
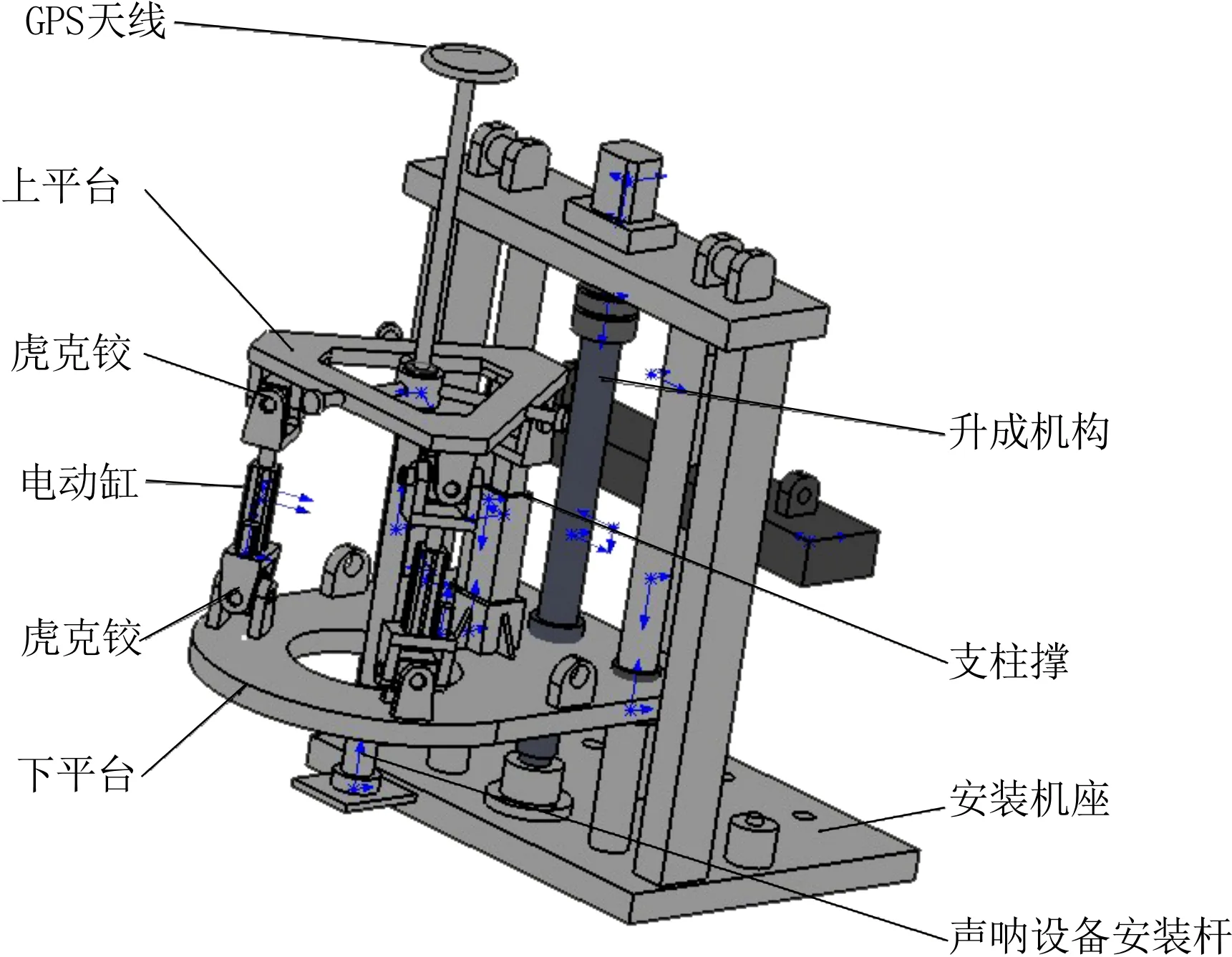
图1 内河航道波浪补偿装置
内河航道测量装置主要由升沉机构、上平台、下平台、安装基座、电动缸、支撑立柱、声呐设备安装杆、GPS天线组成。升沉机构的动力部件为伺服电机,固定在安装基座上端,传动部件为带有螺纹的丝杠。平台组件分为上平台与下平台。上平台与下平台之间通过2根电动缸和1个支撑立柱连接,且2根电动缸为伺服电动缸。电动缸与平台之间通过虎克铰相互连接。上平台装有安装杆,安装杆上连接有GPS天线与换能器。
串联机构也称升沉机构,采用直线电动缸,可以实现船舶在水上上下方向的运动补偿。并联机构采用2根电动缸并联形式,可以实现船舶在水上横摇纵摇的补偿;中间的支撑立柱保证了在串联机构对上下补偿后并联机构的再次补偿。本文将两机构联合起来,不仅结构简单,而且完全适用于内河航道的应用。
3 波浪补偿装置运动学模型
该波浪补偿装置是由串并联机构组成的混联机构。安装基座固结在船体上,随水上船舶模型做同步运动。升沉机构用于补偿船舶运动时的升沉运动,根据平台上安装的微惯导设备测量出来的上下运动位移数值,经处理之后,通过升沉机构中的丝杠调节,经下平台的上下移动实现对船体的升沉补偿。由于测量出来的升沉数值可以通过升沉机构方便快捷地实现相应的补偿,所以较为简单。
二自由度平台主要实现的是海浪中横摇纵摇对上平台影响的补偿。由于上下平台之间通过2根电动缸和支撑立柱相互连接,所以在分析运动状态时较为复杂,因此运动学方程对二自由度平台进行主要分析。
建立主动波浪补偿平台中二自由度平台的坐标系模型见图2。将下平台的坐标系设置为A0A1A2,上平台的坐标系设置为B0B1B2,中间支撑柱的矢量坐标为A0B0,其长度为L0并保持稳定不变,其余2根电动缸的矢量坐标分别表示为A1B1、A2B2。
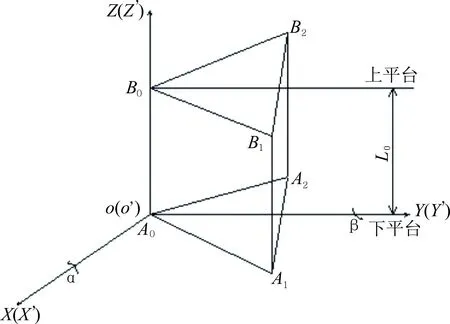
图2 二自由度并联平台的空间坐标系结构示意图
下部平台跟随船的侧倾、俯仰和升沉运动,而上部平台是补偿平台,理论上补偿后,该平台可以相对于地球坐标系保持相对静止。 根据笛卡尔坐标系原理建立静态坐标系和动态坐标系。 静态坐标系OXYZ的原点为A0,固定在上平台上。 动态坐标系O′X′Y′Z′的原点也是A0,固定在下部平台上。初始状态动坐标系与静坐标系保持一致,上平台与下平台之间的距离为L0,故下平台可以看成是随船体进行摇摆运动的平台,即绕X轴和Y轴作定轴旋转的平台。该波浪补偿平台中的二自由度平台可补偿船舶在水上的横摇纵摇运动。
根据图2的几何关系,可得出:
A为下平台在动坐标系中各铰接点坐标矩阵:
(1)
B为上平台在静坐标系中各铰接点坐标矩阵:
(2)
空间坐标变换如下:
(1)横摇变换,即动坐标系绕静坐标系的X轴转动横摇角α,变换矩阵为:
(3)
(2)纵摇变换,即动坐标系绕静坐标系的Y轴转动纵摇β,变换矩阵为:
(4)
(3)横摇纵摇的混合变换矩阵为:
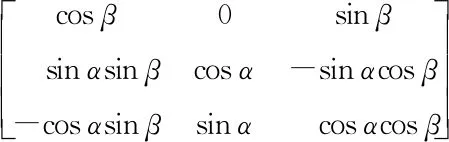
(5)
将下平台铰点转到静坐标系上,求得下平台铰点在静坐标系下的坐标矩阵为:
Q=RgB=[Qij]3×3
(6)
这样,由反解算式可得出LA1B1杆和LA2B2杆的伸缩量为静坐标系中上下平台铰点间距离减去电动缸原始长度:
(7)
式(1)~式(7)就是该波浪补偿平台横摇和纵摇补偿的反解算式。
4 波浪补偿装置运动学仿真
4.1 虚拟样机仿真模型
ADAMS是一个虚拟原型软件[6],可以实现3D建模和运动仿真。 用户可以方便地进行运动学分析和运动学机理的动态分析。 使用SolidWorks 3D软件对内河航道波浪补偿测量设备进行三维模型的建立,其中包括各个杆件的具体尺寸。由于SolidWorks中模型的细小部件的存在,会影响ADAMS的仿真,因此在导入到ADAMS之前,需要对三维模型进行简化分解。将简化后的模型导入到ADAMS软件中,设置好ADAMS仿真软件的仿真环境,对模型中各个相互连接的机构之间做好相关约束,其中包括转动副、移动副。为了方便观察仿真结果中上下平台的运动情况,以及各伸缩缸的伸缩情况,在SolidWorks中建立内河航道波浪补偿测量装置的装配体模型时,需要将安装基座的底座固定在 ADAMS 中的平行于全局坐标系XY的平面上,安装基座的底面需要与Z轴垂直。虚拟样机模型见图3。
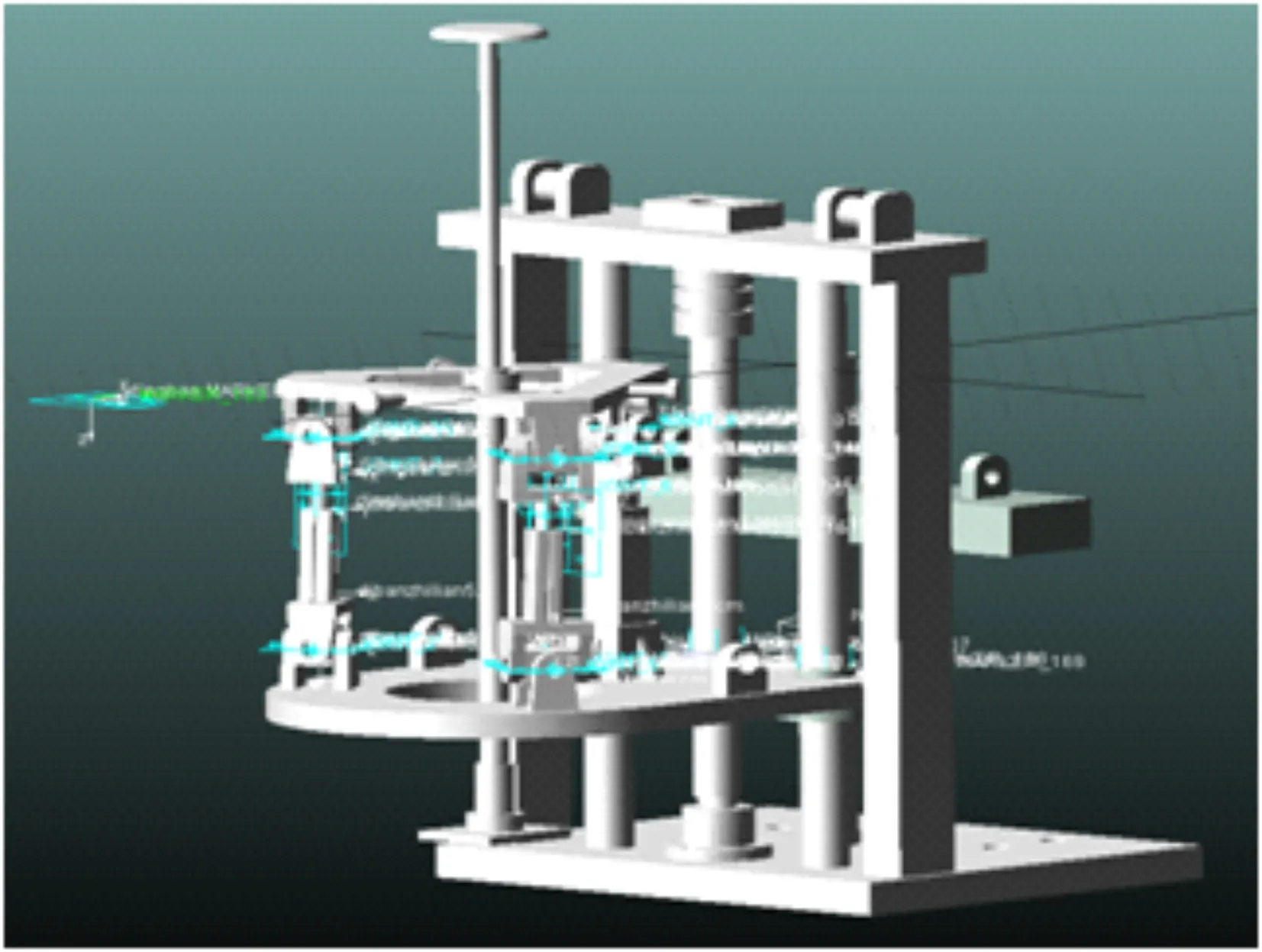
图3 波浪补偿装置约束设置
在进行波浪补偿装置模型运动学仿真之前,需要设置好ADAMS相关仿真环境参数。仿真环境设置如下:
(1)将仿真环境中各个机构的单位设置为国际单位MKS,便于在仿真结果中查看相关图形。
(2)由于进行运动学仿真,去除掉重力的影响,并且设置坐标系为笛卡尔坐标系,根据各机构之间的连接关系,设置相应的约束。
(3) 将波浪补偿装置置于平台上,在仿真环境中地面施加固定约束:升沉平台设置为移动副,上平台、下平台与电动缸之间设置成转动副,上平台与支撑立柱设置为转动副,下平台与支撑立柱设置成固定约束。将波浪补偿装置的机构约束设置好之后,在约束好的机构上添加模拟运动函数的驱动。
4.2 内河航道波浪补偿装置仿真分析
波浪补偿装置较复杂运动为二自由度机构,故对仿真模型分别施加横摇和纵摇2个驱动,仿真运动曲线设置为正弦函数。在电动缸末端的虎克铰设置1个测量标记点,在 ADAMS 仿真模型中该点命名为 kuai、kuai1,位于电动缸伸缩装置末端位置。在 ADAMS 中设置仿真参数为 5 s、500 步,对波浪补偿装置进行运动学仿真。仿真周期结束后,对标记shangpingtai、shensuogang、shensuogang 3进行测量,输出波浪补偿装置各个构件、杆件及末端测量点相关仿真结果。
将横摇的驱动函数设置成:
v=-0.05sin(10t)
式中:t为时间,s。
选取shensuogang、shensuogang 3为测量值,测量结果选取位移,得到在Z分量上的位移测量值,在 ADAMS 中处理绘制并得到其位移曲线,见图4。通过分析,发现波浪补偿装置仿真所得与实际运动情况相符合,从而验证了波浪补偿装置模型的合理性。
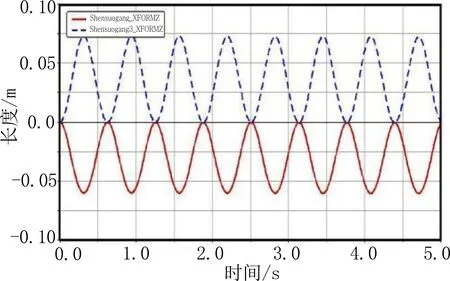
图4 横摇下电动缸位移曲线
由图中可知,横摇情况下,电动缸最大补偿长度约为0.072 9 m。由于在实际过程中电动缸在运动过程中并非竖直上下运动,其最大伸长值会稍大于0.05 m。
由于平台在海浪中随时会处于任意位置,故选取平台在非水平情况下放入水中。将纵摇的驱动函数设置成:
v=-0.02sin(10t)
选取shensuogang、shensuogang 3为测量值,测量结果选取位移,得到在Z分量上的位移测量值,在 ADAMS 中处理绘制并得到其位移曲线,见图5。
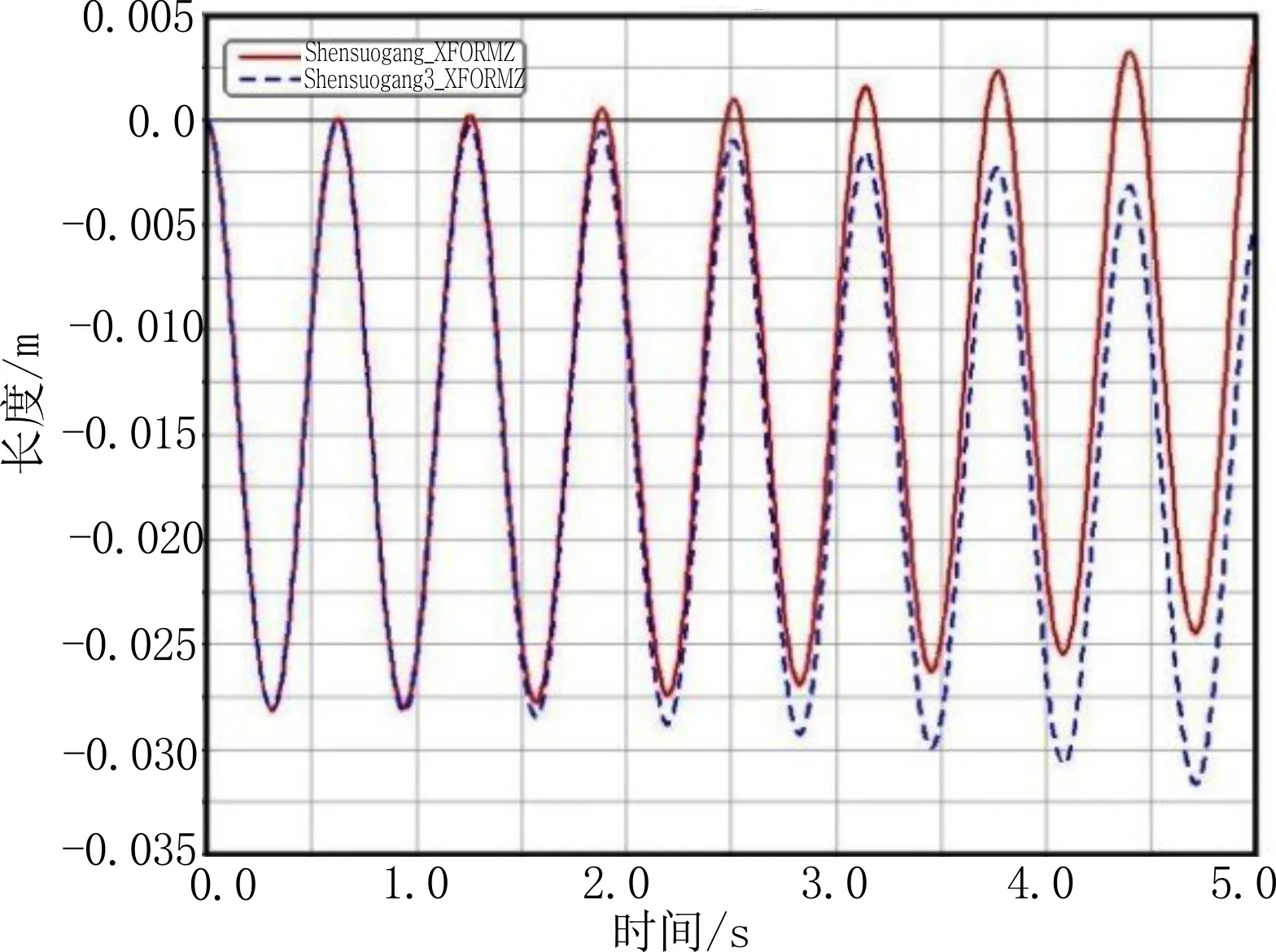
图5 纵摇下电动缸位移曲线
由图中可知,纵摇情况下,电动缸最大补偿长度约为0.028 8 m。由于初始shensuogang与shensuogang 3处于高低不等状态,导致铰链的直线距离不相等,伸缩长度会随着时间的变化产生偏移。
5 结语
针对水上波浪对船体摇晃的影响,提出采用串并联混合机构的波浪补偿装置,通过惯性测量装置测量位姿数据,由升沉机构补偿上下方向的波动,以及二自由度平台补偿波浪引起的横摇纵摇。对波浪补偿装置进行总体设计,并基于Solidworks软件建立波浪补偿装置三维模型,运用运动学反解算法计算电动缸杆长伸缩量,通过ADAMS软件对波浪补偿装置进行仿真,得到横摇纵摇情况下电动缸杆长的伸缩曲线,验证了设计的正确性,为下一步波浪补偿装置的制造奠定了基础。
