一种采用干扰观测器控制的交流伺服调速系统设计

郑丽楠，陈世明

（1.吉林铁道职业技术学院城市轨道交通学院，吉林吉林132000；2.华东交通大学电气与电子工程学院，江西南昌330000）

受益于工业革命的影响，全球工业得到了快速发展，随着工业制造4.0以及智能制造等技术的出现，交流伺服系统也渐渐被人们用于替代直流伺服系统。由于交流伺服系统具有效率高、结构较简单以及易控制等优点，其被广泛应用于工业机器人技术、数控技术以及航空航天技术等领域[1]。近些年，电子科学技术的不断发展为交流伺服系统的调速提供了坚实的技术支持，通过交流伺服调速控制系统，人们可以对交流伺服的转速进行控制，从而使得交流伺服系统变得更加灵活，更加精准[2]。

在交流伺服系统中，输出转速的控制尤为重要，对输出转速的精确、平稳控制有助于提高交流伺服系统的应用范围及其工作性能。当下出现了较多的伺服调速系统，例如：Ohishi等[3]提出了一种矢量控制异步电动机电压饱和的高性能伺服调速系统，该系统允许比例积分控制器输出的电压饱和，以使得矢量控制条件下的相位误差得到快速修正，使矢量控制条件得以保持，实现对输出转速的控制。除此之外，Preindl等[4]还将预测控制方法引入到伺服调速系统的控制中，通过构造有限控制集模型，并利用该预测控制方法获取电压控制量，以实现对电机转速调控的效果。De Santana等[5]采用状态空间法对转子磁链定向的磁链进行建模，通过优化目标函数，考虑控制力和预测输出（速度和转速）之间的差异，推导出控制方法，利用扩展卡尔曼滤波器估计转子磁链和速度，实现转速的控制。Errouissi等[6]针对网络策略控制方法不能完全消除参数失配和外部扰动情况下的稳态误差，在考虑输入约束的条件下，设计了一种扰动观测器，用其实现对不同负载转矩产生的转速量差异进行评估，并通过级联比例积分实现对转速的控制。以上方法虽然都能够对伺服调速系统的输出转速进行控制，但由于这些方法存在解耦不完全以及参数难确定等问题，导致对输出转速的控制过程波动较大，而且准确度不高。

对此，本文采用干扰观测器设计了伺服调速控制系统，建立伺服调速设备控制器的结构模型，利用P控制器对可测干扰进行补偿，通过积分绝对误差（IAE）对设备输出的瞬时速度进行度量，以分析控制回路处于稳态的条件。采用滤波器和控制器对输入干扰进行补偿，通过设备的传递函数获取控制器的控制参数，抑制超调量。将控制器的零极点形式与二阶低通滤波器相结合，形成干扰观测器，并以P控制器为基础，设计了滤波PI干扰反馈控制器，以对输出转速进行控制。实验结果显示，所提方法不仅能够对输出转速进行准确的控制，而且控制过程波动较小，平稳度较高。

1 伺服调速设备的控制过程分析

对于具有输入干扰di的伺服调速设备，其控制器结构为

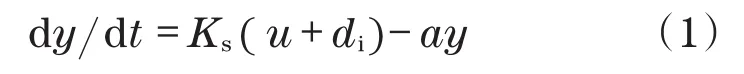
式中：u，y分别为设备的输入信号和输出信号；a为调节系数，Ks为设备的弹性系数。

将式（1）转换成零极点形式为

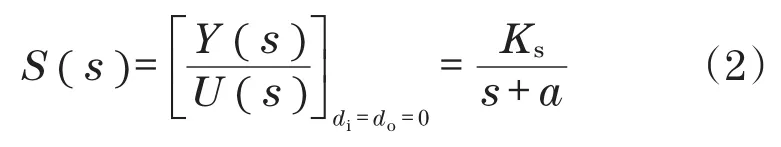
式中：Y（s），U（s）为输入信号和输出信号在s时刻的值。

通过P控制器对可测干扰进行补偿，可得[7]

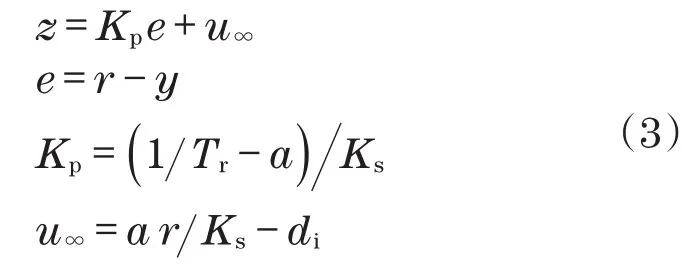
式中：z为状态控制器；e为新设定点参考值与y的误差；Kp为P控制器的增益；r为新设定点参考值；u∞为静态前馈控制量。

通过式（3）可见，u∞对应于静态前馈控制，使y∞=r保持稳定状态。当时间常数Tr＞0（闭环极点α=-1Tr＜0）时，式（2）所示的闭环设备为稳态。这种极点配置控制目标可定义为“使输出y从初始值y0在最短时间常数Tr内变为新设定点参考值r”。然而，这并没有提供关于最优控制器调整的信息。由于通常不对输出和扰动量进行测量，同时，由于设备参数未知，输出测量受到测量噪声和非模型动力学的影响，因此，控制问题还未能得以解决。

线性一阶设备从稳态y0到新的稳态y∞输出时的单调瞬变y(t)，对应两个单调区间组成的单脉冲输入u(t)。对于稳定设备（a＞0），可通过单调输入实现单调输出响应。

对于单积分器，通过输出求导可以找到与所需的S形单调输出相对应的单脉冲输入。当需要一个相对快速的闭环动力学时，单脉冲对于所有一阶装置来说都是典型的控制对象。干扰阶跃响应yd(t)会使设备的输出出现偏差，而控制器在修正该偏差时，需要一定的耗时。对于单个积分器，通过对输出进行求导，便可找到与所需的S形单调输出相对应的单脉冲输入。因此，设备的输出偏差大小与单脉冲输入的形状相对应。

在此，将利用归一化总方差对所需单脉冲输入的偏差T进行度量[8]，得

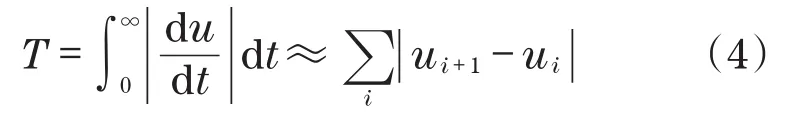
式中：T为所需单脉冲输入的偏差值。

对式（4）叠加振荡影响um=max(u)后，可变形为

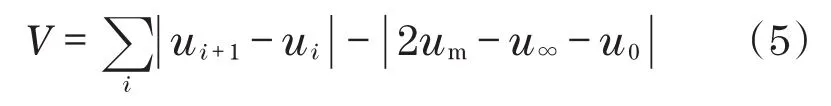
式中：ui为i时刻的输入信号；u0为i时刻的输出信号；um为i时刻的叠加干扰影响信号。

设备输出的瞬时速度I为

利用二阶低通滤波Qn(s)对式（2）进行滤波，可得

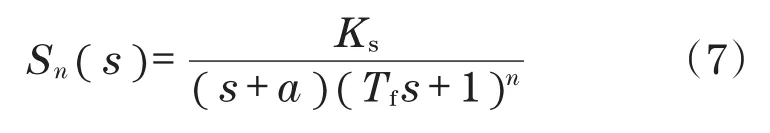
其中，

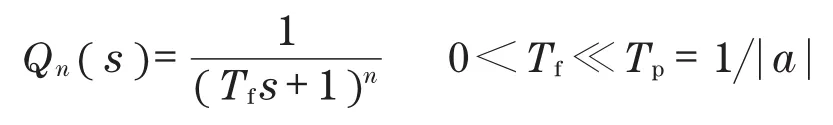
式中：Tf为加权系数。

尽管Sn(s)具有完全可控性和可观测性，但基于状态观测值u=fr+r'x，r∈Rn+1，状态向量x∈Rn+1，将极点配置控制扩展到滤波反馈值Sn(s)中，并不能够适应所有的回路状态[9]。因此，对于满足条件0＜Tf≪Tp=1|a|的Qn(s)参数，保留主要设备动力学导出的P控制器（见式（3）），并通过限制α=-1Tr的选择来考虑额外的动力学仍然是有必要的。

从所有可能的回路输入到输出的传递函数都具有特征多项式An(s)[10]：

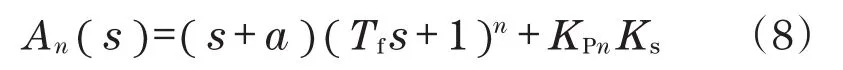
式中，KPn为P控制器n时刻的增益。

从根轨迹分析可见，带P控制器回路的最快非振荡瞬变对应于满足条件A(s0)=0和[dAds]s=s0=(s0)=0的An(s)的双实主极s0。对此，KPn和s0n可表述为

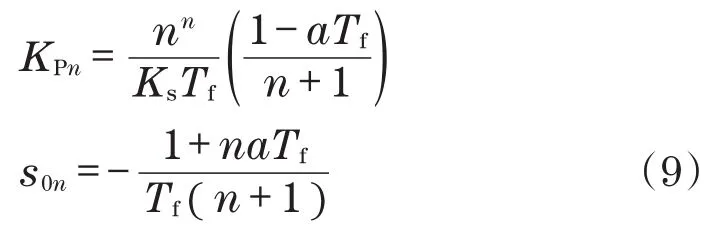
通过式（9）可见，当状态因子s0n＜0时，控制回路处于稳定状态。

2 控制系统设计

2.1 输入干扰补偿

在一个自由度的速度值C(s)设定点步骤之后，在积分和不稳定过程中，通常会出现输出超调的情况，此时可通过抑制参数Fp(s)扩展C(s)来抑制超调部分的影响。

抑制参数Fp(s)及C(s)的表述为

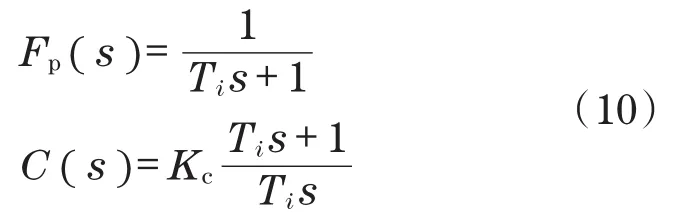
式中：Ti和Kc为控制参数。

通过Fp(s)及C(s)求取式（2）的传递函数的双实极为

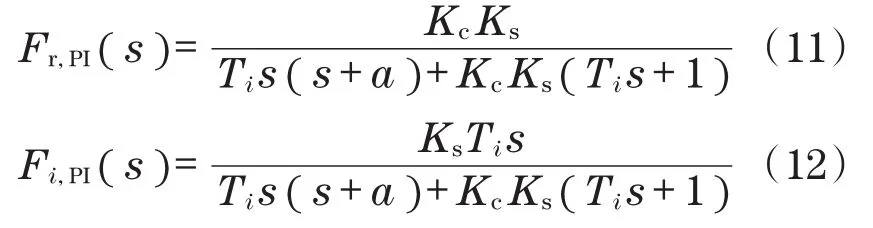
当公式

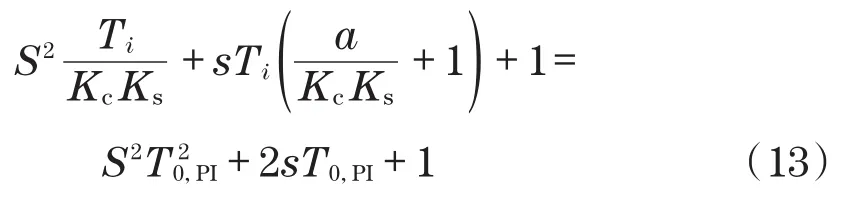
成立时，式（2）的传递函数存在双实极，T0，PI为P控制器的初始值，Fr，PI(s)和Fi，PI(s)为式（2）传递函数的双实极。

设定点和干扰量的补偿值Ir，PI和Ii，PI为

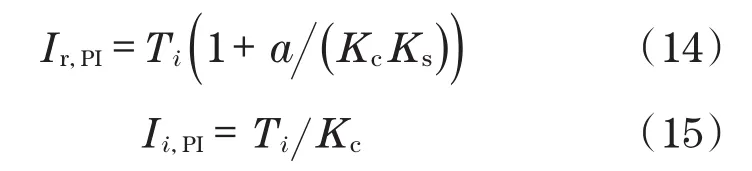
联合式（13）和式（15），可求取控制器参数Kc及Ti：

2.2 DO-FPI滤波反馈控制器设计

本文在P控制器的基础上设计了一种如图1所示的DO-FPI控制器。该DO-FPI控制器不需要任何并行积分操作，而且Qn也包含在P控制器的主反馈中。由此可见，最佳增益Kp=Kpn的值可随着变量n自适应的变化，与di对应的传递函数Fin(s)为

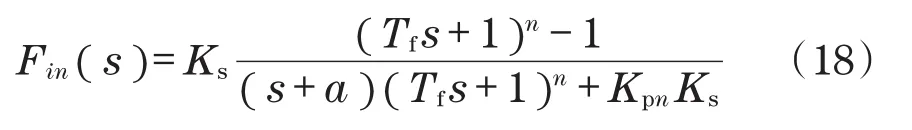
从式（18）可见，从Fin(s)=0开始，常数扰动不会引起任何永久误差。

与基于开环分析的方法不同，DO-FPI控制器不需要对滤波器结构及其时间常数进行特定限制[11]，因此，通过式（9）的增益可求取Iin：

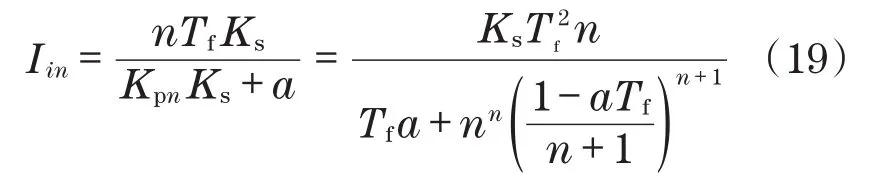
当a=0，且为Iin的期望值时，通过式（19）可求取Tf：

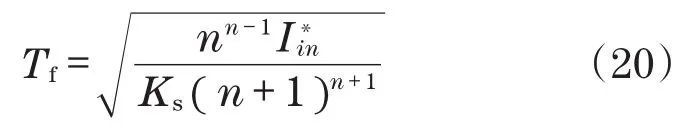
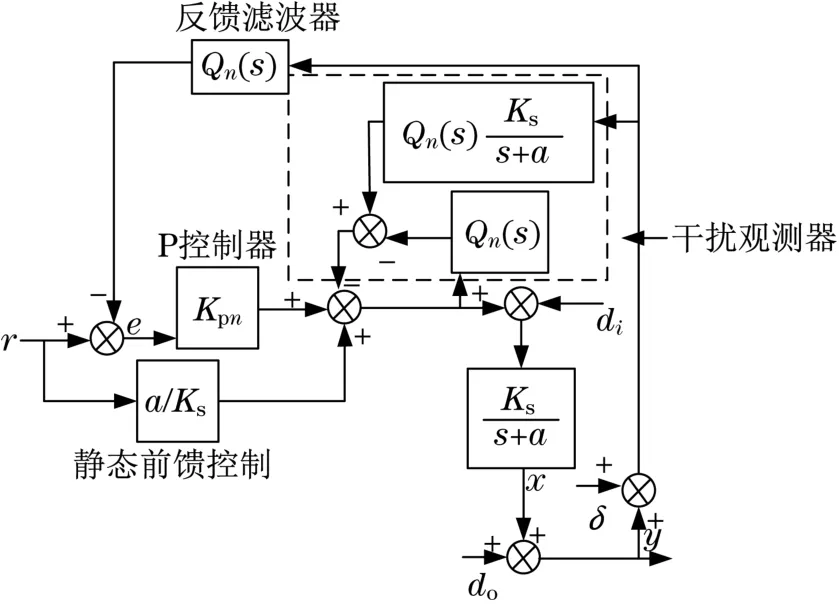
图1 DO-FPI滤波反馈控制器结构图Fig.1 Structure diagram of DO-FPI filter feedback controller

3 实验结果与分析

为了验证所提方法的有效性，利用Matlab/Simulink软件对所提方法的控制性能进行仿真。实验中所用感应电机的参数如表1所示。实验中摩擦系数B=0.005N·m·s·rad-1，滤波器阶数n=2，Ii的预期值。

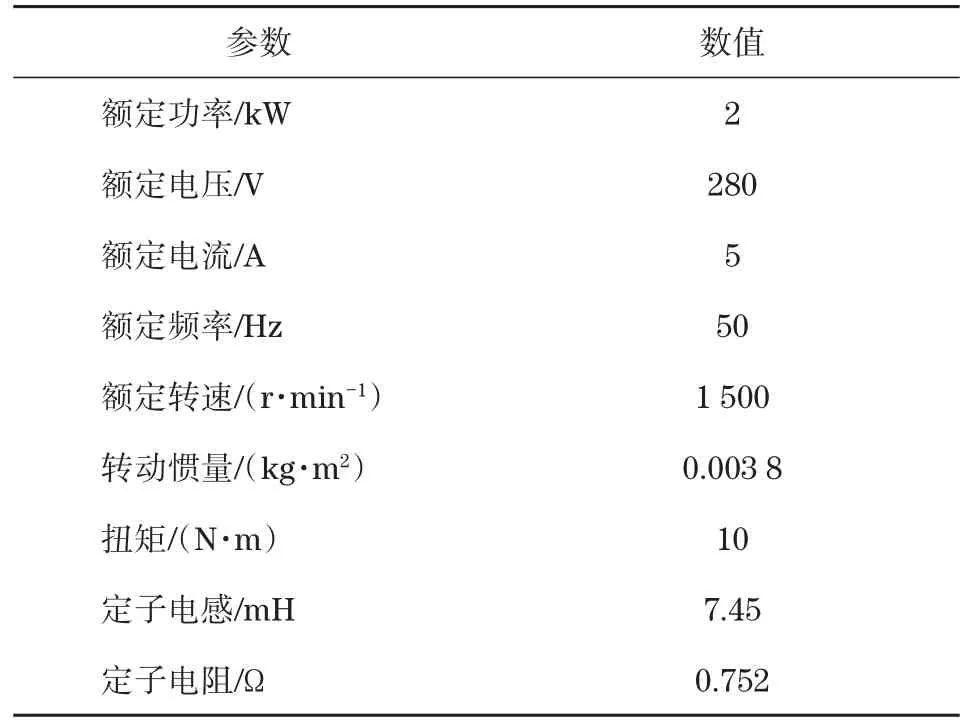
表1 感应电机参数Tab.1 Parameters of induction motor

实验采用曲线跟踪的方法，即设定一个目标输出曲线，然后利用所提方法对目标输出量进行跟踪，根据跟踪输出曲线对所提方法的控制性能进行分析。

所提方法与PI控制器对目标输出曲线的跟踪结果如图2～图5所示。由图2为所提方法与PI控制器对阶跃目标输出曲线的跟踪结果。从图2可见：两种方法对阶跃目标输出曲线的跟踪效果都较好。但将两种方法的跟踪输出曲线进行对比可见，PI控制器的跟踪输出曲线比所提方法的跟踪输出曲线更为陡峭，而且更晚趋于目标输出曲线。图3为所提方法与PI控制器对正弦目标输出曲线的跟踪结果。通过对比图3中两种方法的跟踪输出曲线发现，PI控制器的跟踪输出曲线较所提方法的跟踪输出曲线，具有更大的超调量。不同方法对方波目标输出曲线的跟踪结果如图4所示。由图4可见：所提方法的跟踪输出曲线比PI控制器的跟踪输出曲线更为平滑，而且超调量更小。图5为不同方法对不规则目标输出曲线的跟踪结果。由图5可知：PI控制器的跟踪输出曲线比所提方法的跟踪输出曲线，具有更少的波动次数，而且在目标输出曲线的变化处波动幅度更小，当出现超调时，所提方法能够更快地对跟踪输出曲线进行调整，使之能够更快地趋于目标输出曲线。说明所提方法在对伺服调速系统的输出转速控制过程中更为精准，更为快速，产生的波动也较小，能够更好地对伺服调速系统的输出转速进行控制。

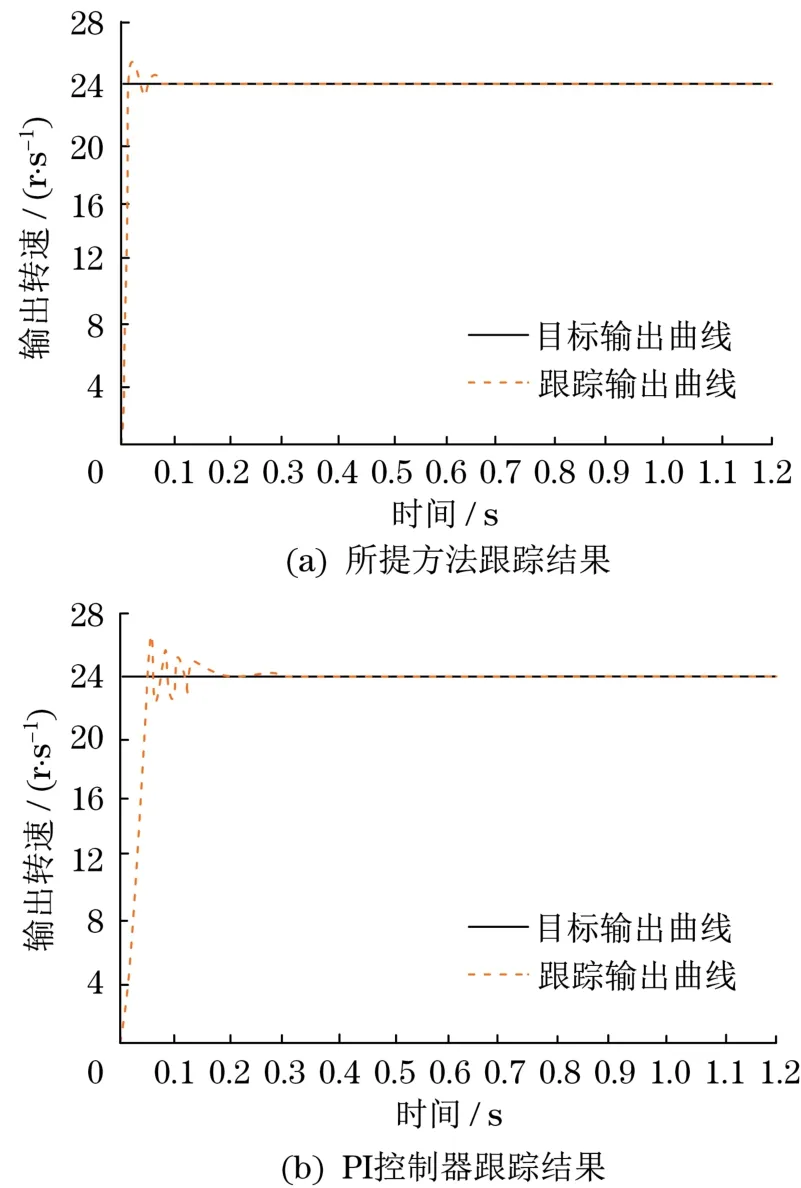
图2 阶跃信号跟踪结果Fig.2 Step signal tracking results

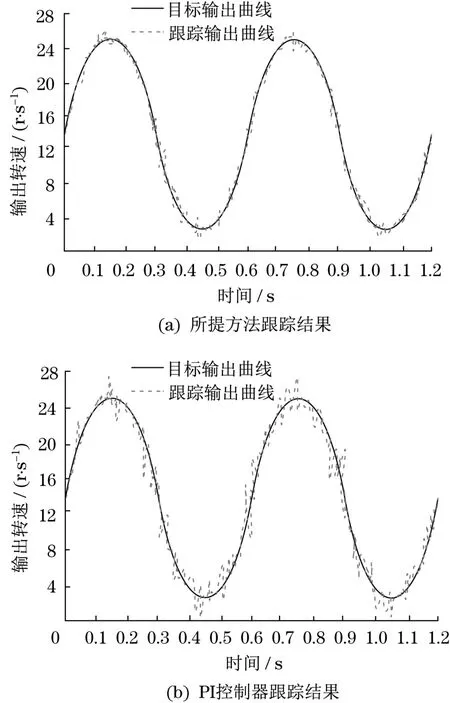
图3 正弦信号跟踪结果Fig.3 Sinusoidal signal tracking results

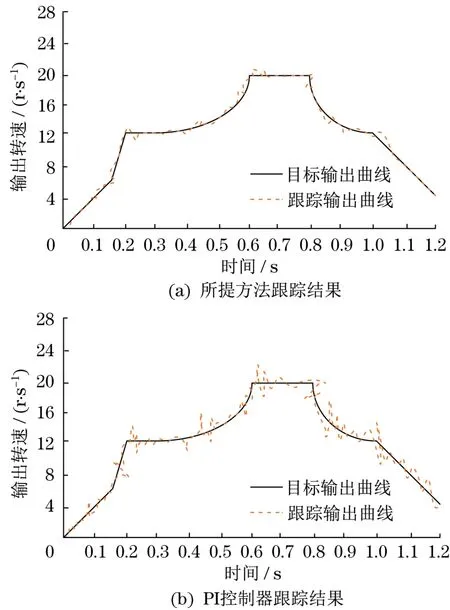
图5 不规则信号跟踪结果Fig.5 Irregular signal tracking results

4 结语

本文提出了一种采用干扰观测器控制的交流伺服调速系统设计的研究。通过伺服调速设备控制器的结构模型，求取其对应的零极点形式。利用P控制器分析控制回路处于稳态的条件，通过滤波器和控制器对输入干扰进行补偿，以对超调量进行调节。在P控制器的基础上，利用二阶低通滤波器构造干扰观测器，形成DO-FPI滤波反馈控制器，实现对输出转速的准确调控。通过对不同激励信号产生的目标输出曲线进行跟踪可见，所提方法能够较为平稳、快速和准确地对输出转速进行调控。