基于MATLAB的人字架优化设计

黄立言* 王彦伟

（武汉工程大学 机电工程学院）

1 MATLAB优化工具箱简介

MATLAB 是由美国MathWorks 公司发布的主要面向科学计算、数据可视化及数值计算的高级技术计算语言和交互式环境，简称矩阵实验室[1]。MATLAB是一个集强大的科学计算、完美的可视化功能、完善的自我帮助系统的开放式交互的大型软件，现已广泛应用于数学物理、材料化工、机电自动化、管理金融、生物医药、海洋科学、航天军工、语音处理以及社会科学等各个领域，种类繁多且不断拓展的工具箱使MATLAB 软件深受科研工作者的青睐。MATLAB 优化工具箱（optimization toolbox）是基于MATLAB 的面向最优化求解的专用工具箱[2]，其主界面如图1 所示。MATLAB 优化工具箱几乎可以完美求解各类优化问题。其高效简洁的函数表达和对算法参数的自由设置便于用户调用各类优化函数，利用MATLAB 优化工具箱可以求解线性规划、非线性规划和多目标规划问题。此外，该优化工具箱还提供了线性、非线性最小化、方程求解、曲线拟合、最大最小问题和半无限问题等的求解方法，为优化方法在实际工程应用中提供了更加有效、方便、快捷的途径。现将MATLAB 优化工具箱中常用优化函数进行了归纳，如表1 所示。

图1 MATLAB优化工具箱主界面

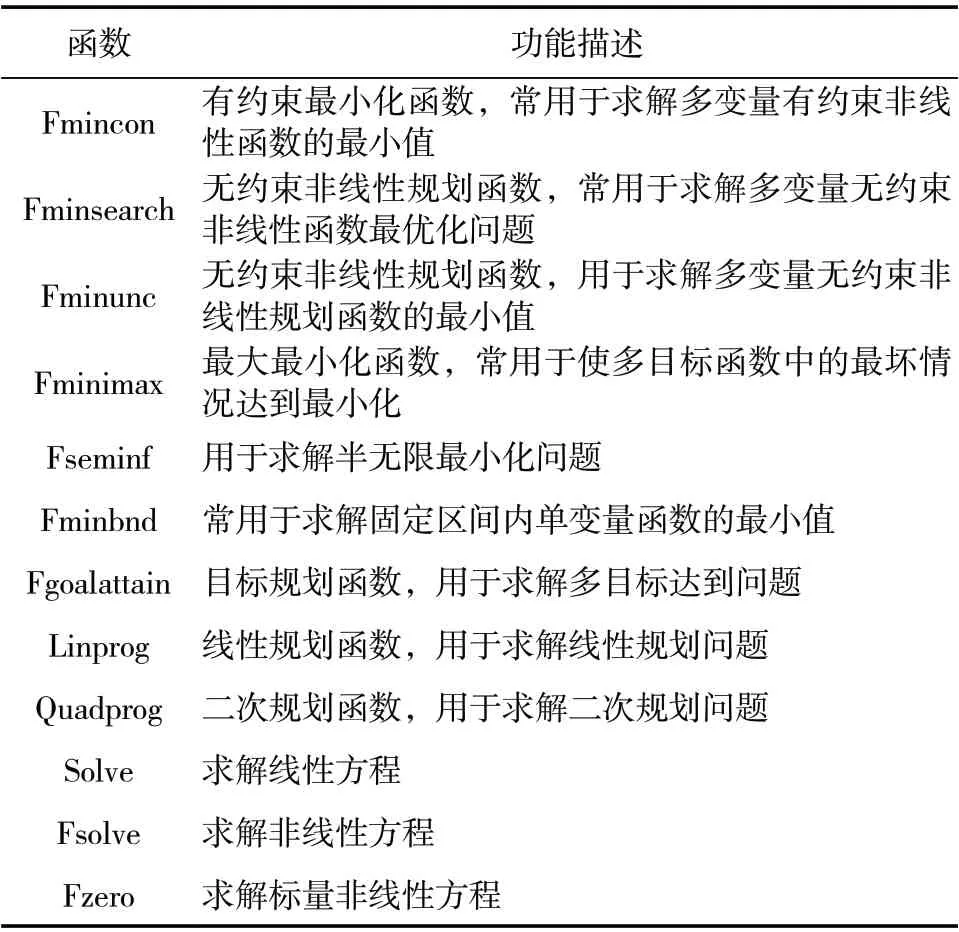
表1 MATLAB优化工具箱常用优化函数

2 优化问题示例

人字架应用十分广泛，其主要由2 根钢管构成，如图2 所示，其顶点受到的外力为2F = 3× 105N。已知人字架跨度2B = 152 cm，钢管壁厚I = 0.25 cm，钢材弹性模量E = 2.1× 105MPa，材料密度 ρ = 7.8× 103kg/m3，许用压应力[σy]= 420 MPa。要求在钢管压应力σ 不超过许用压应力[σy]和失稳临界应力σe的条件下，选取合适的人字架高度h 和钢管平均直径D，使钢管总质量m 最小[3]。

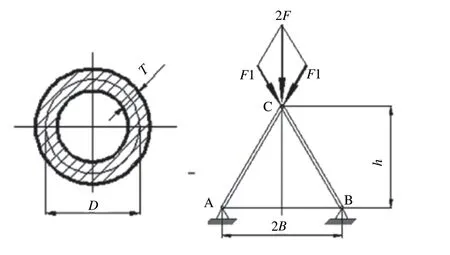
图2 人字架受力简图

2.1 确定设计变量

将人字架的高度h 和钢管平均直径D 作为优化设计变量（上标T 表示转置）：

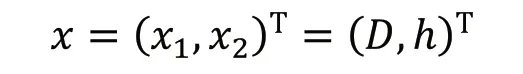
设计变量初始数据如表2 所示。

表2 初始数据表

2.2 确定目标函数

根据前文所述简化模型，可建立如下目标函数：

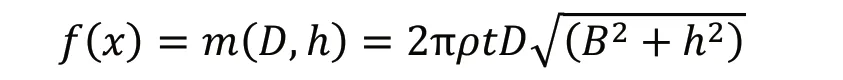
2.3 确定约束条件

强度约束条件σ ≤[σy]，即钢管所受的压应力 不超过许用压应力[σy]：

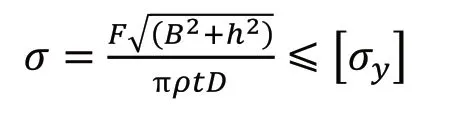
稳定性约束条件σ ≤σe，即钢管所受的压应力σ 不超过钢管的临界压应力σe：

根据设计经验，边界约束条件可设置为：

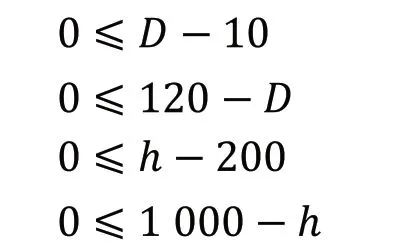
2.4 优化数学模型

综上所述，将所有函数规格化，则人字架优化设计的数学模型可表示为：

3 优化

3.1 优化步骤

根据之前建立的人字架优化模型及相关参数，利用MATLAB 优化工具箱对人字架进行优化设计。这是一个多维有约束非线性问题，其优化流程可简要概括如下：

（1）编写目标函数的M 文件；

（2）编写描述非线性约束的M 文件；

（3）设置相关参数，选择合适的优化方法，调用MATLAB 优化工具箱进行优化；

（4）得出结果，并进行分析。

3.2 优化结果

根据优化后的数学模型，利用MATLAB 优化工具箱进行求解。代入已知数据后，经34 次迭代，计算收敛，求得最优解。徐发滨[4]以人工神经网络为基础，介绍了一种基于遗传算法的反馈Hopfied 神经网络算法，并构造了工程结构优化模型；郭惠昕等[5]针对非线性约束问题，提出了一种新的、可行的混沌最优化算法——三次载波混沌最优化算法，并将该方法应用于工程结构优化设计；李文勇等[6]针对优化问题中的多极值现象，提出了一种基于有记忆模拟退火的全局优化算法，并针对不同的设计变量采用了不同的邻域产生方法。为了验证本文方法的可靠性，分别根据徐发滨[4]、郭惠昕等[5]、李文勇等[6]提出的方法进行了详细计算，并对结果进行了比较，如表3 所示。

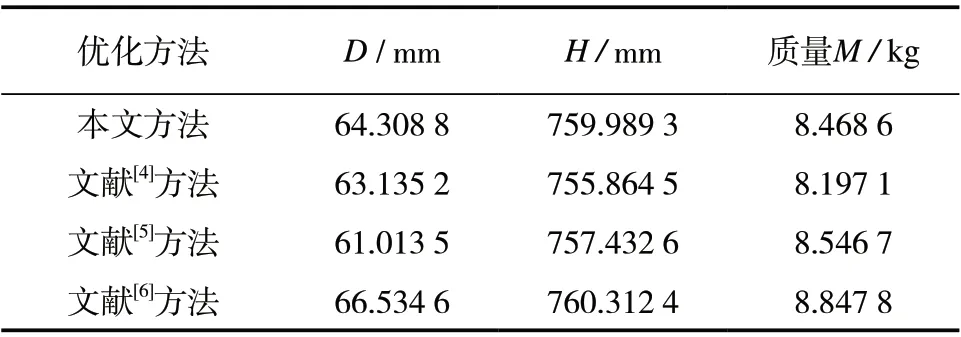
表3 不同优化方法计算结果的比较

由表3 可知，本文的计算结果与文献[4-6]中的方法计算结果接近，表明本文介绍的方法有较强的可靠性，可以应用于实际工程问题。

4 结论

通过人字架的优化实例可以看出，MATLAB 应用十分广泛，也是进行科研设计工作的利器，是解决机械优化设计的重要工具。利用MATLAB 优化工具箱中已有的优化求解函数，能够方便快捷地对最优化问题进行求解，避免了繁琐的算法设计和程序编写，节约了大量精力和时间，大大提高了设计者的工作效率，有较强的使用价值。MATLAB 优化工具箱求解方便快捷，精度高，速度快，结果稳定可靠，且程序简明，能很好地实现优化设计的算法过程。