基于修正θ投影法的GH4169高温合金蠕变寿命预测
2020-07-03李荣华张国铭
张 爽,刘 峰,李荣华,张国铭
(辽宁石油化工大学机械工程学院,辽宁抚顺113001)
我国石油、动力、航空航天等领域的相关技术随着工业技术的进步而发展迅速,设备工业环境温度也越来越高。设备长期在这样的环境中服役会发生蠕变现象,缩短设备的使用寿命。在长时间服役的过程中,蠕变破坏成为制约构件完整性的一个重要因素[1-2]。因此,蠕变寿命的预测与研究对高温设备的设计显得极为重要。但是,在实际工作环境中,通常高温设备的蠕变寿命较长[3-4],一般为几年甚至十几年,很难直接通过长时间实验来获取蠕变数据[5],因此国内外的许多学者研究了可在短时间内预测材料在实际工作环境中蠕变寿命的方法。例如,θ投影法[6]、Omega法[7]、G-W 法[8]和蠕变损伤力学方法[9]等。其中,θ投影法是20世纪80年代由英国的R.W.Evans等[6]提出的,该方法被推出后得到了学者的广泛认可。R.W.Evans等[10]利用此方法研究了电厂设备的使用寿命,并且对设备寿命的预测进行了大量研究;Molf用该方法对316L不锈钢在服役条件下蠕变参数进行了预测[11];Kim利用此方法对哈氏合金的蠕变性能进行了研究[12-13]。通常蠕变实验是基于恒载荷条件下所做的实验,与基于恒应力的结果有所差异,因此对θ投影法进行了修正,使之适用于恒载荷的条件,因此被称为修正θ投影法[14]。本文通过修正的θ投影法对GH4169的蠕变寿命曲线进行预测,进而对该种材料的蠕变寿命进行了估算。
1 实验部分
1.1 实验材料
实验材料是抚顺特殊钢股份有限公司的GH4169合金棒,材料的化学成分见表1。
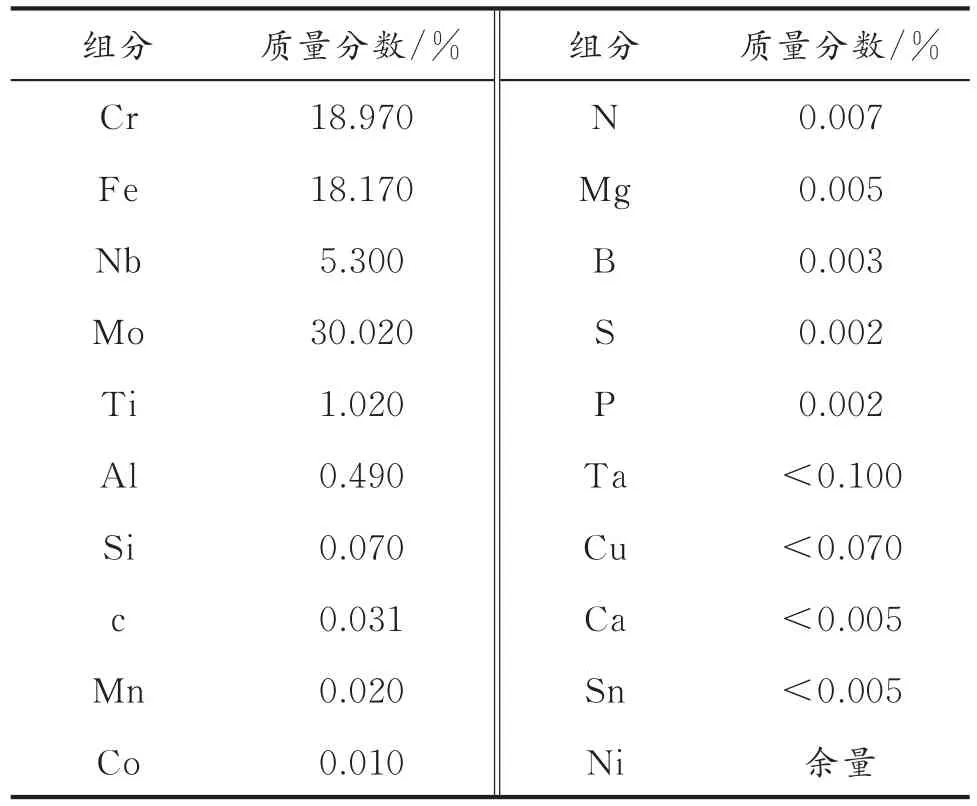
表1 GH4169合金棒的化学成分
1.2 实验方法
进行高温蠕变实验时,为了确保试样表面及形状精度不受损坏,通过线切割的方法将GH4169合金棒加工成矩形试样,其总长L为40.0 mm,标距L0为28.5 mm,具体尺寸如图1所示。试样加工参照GB/T 2039—2012《金属材料单轴拉伸蠕变实验方法》。对加工好的高温蠕变试样工作部分和过渡段进行机械抛光至表面没有明显划痕,然后挂置在高温持久实验机上,进行预加载、加热、保温、实验,保温时间为1 h;对试样进行高温蠕变拉伸实验,直至试样断裂,或保载600 h停止实验;待加热炉内温度小于60℃时取出试样,置于干燥器内待用。针对温度、应力两种不同的参数分别进行高温蠕变拉伸实验。实验条件:温度为660 ℃,应力为700、740、760、790 MPa;温度为650 ℃,应力为770、790、810 MPa。在不同的条件下进行蠕变实验,并绘制蠕变寿命曲线。
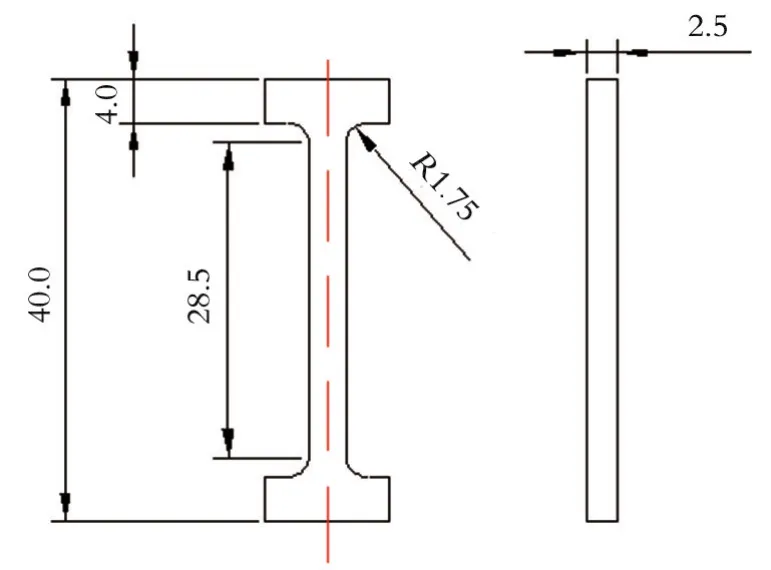
图1 蠕变实验试样(单位:mm)
2 结果与讨论
2.1 实验结果
在恒载荷,温度为660 ℃,应力为700、740、760、790 MPa及温度为650℃,应力为770、790、810 MPa的条件下进行高温蠕变实验。GH4169高温合金的蠕变实验数据和拟合曲线如图2所示。从图2可以看出,蠕变的三个阶段并没有全部显现出来,只有第二、三阶段比较明显,而且蠕变第二个阶段占整个蠕变曲线中所占比重较多;应力、温度与断裂时间呈相关性;在相同的温度下,蠕变断裂随着应力的变化而变化;在应力相同的条件下,随着温度的升高,断裂时间逐渐减小。由此可以得出,蠕变寿命与温度及应力都存在相关性。
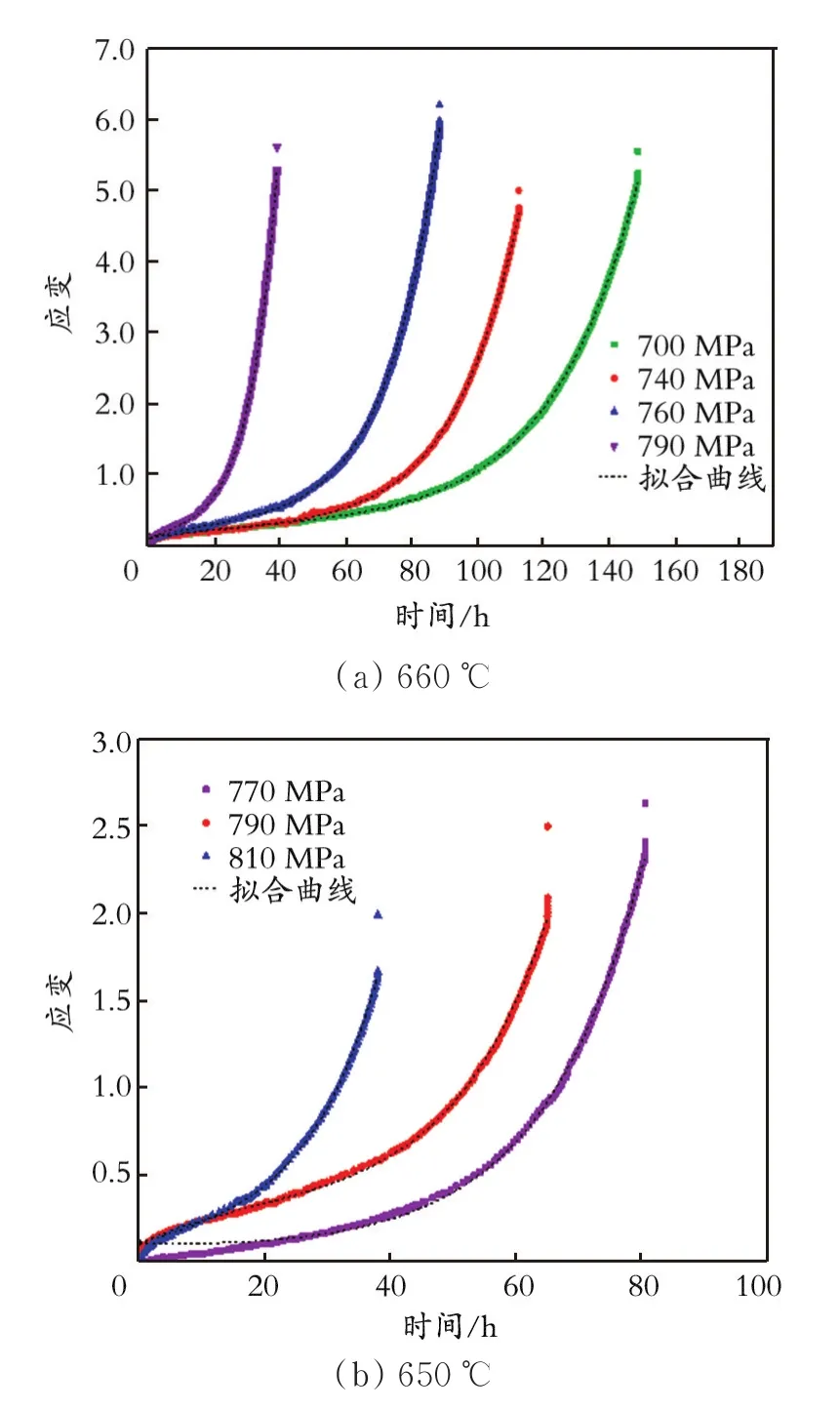
图2 GH4169高温合金在660℃和650℃下的蠕变实验数据及拟合曲线
2.2 修正θ投影法的概念
R.W.Evans等提出的θ投影法所采用的数学模型以Carofalo等式为本构方程[15],即:
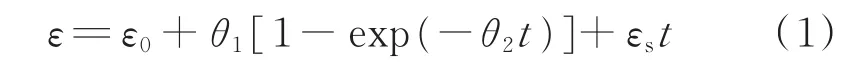
式中,ε0为加载后的初始应变,式中的第二项对应蠕变的第一阶段,第三项对应蠕变的第二阶段;εs为第二阶段的最小蠕变速率;t为时间;θ1、θ2分别为温度应力相关的系数。
式(1)仅仅考虑了蠕变的第一阶段和第二阶段,而θ投影法的基本理论认为,蠕变变形过程是由材料应变硬化与碳化物析出、聚集、孔洞形成及长大引起的材料弱化两部分组成的。应变硬化提高材料的强度,在蠕变的第一阶段得到了充分的体现。应变软化降低材料的强度,主要体现在蠕变的第三阶段。对于蠕变的第二阶段,传统观点认为这是一个稳定状态。事实上,这并不是真正意义上的稳定,而是由应变硬化和应变软化两个过程达到的一个动态平衡。在建立蠕变寿命预测模型时,可以将Garofalo等式中描述蠕变变形的第二阶段,即式(1)中的第三项εs分解为强化部分和弱化部分[16],而且使强化部分与Garofalo等式中的第二项形式相同,而弱化部分代替式(1)中的第三项,由此得到的表达式为:
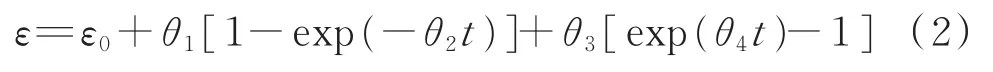
其中,θi(i为1~4的整数)与温度、应力有关,并满足式(3):
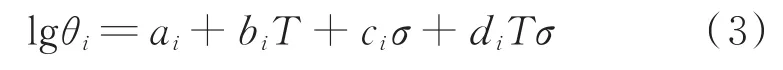
式中,ai、bi、ci、di(i为1~4的整数)是与材料相关的系数,可通过短时蠕变实验数据进行多元线性回归得到;σ为应力,MPa;T为温度,℃。
在恒载荷的条件下,由于蠕变曲线中第一阶段体现并不明显,因此用θ投影法处理可能导致结果不准确。采用修正θ投影法描述恒载荷条件下的蠕变数据,其表达式见式(4),其蠕变曲线主要由蠕变二、三阶段构成[17]。
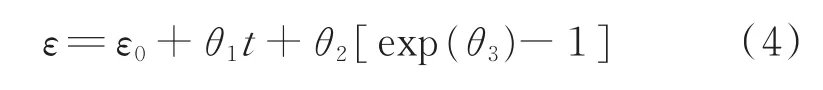
由式(4)得到的与温度、应力相关的参数θ1、θ2、θ3,同样满足式(3)中的温度与应力的相关参数。
本文采用此模型预测GH4169高温合金蠕变的寿命。利用修正θ投影法,对不同应力和温度条件下的GH4169高温合金的恒载荷蠕变曲线数据进行非线性回归。结果表明,该模型能与实验数据较好地吻合,能准确地描述该实验材料的蠕变特性。同时,也可以得到该条件下的θ1、θ2、θ3的值 ,结果见表2。
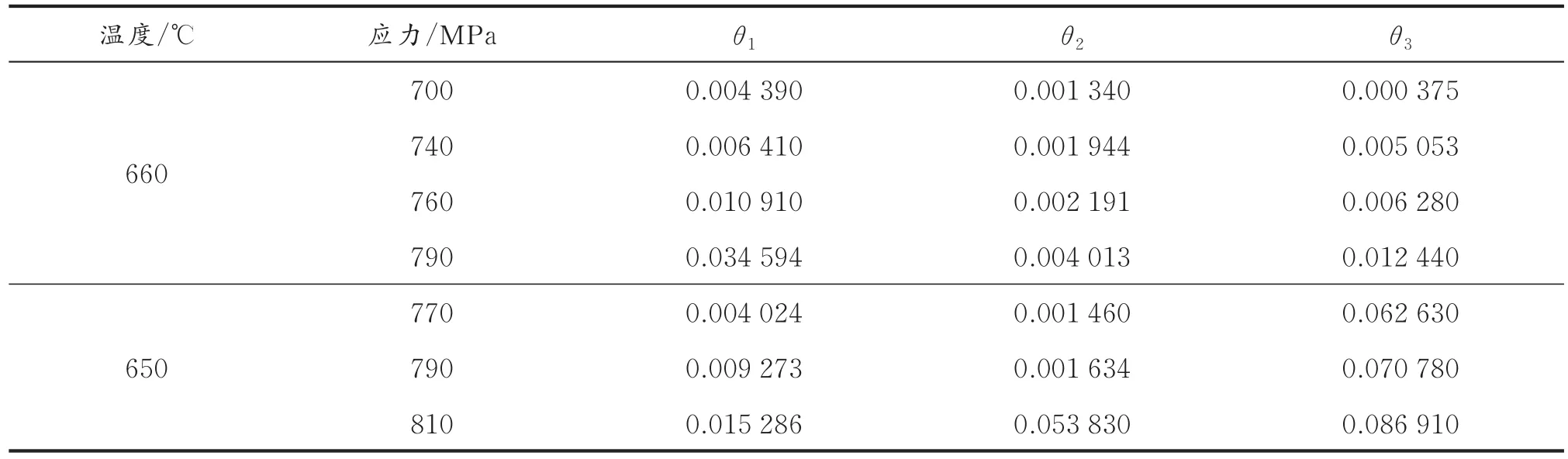
表2 不同温度、不同应力下的 θ1、θ2、θ3
θ1、θ2、θ3和应力、温度的关系满足式(3),修正后的θ投影法能很好地反映各参数的变化规律。将通过式(4)得到的表2中数据代入式(3),进行线性回归可得外推公式的材料参数,结果见表3。

表3 外推公式的材料参数
2.3 修正方程与最小蠕变速率
为了验证修正方程的精度,利用最小蠕变速率的计算值(通过修正的方程求出)与实测值进行对比。对式(4)进行一次求导,可得到应变速率随时间的变化关系,其表达式见式(5)。
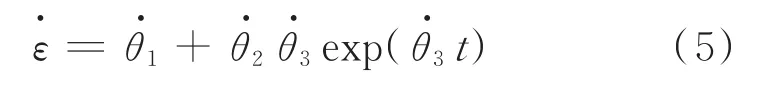
由式(5)可知,当t=0时对应的蠕变速率最小,因此可以得到小蠕变速率:
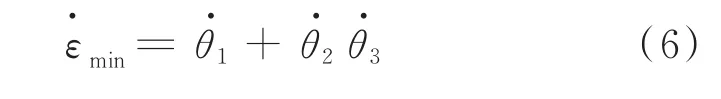
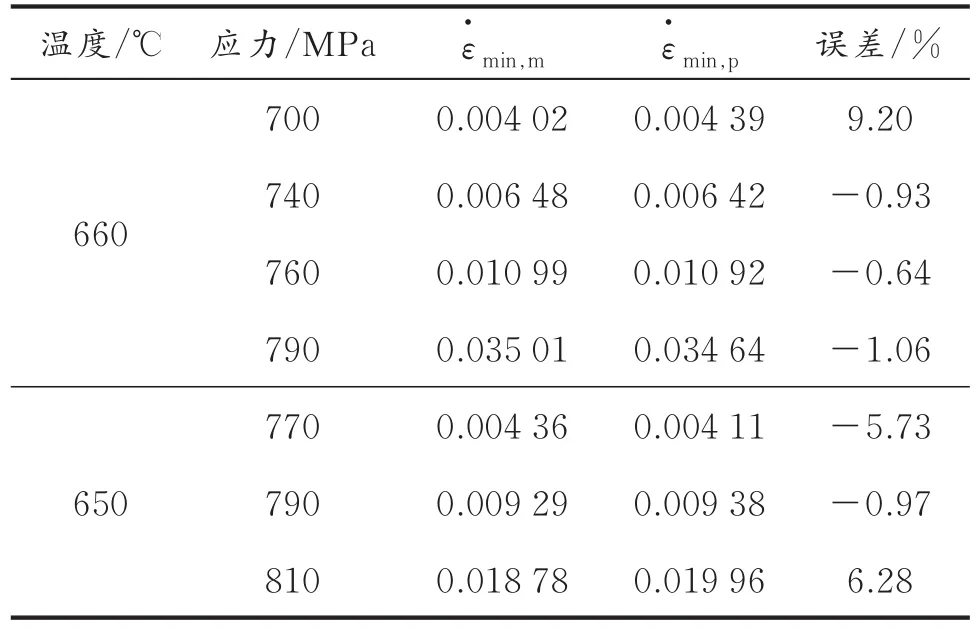
表4 最小蠕变速率的实测值、计算值及误差
2.4 蠕变寿命曲线预测
对修正方程精度进行检验的结果表明,其精度较高,因此将表3中数据代入式(3)中,可得到与温度和应力相关的参数θ1、θ2、θ3,再将θ1、θ2、θ3代入式(4)中,即可得到任意温度和应力下的应变与时间的关系。忽略初始应变ε0,通过任意温度和应力下的应变与时间的关系式,对GH4169高温合金在不同温度、不同压力下的蠕变曲线进行拟合,结果如图3所示。由图3可以看出,蠕变曲线与拟合曲线的吻合度较高,通过图3可以掌握任意应变所对应的蠕变时间。因此,如果已知应变则可知所对应的蠕变时间;如果已知材料的断裂应变就可知材料蠕变断裂时间。通过多组高温高压下的短时蠕变实验值,可得断裂应变的下限。
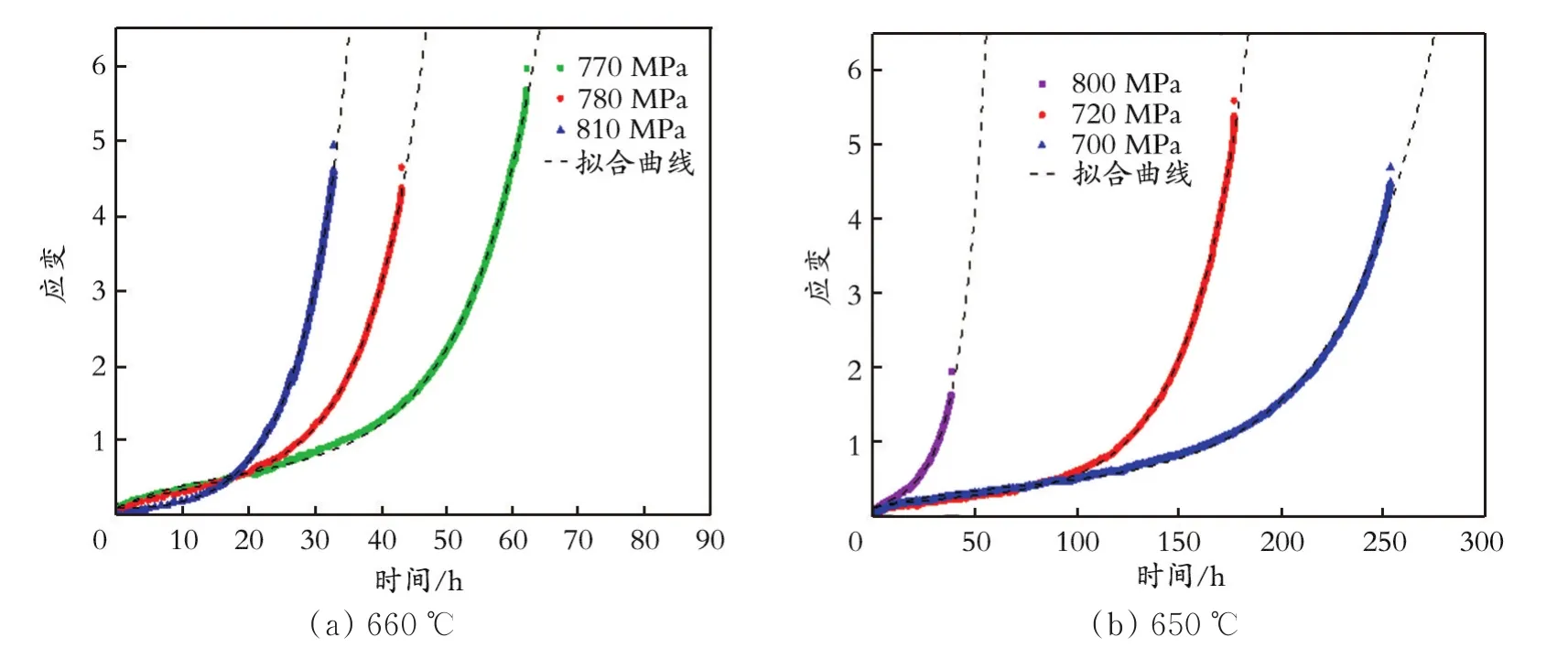
图3 修正θ投影法预测的GH4169高温合金在不同温度及不同应力下的蠕变曲线
B.F.Dyson等[18]根据各种材料的大量的蠕变实验数据,总结了蠕变断裂应变εr的规律,其经验公式为:
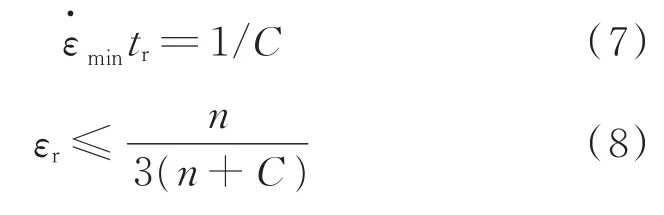
3 结 论
(1)在温度为 660 ℃,应力为 700、740、760、790 MPa及温度为 650 ℃,应力为 770、790、810 MPa的条件下,对GH4169合金进行高温蠕变实验,绘制完整的蠕变寿命曲线。
(2)基于修正θ投影法,建立了GH4169高温合金的蠕变方程,并对所建立的方程求导,计算了不同温度和不同应力下的最小蠕变速率,并与最小蠕变速率的实测值进行了对比。结果表明,最小蠕变速率的计算值与实测值的误差不大,从而验证了方程的预测精度。
(3)通过所建立的蠕变方程,对实验所得的蠕变曲线进行拟合,结果表明拟合精度较高。通过拟合曲线,可求得任意应变所对应的蠕变时间,预测GH4169高温合金在不同温度和不同应力下的蠕变寿命。
