基于改进的双源模型模拟荒漠河岸胡杨林蒸散发

高冠龙,冯 起,刘贤德

1 山西大学,太原 030006 2 陕西省土地整治重点实验室,西安 710064 3 中国科学院西北生态环境资源研究院,兰州 730000 4 甘肃省祁连山水源涵养林研究院,张掖 734000

蒸散发,包括土壤、水体和植物冠层的水分蒸发以及冰雪升华、植物蒸腾等过程[1],是气象、水文和生态学中的重要参数[2],也是植物与环境之间质量和能量交换的重要组成部分[3- 7],其准确量化对于合理制定灌溉方案、提高水资源利用效率具有重要意义[8-9]。直接测定蒸散发的方法主要包括：液流法、波文比法、蒸渗仪法、稳定同位素法、涡度相关法、大孔径闪烁仪法和光合作用仪法等。然而,这些测定方法均是以昂贵的实验设备为基础,且需要专业人员进行维护,人力物力成本均较高[10-11]。通过数学模型进行模拟,从单一气候变量驱动方程到能量平衡与空气动力学原理相结合的方法,可以有效地解决这一问题,近年来得到广泛关注[12]。

目前最常用的蒸散发模型以辐射、温度和能量平衡作为运算基础[13- 15],主要包括：Penman (P)模型、Penman-Monteith(PM)模型、Priestley-Taylor(PT)模型、McNaughton-Black(MB)模型、Shuttleworth-Wallace(SW)模型和Clumping(C)模型等。国内外学者们对于上述各模型的应用非常广泛,研究主要集中于不同模型模拟精度的对比[16- 26]及模型中部分参数计算方法的改进方面[27- 30],以此来提高模型的模拟精度。上述各模型中,PM模型具有模型结构简单、所需参数较少的优点,被认为是理论性最强的蒸散发模型[31],已被广泛应用于农田、森林、湿地等生态系统的蒸散发模拟[32]。然而,PM模型为单源模型,当植被呈斑块状分布或叶面积指数较小时,PM模型的适用性会受到限制。这种情况下,双源SW模型的模拟精度往往较高,但是SW模型结构复杂,包含的参数较多,在参数的准确量化与模拟计算方面存在一定难度。因此,如何改进现有的模型,使其既能够适用于稀疏植被的蒸散发模拟,同时又能在模型结构与参数化方面得到优化,成为了学者们研究的热点。

胡杨是黑河下游额济纳绿洲主要的建群种,也是典型的荒漠河岸林树种,在我国西北地区极端干旱的气候条件下,植被正常生长所需的水分来源主要为地下水,而蒸散发是胡杨散失水分的最主要的途径。关于胡杨蒸散发的模拟研究,Gao等[33-34]分别基于单源和双源模型模拟了黑河下游胡杨林蒸散发,结果显示双源比单源模型具有更高的模拟精度。对于以胡杨为代表的稀疏植被而言,结构较为复杂的双源模型往往更加适用。然而,如何优化模型结构以提升模拟精度这一关键问题仍未得到解决。因此,本文基于改进的双源模型模拟胡杨林蒸散发,这对于弄清胡杨的蒸腾耗水机理、提高水分利用效率具有重要意义。

1 研究区概况

试验地位于额济纳绿洲,大致范围介于99°03′—100°00′E,40°30′—42°30′W,属阿拉善台地的一部分,是黑河末端的大型冲积扇,东为巴丹吉林沙漠,西为马鬃山山地,北到中蒙边界,南到黑河下游上端的鼎新绿洲,绿洲面积3.12×104km2。由西南部剥蚀低山残丘、中东部冲积平原、湖盆洼地与南部巴丹吉林沙漠等组成,海拔在850—1100 m,总地形向东北倾斜；属极端大陆性气候,该地区年均降水量不足 40 mm,最少降水量为 7.0 mm；蒸发量高达 2500—4000 mm,空气相对湿度不足 35%；年均气温 8.6℃,年均风速 4.4 m/s,全年 8 级以上大风日数平均 54 d,盛行偏西风,属极端干旱区。

试验样地位于内蒙古额济纳旗达镇东南的七道桥胡杨林保护区,共有胡杨树80株,为天然纯胡杨林。在该胡杨林保护区内,胡杨树木长势良好,树龄约为32 a,树木平均高度为10.2 m,平均胸径为24.67 cm,平均冠幅为442 cm450 cm。砂质土厚度约为2 m,土壤体积含水量为0.35 m3/m3,土壤容重为1.53 g/cm3。

2 研究方法

2.1 试验设计

试验于2014和2015年胡杨主要生长季内(5月4日—10月8日),在额济纳旗七道桥胡杨林保护区内进行(42°21′N,101°15′E,海拔高度为920.5 m)。在胡杨林中部设有一个24 m高的涡度相关观测塔,塔上安装有一套开路式涡度相关测定系统,探头的安装高度为20 m,该系统由三维超声风速系统(CSAT3)和开路式CO2/H2O红外分析仪(Li- 7500A)组成。除该系统外,一些气象传感器也安装于铁塔不同高度处,包括四分量辐射仪、大气压探测器、空气温、湿度传感器、光合有效辐射仪、雨量筒,土壤热通量板及土壤水分探针分别埋设于地下不同位置及深度处。各仪器的名称、型号、生产厂商、安装高度(深度)、测定参数等信息见表1。

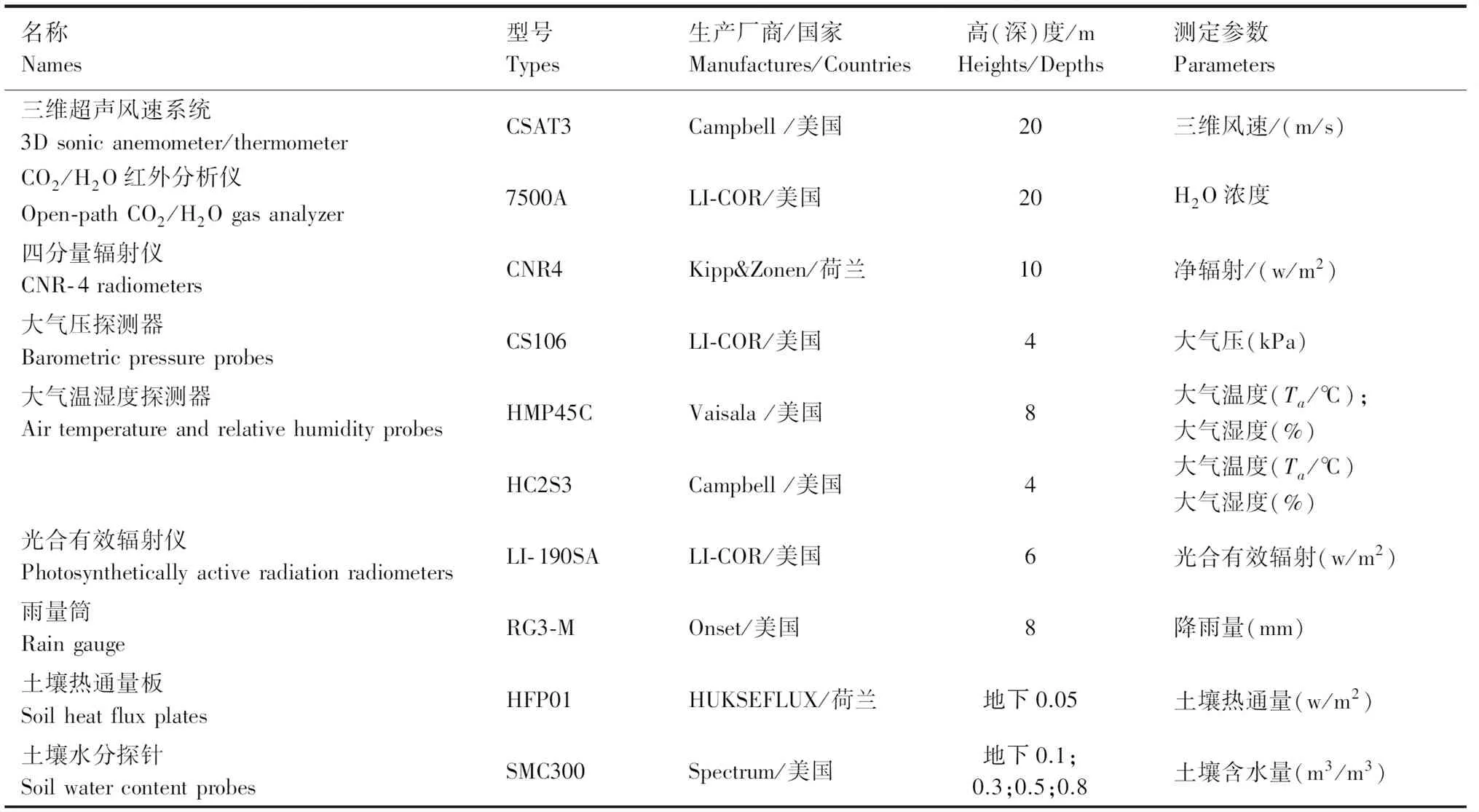
表1 样地内安装试验仪器的相关信息

叶面积指数由植物冠层分析仪(LAI- 2200,Li-COR)测定,每10 d测定一次,于当天的黎明或黄昏时分进行测定。植物冠层分析仪选取10°遮盖冒,首先在没有冠层遮盖的地方读取1个A值,然后在冠层下不同的点位读取4个B值,由此便可计算出LAI数值。重复操作3次,取平均值即为本时间段内胡杨林的叶面积指数。

2.2 数据处理

蒸散发数据由涡度相关系统获取。首先,运用Loggernet 4.0软件对原始数据进行数据分割及格式转换,分割后的数据时间间隔为30 min,格式为TOB1。然后用Eddypro 5.2.0软件对分割后的数据进行基本处理,包括异常值剔除、倾斜校正、时间滞后校正、频率响应校正、超声虚温校正及密度效应校正。对于原始数据(包括脉冲计数与消除、振幅分辨率、信号丢失、绝对限值、偏移度与峰值等)的分析,处理方法均来源于Vickers和Mahrt[35],而对于数据的质量检查则依据CARBOEUROPE标准。经过上述处理后的数据仍然存在异常值,需要再剔除一部分数据,包括降水时次的数据、Rn<10 W/m2的数据以及λET>800 W/m2的数据。

图1 2014和2015年胡杨林能量闭合率Fig.1 Energy balance ratios during the growing seasons of Populus euphratica in 2014 and 2015, respectively

由于仪器自身问题、维护和标定、自然环境条件的限制等原因,一年中通常有17—50%的观测数据缺失或被剔除[36-37]。本试验中,异常值剔除后,有效数据的比例分别为82. 63%(2014)和80.89%(2015)。本文采用的数据插补方法为：2 h以内的缺失数据采用线性内插法插补,超过2 h的缺失数据采用平均昼夜变化法进行插补[38]。鉴于夜间湍流运动很弱,涡度相关数据质量较差,且夜间蒸散发微弱,实际蒸散发取日间时段(8:00—19:00)的蒸散发之和作为全天蒸散发总量,以消除夜间质量差的数据对实际结果的影响。待所有涡度相关数据处理完毕后,可得2014和2015年胡杨林能量闭合率(图1)。

2.3 蒸散发模型介绍

PM模型将下垫面看作一个整体,是单源模型,其公式如下：

式中,ET为总蒸散发,mm/d；λ为汽化潜热,MJ/kg；Δ为饱和水汽压-温度曲线的斜率,kPa/K；γ为空气湿度常数,kPa/K；ρ为平均空气密度,kg/m3；Cp为空气定压比热,J kg-1K-1；D为饱和水汽压差,kPa；u为风速,m/s；rc为冠层表面阻力,s/m；ra为空气动力学阻力,s/m；其余参数意义同上。

SW模型假设作物冠层为均匀覆盖,引入冠层阻力和土壤阻力参数,综合考虑了来自冠层和土壤两个涌源的蒸散发过程,适用于稀疏植被的蒸散发模拟,其计算公式如下：

λET=λEc+λEs=CcPMc+CsPMs

式中,Cs和Cc为分配系数；PMs为冠层下部土壤潜热通量,W/m2；PMc为冠层潜热通量,W/m2；At为总有效辐射能量,W/m2；As为地面有效能量,W/m2；raa为冠层面高度到参考面高度间的空气动力阻力,s/m；ras为地表面到冠层面的空气动力阻力,s/m；rac为单位面积冠层叶面边界层空气动力阻力,s/m；rss为地表面土壤阻力,s/m；rsc为冠层阻力,s/m；Rns为地表净辐射能量,W/m2；其余参数意义同上。

为了有效地平衡PM与SW模型在适用性与参数化等方面的优缺点,可以考虑将PT模型引入PM模型,进而推导出改进的双源(PM-PT)模型。公式如下：

式中,τ=Rns/Rn,αE为受光系数,τc为常数(0.55[27]),其余参数意义同上。

2.4 模拟精度评定指标及敏感性系数

本文引用Legates和McCabe[39]研究中所选用的三个数据指标来评定模型的模拟精度：修正效率系数(E1)、修正一致系数(d1)和平均绝对误差(MAE)。各系数计算公式为：

式中,Oi为实测蒸散发,mm；Mi为模拟蒸散发,mm；Oi为实测平均蒸散发,mm；N为样本总数。如果R2、E1和d1的值较大而MAE的值较小,且斜率接近于1,则该模型模拟精度高。

本文采用Zhan等[40]提出的简便方法以进行敏感性分析：

式中,Sp为敏感性系数,ET0、ET_和ET+分别为各参数值取P0、1.1P0和0.9P0(P0为各参数原始数值)时对应的蒸散发值。

3 结果与分析

3.1 荒漠河岸胡杨林实际蒸散发

3.1.1蒸散发日变化规律

在2014和2015年胡杨主要生长季内,选取生长季初期连续10天(5.4—5.13)的蒸散发实测数据,用以分析蒸散发日变化规律。选择生长季初期作为研究时段的原因在于：5月初胡杨林试验地地表植被还未开始生长,不会对生态系统实际蒸散发产生影响。

由图2可以看出,胡杨林蒸散发日变化大致呈先升高后降低的趋势。上午随着太阳辐射的逐渐增强,气温逐渐升高,蒸散速率逐渐增大,在12:00左右达到峰值。随后,太阳辐射减弱,气温逐渐降低,空气中相对湿度增加,胡杨叶片内外水汽压差减小,蒸散速率随之降低。有些天内蒸散速率在17:00前后还会出现一个峰值,这是由于在这些天12：00—17:00时间段内气温过高致使胡杨叶片气孔关闭。

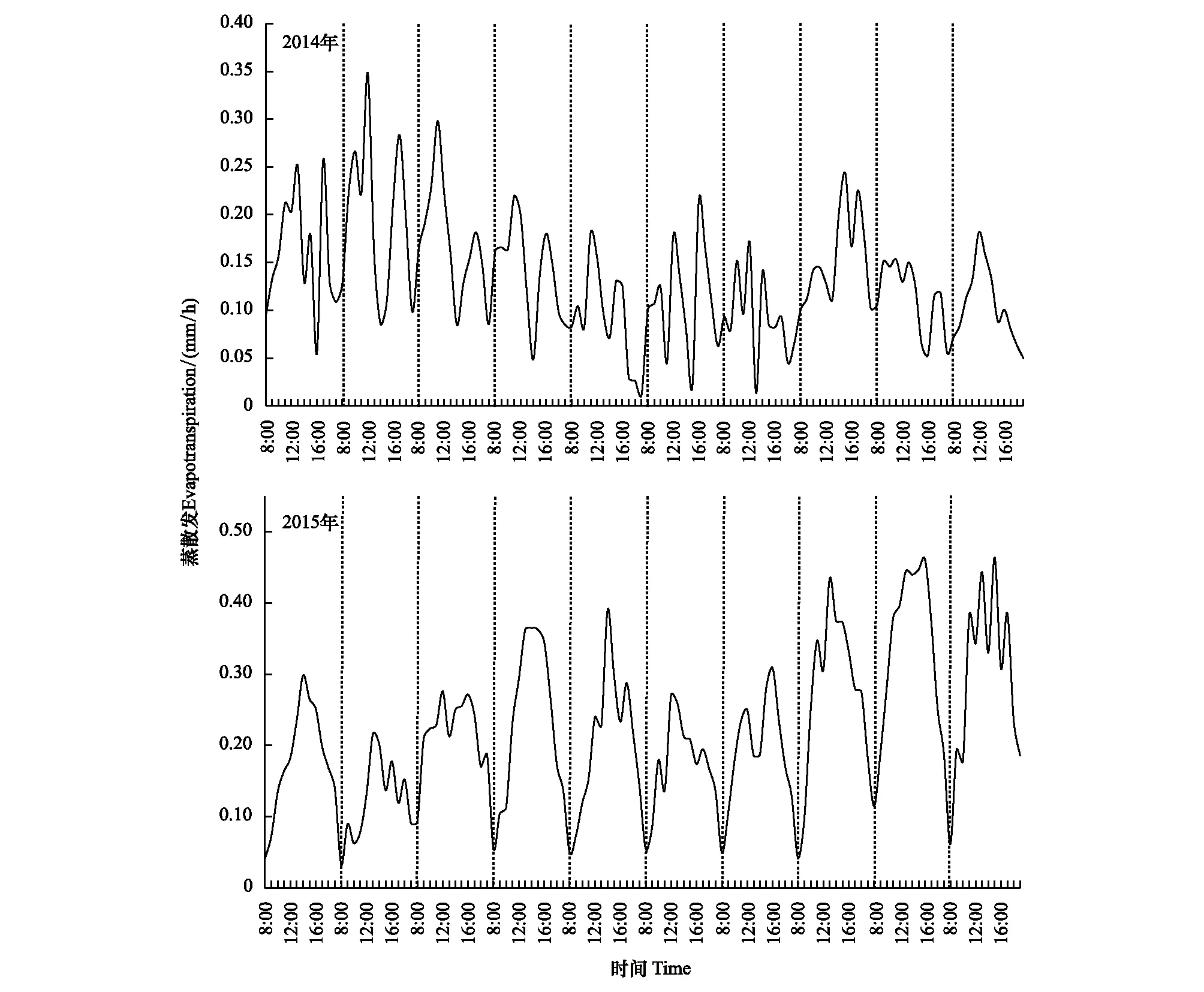
图2 2014和2015年胡杨生长季初期连续10天蒸散发日变化规律Fig.2 Diurnal variations of evapotranspiration during the first 10 days at the early stage of the growing seasons of Populus euphratica in 2014 and 2015, respectively

3.1.2蒸散发各物候期变化规律

2014和2015年试验地胡杨主要生长季及各物候期蒸散发变化规律见图3和图4。可以看出,胡杨主要生长季内蒸散发整体上呈先升高后降低的趋势,2014和2015年生长季蒸散发总量分别为612 mm和658 mm。果期和种子散播期累积蒸散发为生长季内蒸散发总量的主体部分,果期内累积蒸散发分别为316 mm和348 mm,分别占各年生长季蒸散发总量的51.65%和52.87%,平均蒸散发分别为4 mm和5 mm。种子散播期内平均蒸散发略低于果期,2014和2015年胡杨林种子散播期内累积蒸散发分别为261 mm和270 mm,分别占各年生长季蒸散发总量的42.71%和41.12%,平均蒸散发均为4 mm。展叶期和叶变色期内平均蒸散发最低,展叶期累积蒸散发分别为15 mm和23 mm,分别占各年生长季蒸散发总量的2.51%和3.50%,平均蒸散发分别为12 mm和3 mm；叶变色期累积蒸散发分别为19 mm和17 mm,分别占各年生长季蒸散发总量的3.14%和2.51%,平均蒸散发均为2 mm。

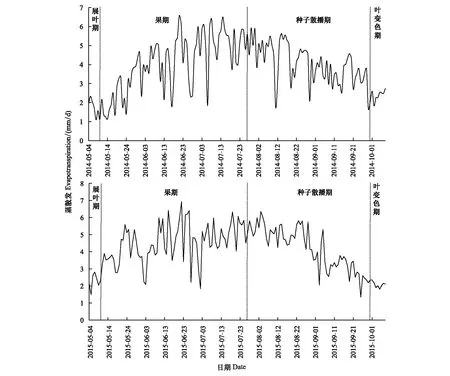
图3 2014和2015年试验地胡杨主要生长季及各物候期蒸散发变化规律Fig.3 Variations of evapotranspiration during the whole growing seasons and each stage of Populus euphratica in 2014 and 2015, respectively

图4 2014和2015年试验地胡杨主要生长季及各物候期蒸散发对比Fig.4 Comparison of evapotranspiration during the growing seasons and each stage of Populus euphratica in 2014 and 2015, respectively

3.2 荒漠河岸胡杨林蒸散发模拟

通过对比实测蒸散发与SW、PM-PT模型模拟的蒸散发结果,进而可确定各模型的模拟精度。2014和2015年胡杨主要生长季实测蒸散发与SW、PM-PT模型模拟蒸散发对比见图5、6和表2。可以看出,2014和2015年胡杨主要生长季内,PM-PT模型其修正效率系数(0.433、0.321)、修正一致系数(0.696、0.629)和决定系数(0.752、0.655)均高于SW模型各系数值(修正效率系数(0.162、0.167)、修正一致系数(0.548、0.542)和决定系数(0.575、0.586)),而PM-PT模型平均绝对误差(0.655、0.746)小于SW模型(0.969、0.916),且PM-PT模型的斜率(0.716、0.616)更接近于1,说明PM-PT模型的模拟效果更好。

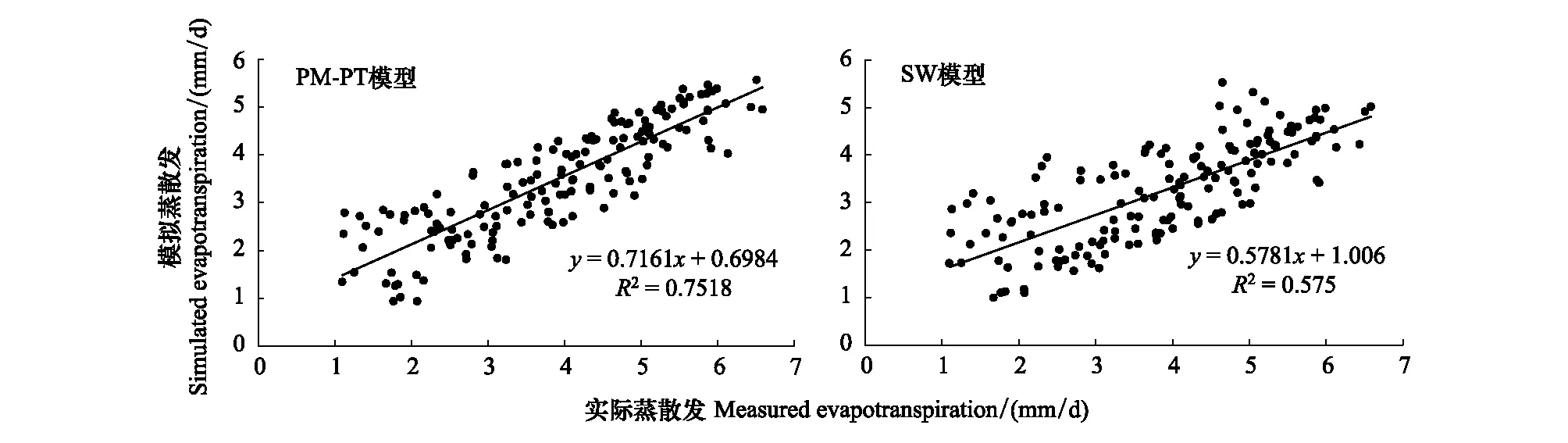
图5 2014年胡杨主要生长季实测蒸散发与SW、PM-PT模型模拟蒸散发对比Fig.5 Comparison between the measured and simulated evapotranspiration of Populus euphratica in 2014

图6 2015年胡杨主要生长季实测蒸散发与各模型模拟蒸散发对比Fig.6 Comparison between the measured and simulated evapotranspiration of Populus euphratica in 2015

3.3 敏感性分析

模型参数的敏感性分析对于量化模型的不确定性至关重要。本文针对模拟精度更高的PM-PT模型对其参数敏感性进行分析,结果见表3。可以看出,2014和2015年胡杨主要生长季内,PM-PT模型对于净辐射的敏感系数值最高,说明模拟蒸散发对净辐射最为敏感。

4 讨论

蒸散发的准确测定与估算对于理解陆-气相互作用及水文过程具有重要意义。从荒漠河岸胡杨林实测蒸散发来看,其日变化大致呈先升高后降低的趋势。上午随着太阳辐射的逐渐增强,气温逐渐升高,蒸散速率逐渐增大,在12:00左右达到峰值。随后,太阳辐射减弱,气温逐渐降低,空气中相对湿度增加,胡杨叶片内外水汽压差减小,蒸散速率随之降低。有些天内蒸散速率在17:00前后还会出现一个峰值,这是由于在这些天12：00—17:00时间段内气温过高致使胡杨叶片气孔关闭。胡杨主要生长季内蒸散发整体上也呈先升高后降低的趋势,果期和种子散播期累积蒸散发为生长季内蒸散发总量的主体部分,展叶期和叶变色期内平均蒸散发最低,原因在于展叶期胡杨叶片尚未完全成形,而叶变色期叶片活性逐渐降低。

表2 2014和2015年胡杨主要生长季SW和PM-PT模型模拟精度对比

表3 基于LAI、Rn、G、D和u的PM-PT模型参数敏感性分析

Sp：敏感性系数,Sensitivity coefficient

对于稀疏植被覆盖条件下的蒸散发模拟,SW双源模型考虑了源自地表的水热通量首先在冠层高度与源自冠层的水热通量相互混合,进而与上方大气相互作用,近年来应用广泛。Hu等[41]基于SW模型,对四个不同试验点的草地生态系统蒸散发进行了模拟,结果表明在日和季节两个尺度上,SW模型模拟精度均较高。然而,SW模型在雨天天气条件下模拟精度有所降低,这主要是由于该模型未考虑冠层截留而产生影响。Zhu等[11]基于SW模型结合贝叶斯方法对青藏高原高山草甸蒸散发进行了模拟,并分析了模型参数的不确定性,结果表明SW模型模拟效果较好。Ortega-Farias等[42]基于SW模型对智利一个葡萄园蒸散发进行了模拟,结果表明在没有水分胁迫的情况下,利用气象和土壤水分数据模拟的蒸散发与实际观测值接近。沈竞等[43]基于SW模型对蒸散发各组分进行了拆分,并采用蒙特卡洛随机参数化方案对模型参数进行了优化。赵丽雯等[44]应用SW模型模拟了绿洲农田玉米生长季的实际蒸散发,并利用涡度相关技术进行了验证。然而,模型结构及所需参数数量均未得到优化。

本研究中,SW模型模拟精度略低,原因在于其模型结构相对复杂,包含参数较多,各参数的准确量化较为困难,而各参数的不确定性往往又导致模拟结果的差异。另外,SW模型的模拟误差可能产生的原因还在于：

(1)SW模型没有考虑土壤和冠层间的反射率和长波辐射。Brenner和Incoll[45]的研究结果表明,冠层和裸露土壤间最大长波辐射差约为100 w/m2；

(2)不同能量来源之间的相互作用会对能量通量产生影响。Ham和Heilman[46]的研究结果表明,约有1/3的感热通量用于了棉花蒸腾。

本文基于改进的双源PM-PT模型模拟了荒漠河岸胡杨林蒸散发,结果显示改进的双源PM-PT模型比双源SW模型模拟精度高,Li等[27]和Sauer等[47]均得出了相同的结论。但是在Li等[27]和Sauer等[47]的研究中,试验均是在土壤水分充足的条件下进行的,而对于极端干旱条件下荒漠植被的蒸散发模拟而言,PM-PT模型的模拟精度还有待进一步验证。本研究以荒漠河岸胡杨林为试验对象,分析了PM-PT模型在蒸散发模拟方面的应用,由于PM-PT模型在模型结构与参数数量方面均得到了优化,因而未来关于PM-PT模型的适用性研究意义显著。

5 结论

本文基于黑河下游额济纳绿洲七道桥胡杨林生态-水文长期固定观测场的实测数据,运用涡度相关技术对胡杨林实际蒸散发进行了观测,通过双源SW和改进的双源PM-PT模型对蒸散发进行了模拟,并将实测数据与各模型模拟结果进行了比较,对比分析了各模型的模拟精度,并分析了模拟精度较高的PM-PT模型的参数敏感性。得到的主要结论如下：

(1)荒漠河岸胡杨林蒸散发日及主要生长季内变化均呈先升高后降低的趋势。从日变化情况来看,蒸散发在中午12:00左右达到峰值。从生长季内变化情况来看,果期和种子散播期累积蒸散发为生长季内蒸散发总量的主体部分,展叶期和叶变色期内平均蒸散发最低；

(2)2014和2015年胡杨主要生长季内,改进的双源PM-PT模型与SW模型相比,在模型结构与参数数量方面均得到了优化,其模拟精度也高于SW模型；

(3)PM-PT模型对于净辐射的敏感系数值最高,说明PM-PT模型对净辐射最为敏感。