步行设施内疏散行人拥挤踩踏仿真研究
2020-07-02刘秋梅武鑫森
岳 昊,刘秋梅,武鑫森
(北京交通大学综合交通运输大数据应用技术交通运输行业重点实验室,北京100044)
0 引 言
随着越来越多大型步行设施的建设,行人拥挤诱发的踩踏事件时有发生,不仅带来巨额的经济损失,还严重威胁人们的生命安全.拥挤踩踏事件具有突发性、危险性、不可再现性等特征,很难获取踩踏事件发生时行人微观动力学方面数据,且组织行人拥挤踩踏实验同样具有一定的危险性.因此,基于微观仿真的行人拥挤踩踏研究,成为行人流领域研究的热点与难点.基于微观仿真,探究拥挤踩踏的生成机理与时空分布等特征,有助于加强行人组织管理,优化空间设施设计,提高行人疏散的安全性与效率性,强化行人疏散安全感.
行人流疏散仿真分为:以社会力为代表的空间连续模型[1]和以元胞自动机为代表的空间离散模型[2].原始社会力模型存在“重叠”“群体特征偏少”等缺陷,后人从随机行为[3]、从众效应[4]、信息传递等角度对其进行改进,但计算复杂、高密度人群仿真精度低的问题依然存在,不适合直接模拟拥挤人群踩踏现象.元胞自动机模型因空间分割相对任意性,用于疏散空间特征、拥挤致伤[5]、人群挤压[6]和行人移动概率[7]等研究.元胞离散空间可以模拟拥挤时人群挤压形变现象,却很难体现行人之间力的微观作用机制.本文采用相互力作用下的空间细化元胞自动机模型,利用元胞自动机空间离散特点,将空元胞作为行人倒地空间,即行人拥挤倒地诱发踩踏的初始条件,构建行人间作用力的传递机制,再现离散空间下作用力的传递过程,达到与连续空间相同的作用力传递效果.在行人拥挤踩踏领域,与以往研究事故触发机理、预防措施等不同,本文从微观作用力角度探究行人踩踏内在机理.
1 踩踏机理
以出口前疏散空间为例.疏散过程中,行人沿着指向安全出口的期望方向移动,在安全出口前产生拥挤排队,每个行人迫切离开危险空间的意愿转化为期望方向上的拥挤力.拥挤力造成行人之间的空间缩小和弹性挤压,还在行人之间传递、累积,形成强大的破坏力;由于行人移动空间急剧缩小,在行人间接触的条件下,拥挤力还会衍生出行人之间的摩擦力,从而降低行人的移动效率,增加行人的拥挤程度.在行人拥挤且竞争移动空间的过程中,拥挤力催促行人移动,摩擦力阻碍行人前进,在拥挤力与摩擦力相互作用下,行人无法按其意愿移动,移动速度大小和方向发生改变.当两者作用力明显加剧时,易使行人移动失败,甚至失控倒地;此时,拥挤行人间相互作用力的平衡态被打破,使倒地者周边行人的受力瞬间失衡,发生相继失控倒地现象;由于倒地信息传递的滞后性,后方行人继续向前拥挤,继而发生连续踩踏现象.
2 仿真模型
2.1 空间与行人
为模拟行人之间的挤压形变现象,仿真模型基于疏散空间细分的元胞自动机构建.根据文献[8],行人在密集人群中占据0.4 m×0.4 m 的方形空间,近似为3×3 个元胞.由于行人可承受的挤压形变程度有限,人体被视为由刚体部分和弹性部分构成,如图1(a)所示.行人刚体部分不可被他人侵占,保证行人在疏散过程中不会发生重叠;行人受力超过一定阈值时,弹性空间可与他人共享,如图1(b)所示.基于空间细分,单位时间步长内,行人的移动领域为以行人为圆心半径为3 个元胞的范围,如图1(c)所示.
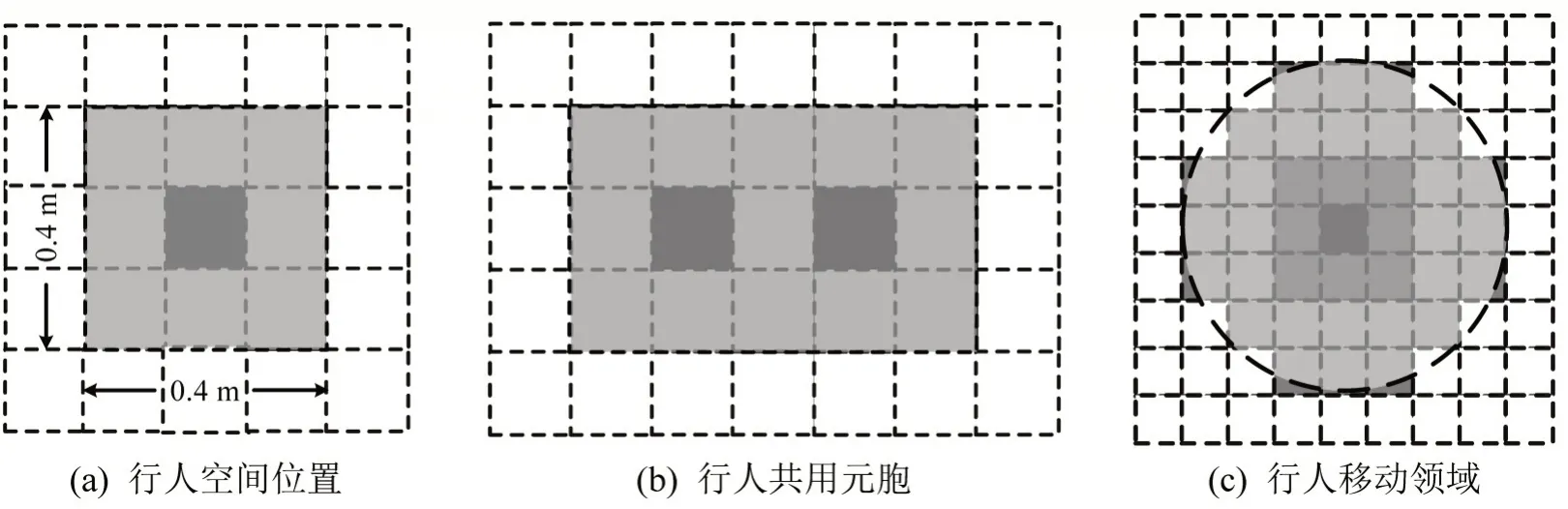
图1 行人边界与移动领域Fig.1 Pedestrian boundary and moving range
当行人移动领域内无空元胞时,移动期望方向指向安全出口;当行人移动领域内有空元胞,且距离出口更近时,为寻求空间舒适性,行人移动期望方向指向空元胞,如图2所示.
2.2 拥挤力产生与更新
由于安全出口的瓶颈效应,行人产生期望方向的移动意愿在拥挤阻滞情况下转化为拥挤力Fn.行人移动选择由移动收益决定,总是朝收益最大的元胞移动,由方向参数和空格参数两部分构成[2],即
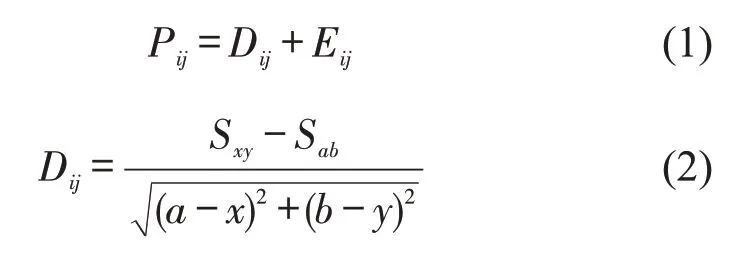
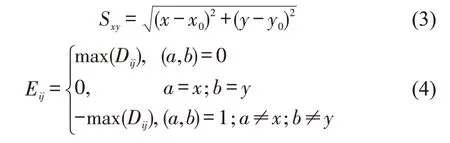
式中:Pij是移动收益;Dij是方向参数;Sxy是点(x,y)到门口距离;Eij是空格参数;(x0,y0)是门口坐标;(x,y)是行人当前坐标;(a,b)是行人目标点坐标;i,j分别表示行人横纵坐标变化量,i=a-x,j=b-y.
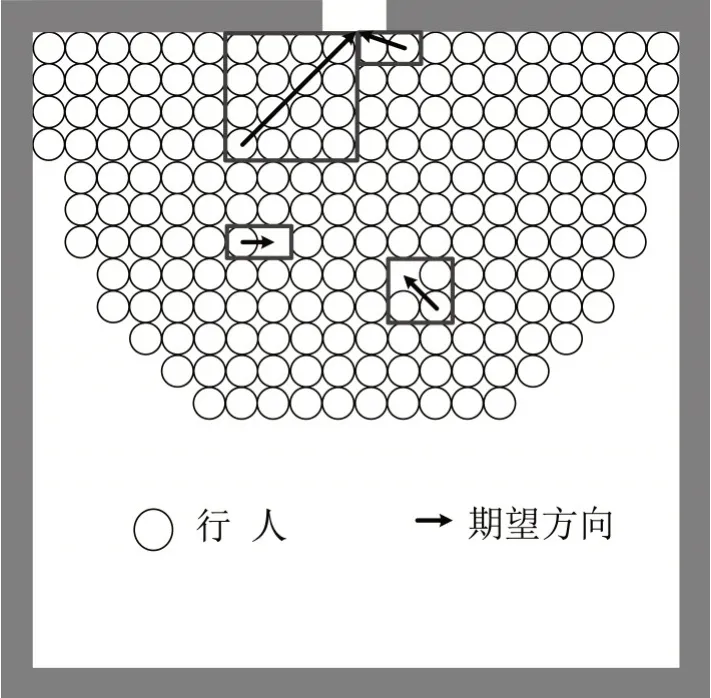
图2 行人期望方向Fig.2 Expected direction
由于行人的异质性,假设拥挤力在0~Fmax间随机分布,Fmax为最大拥挤力.拥挤力的作用效果具有连续性,需要在元胞离散化的基础上再现拥挤力的连续作用效果.在仿真步T=t时刻,行人n的拥挤力为;在t→t+1 过程中,行人n的拥挤力变化量为ΔF;在T=t+1 时刻,理论上行人拥挤力既保留t时刻对受力对象的作用效果,也包含拥挤力变化量的实际作用效果的更新规则为

2.3 拥挤力传递
(1)受力对象.
行人期望方向总是指向出口或距出口更近的元胞,故由行人移动意愿转化而来的拥挤力的受力对象更接近安全出口.模型将行人编号及距安全出口的距离一一对应,按照与安全出口距离的大小从大到小进行遍历.初始时刻第n个行人随机赋值拥挤力,随时间的推进,根据行人拥挤力的变化,计算下一时刻.根据拥挤力方向及行人位置找寻受力对象.受力对象满足两个基本条件:与施力主体接触,距安全出口更近.
(2)拥挤力动态传递分解.
首先,寻找每个行人的受力对象,计算行人当前所受的拥挤力;然后,进行受力分解,直到遍历空间内所有行人.如图3所示.
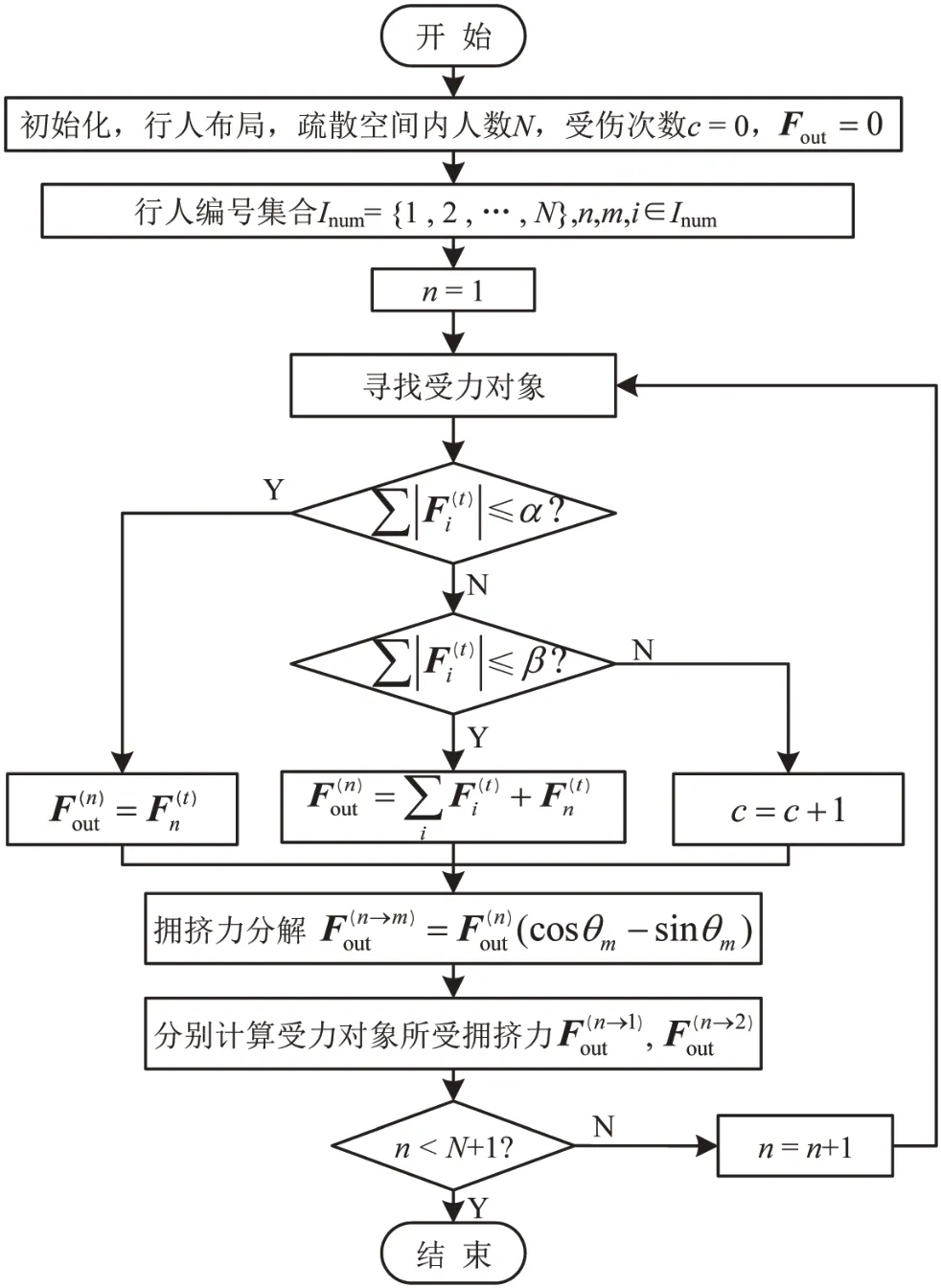
图3 拥挤力传递分解过程Fig.3 Push-force transmission process
图3中,吸收系数α为行人对拥挤力的吸收能力;抗挤伤系数β为行人对拥挤力的承受能力.α和β由行人自身体质、年龄、穿着等决定.为行人输出的拥挤力;为行人n所受拥挤力,i为对n施加拥挤力的行人;为行人n分解传递到行人m上的分力;θm为行人m与拥挤力的夹角.
拥挤力有多个受力对象时,采用距离拥挤力方向最近的原则,将其分解传递给所有受力对象,如图4 所示.拥挤力在传递过程中,由于行人自身弹性吸收作用,会被部分消化.其吸收、传递和分解规则[5]为
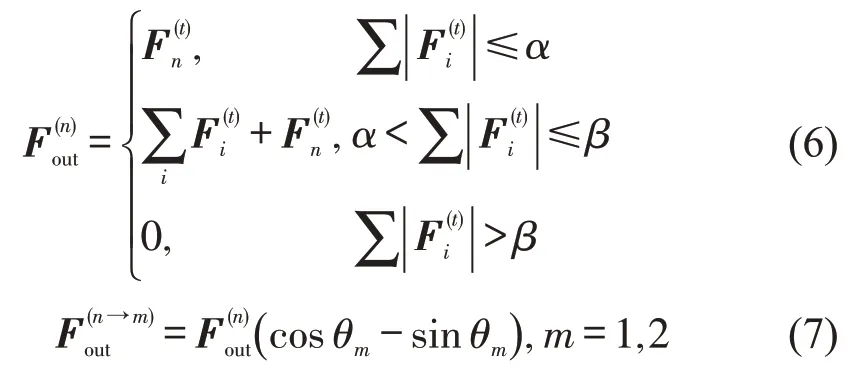
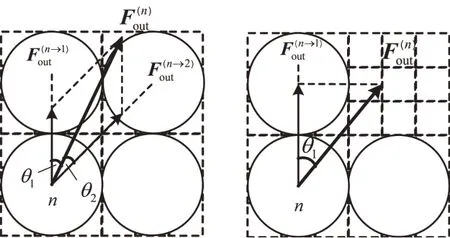
图4 拥挤力分解规则Fig.4 Decomposition rule
2.4 拥挤踩踏
(1)移动阻滞.
行人在拥挤力的作用下产生挤压形变,在移动过程中与他人产生相对速度,进而产生摩擦力.在拥挤状态下,摩擦力不仅阻滞行人向前移动,还可能造成行人移动失败甚至踩踏.行人摩擦力的大小由其所受拥挤力决定,其方向与行人运动方向呈180°,即
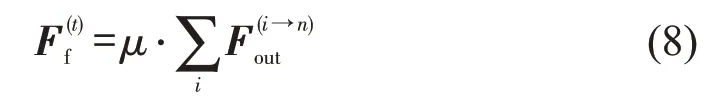
式中:μ为摩擦系数;为行人n所受拥挤力.
(2)踩踏发生机理.
为探究踩踏现象机理,引入抗摩擦系数γ,描述行人对摩擦力的克服作用.根据拥挤力与摩擦力的矛盾程度,判断踩踏事故是否发生.当摩擦力与拥挤力矛盾达到一定值时,人群受力平衡点被打破,弱势群体失控倒地,诱发踩踏.T=t时刻:当时,摩擦力不足以影响行人移动意愿,行人正常移动;当时,行人被迫移动失败.T=t+1 时刻,若行人n再一次被选择进行移动,且所受拥挤力,则该行人失控倒地.行人n的施力主体瞬间受力失衡,相继倒地,直到施力主体受力在自身可承受范围内时,倒地结束,踩踏发生.踩踏事故发生过程如图5所示.

图5 踩踏事故发生过程Fig.5 Process of stampede
行人移动状态为
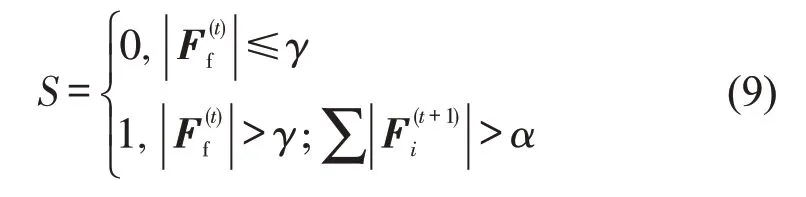
式中:S为行人移动状态,0和1分别表示正常移动和踩踏.
2.5 仿真规则
(1)移动冲突.
若空间内空元胞周围行人满足:移动后不与其他行人重叠,该空元胞在行人可移动范围内,行人不会移动到距离相等或更远的空元胞处,同一时间步内同一行人最多移动一次,则其构成该元胞的待移动行人集,如图6所示.
根据概率选择模型确定最终移动行人.待移动行人集中所有行人竞争元胞空间,并阻碍彼此移动.行人移动概率由自驱动力、拥挤力和摩擦力共同决定.行人所受合力和移动概率为
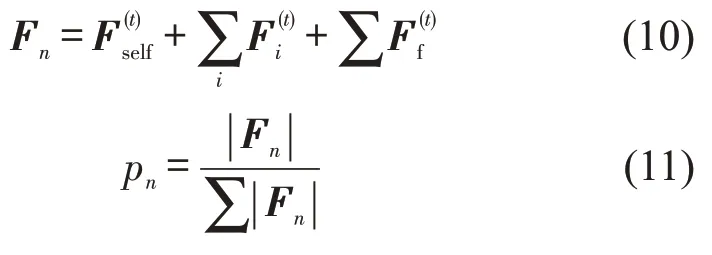
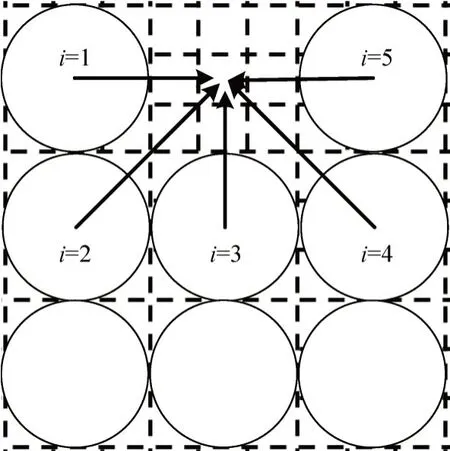
图6 待移动行人集Fig.6 Pedestrians waiting to move
式中:Fn为所受合力;为自驱动力;pn为选择概率.
(2)移动仿真流程.
在行人疏散仿真过程中,首先计算疏散行人受力情况,然后根据行人受力情况进行移动选择,Ns为踩踏行人,Nb为连续倒地行人,Nh为挤伤行人,仿真流程如图7所示.
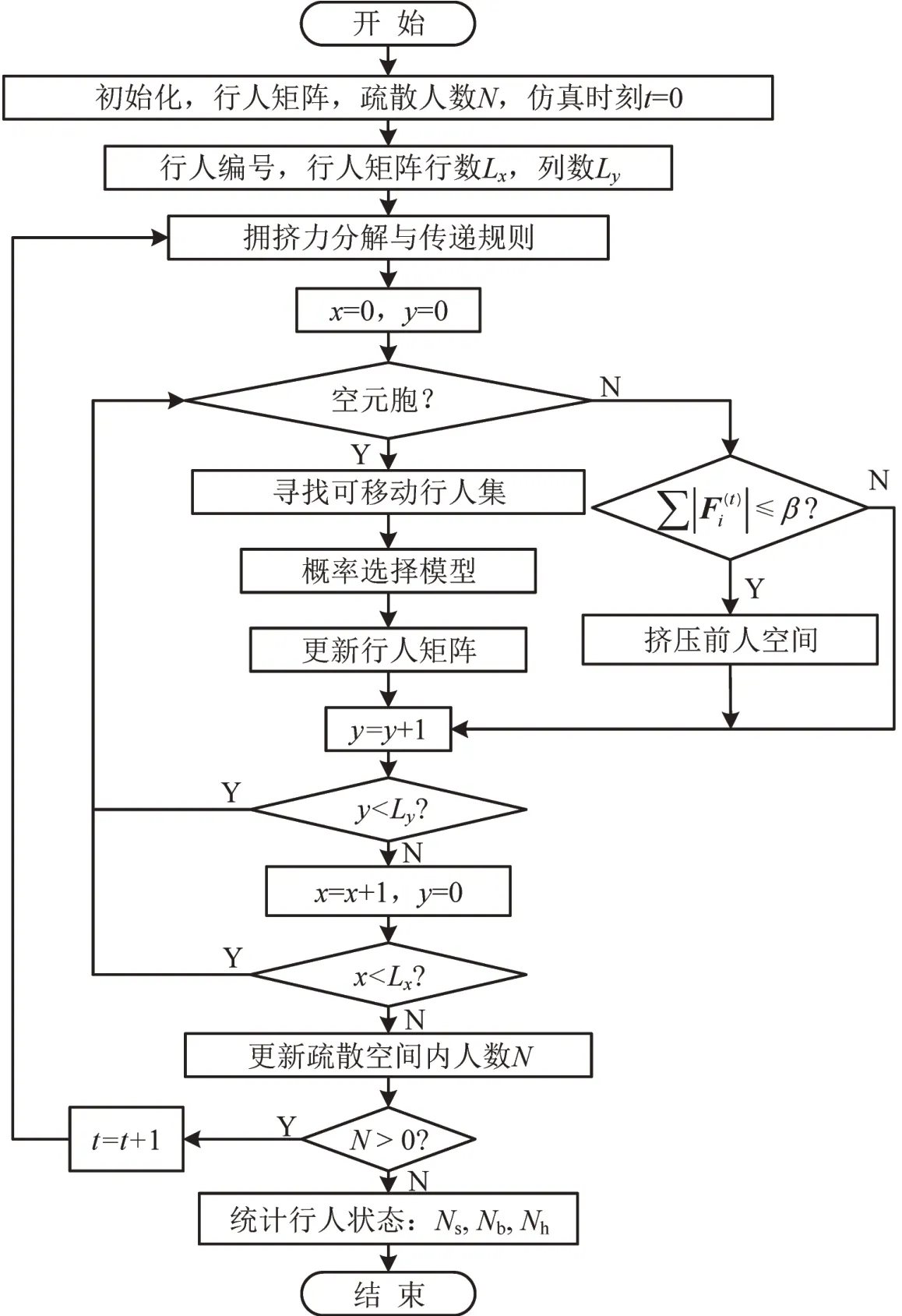
图7 疏散仿真过程Fig.7 Simulation process of evacuation
3 仿真结果分析
3.1 仿真场景
拥挤踩踏往往发生在疏散瓶颈处,疏散人数与瓶颈宽度是主要的预防调控因素.行人拥挤踩踏是有效评价行人组织方案或瓶颈宽度设计合理性的主要指标.在预防拥挤踩踏的实时监控中,主要监控瓶颈前的疏散人数.拥挤踩踏具有局部性、瓶颈处等特点,可在整体设施的基础上,抽象出局部的、单瓶颈、非全局动态的仿真模型.本文以局部的、单出口疏散瓶颈为例,探究行人拥挤踩踏的生成机理,达到预防与保障安全的作用.
仿真场景设置为尺寸8 m×8 m,出口宽度L=0.8 m,占据6个元胞的空间,如图2所示.初始时刻行人呈拱形排列,待疏散行人数量N=202 人,人群密度为0.16 m2/人. 从行人属性出发,假设|Fmax|=100 单位,吸收系数α取[0,160]单位,抗挤伤系数β=170 单位,抗踩踏系数γ取[0,1 800]单位.拥挤疏散时行人步行速度为0.5 m/s,仿真步长为0.8 s.在此基础上,在疏散空间设置4个柱状障碍物,研究其是否影响疏散空间的安全性,如图8所示.
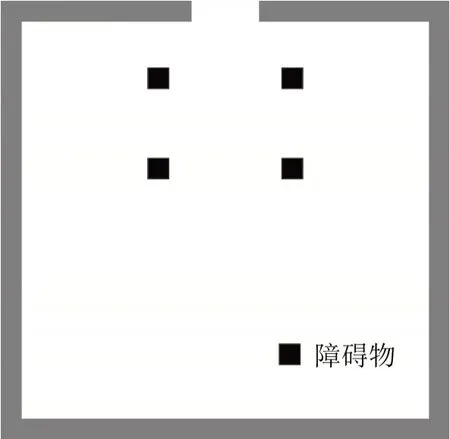
图8 疏散空间布局Fig.8 Layout of obstacles
3.2 行人踩踏情况
图9为N=202,L=6,不同α时,踩踏行人数量Ns随γ的变化情况.当γ增加时,Ns先快速减小,然后缓慢达到趋于0的稳定状态.随着α增加,曲线簇由密集逐渐稀疏,故存在临界吸收系数α1.当α≤α1时,此时α较小,吸收拥挤力的能力较弱,对踩踏人数变化的影响不明显,α的增加不会带来明显的Ns的变化;当α>α1时,此时Ns的大小受α影响十分明显,随着α的增大,Ns下降的速度明显增加.
与无障碍物疏散空间相比,设置障碍物后,踩踏行人的数量明显减少,如图10所示.
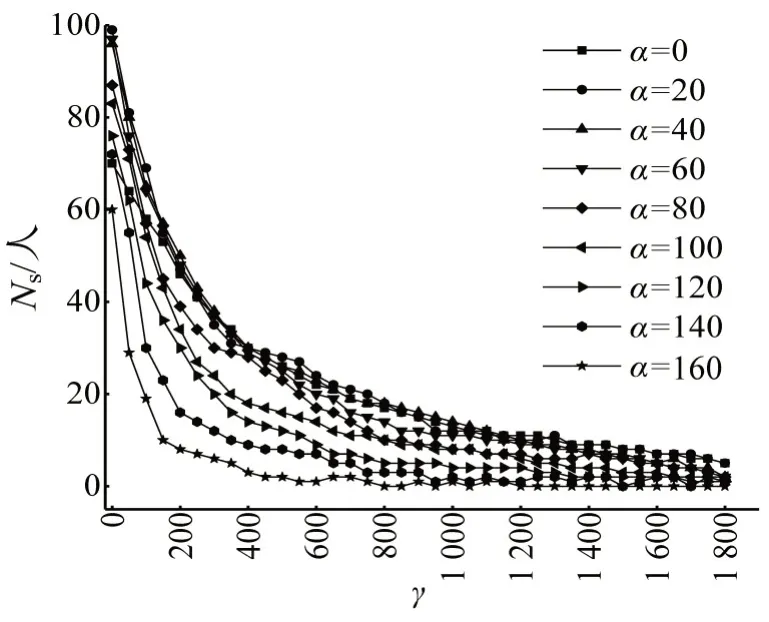
图9 Ns 随α 变化情况Fig.9 Change of Ns with α
当γ在[0,1 800]变化时,总踩踏行人数量sumNs及踩踏与失衡倒地总人数sum(Ns+Nb)随着α的变化情况如图11(a)所示.sumNs随α在[0,160]之间变化时,呈现先上升后下降趋势;当α介于20~40时,达到最大值.sum(Ns+Nb)随着α在[0,160]变化时,呈现单调递减趋势.
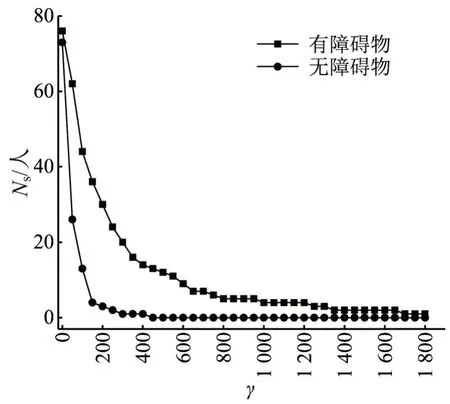
图10 空间布局对Ns 的影响Fig.10 Influence of spatial layout on Ns
Ns随着α的改变呈现先增加后减小趋势,α=20 时出现峰值,如图11(b)所示.此时,拥挤力有一定积聚时间,累积效果达到最大,爆发性更强.当γ在[0,1 800]变化时,Ns对γ的敏感程度逐渐减小,即存在临界值γ1,决定Ns的变化幅度.当γ≤γ1时,随着γ增加Ns迅速减小;当γ>γ1时,随着γ增加Ns保持平稳状态.
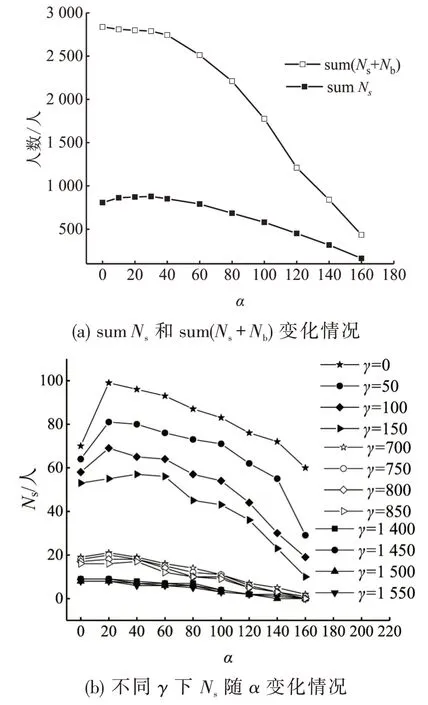
图11 sum Ns 、sum(Ns+Nb) 和Ns 随α 变化情况Fig.11 Changes of sum Ns,sum(Ns+Nb) and Ns with α
γ=700 时,行人挤伤次数随着α增大不断减少,整体分布在[0,50],如图12(a)所示.高挤伤次数出现频率受α变化影响较大,而低挤伤次数出现频率对α变化不敏感.α=40 时,多次仿真得出行人平均挤伤情况,近80%的行人挤伤少于21次,随挤伤次数增加,频率呈现缓慢递减状态,如图12(b)所示.
3.3 踩踏行人时空分布
吸收系数α=120,抗挤伤系数β=170,抗踩踏系数γ=200 时,紧急疏散过程中踩踏行人分布情况如图13 所示.踩踏行人均分布在疏散出口附近区域,时间t=8~20 s 是事故高发时段,其后仅偶尔出现踩踏现象.空元胞需要一定时间才能从门口传递到人群深处,故在疏散初期,后方行人分布还保留初始均匀状态,拥挤力均匀向前传递.随着时间的推进,空元胞逐渐向后移动,行人排列呈现越来越明显的无序化,拥挤力传递呈现不均匀性.局部行人聚集极易造成拥挤力的高度累积,处于拥挤累积链高处的行人有很大概率发生踩踏事故.在t=20 s 以后,部分行人疏离,以及行人踩踏倒地,使疏散空间内行人数量大幅减少,闲暇空间增多,保证行人顺利离开,踩踏事故较少发生.
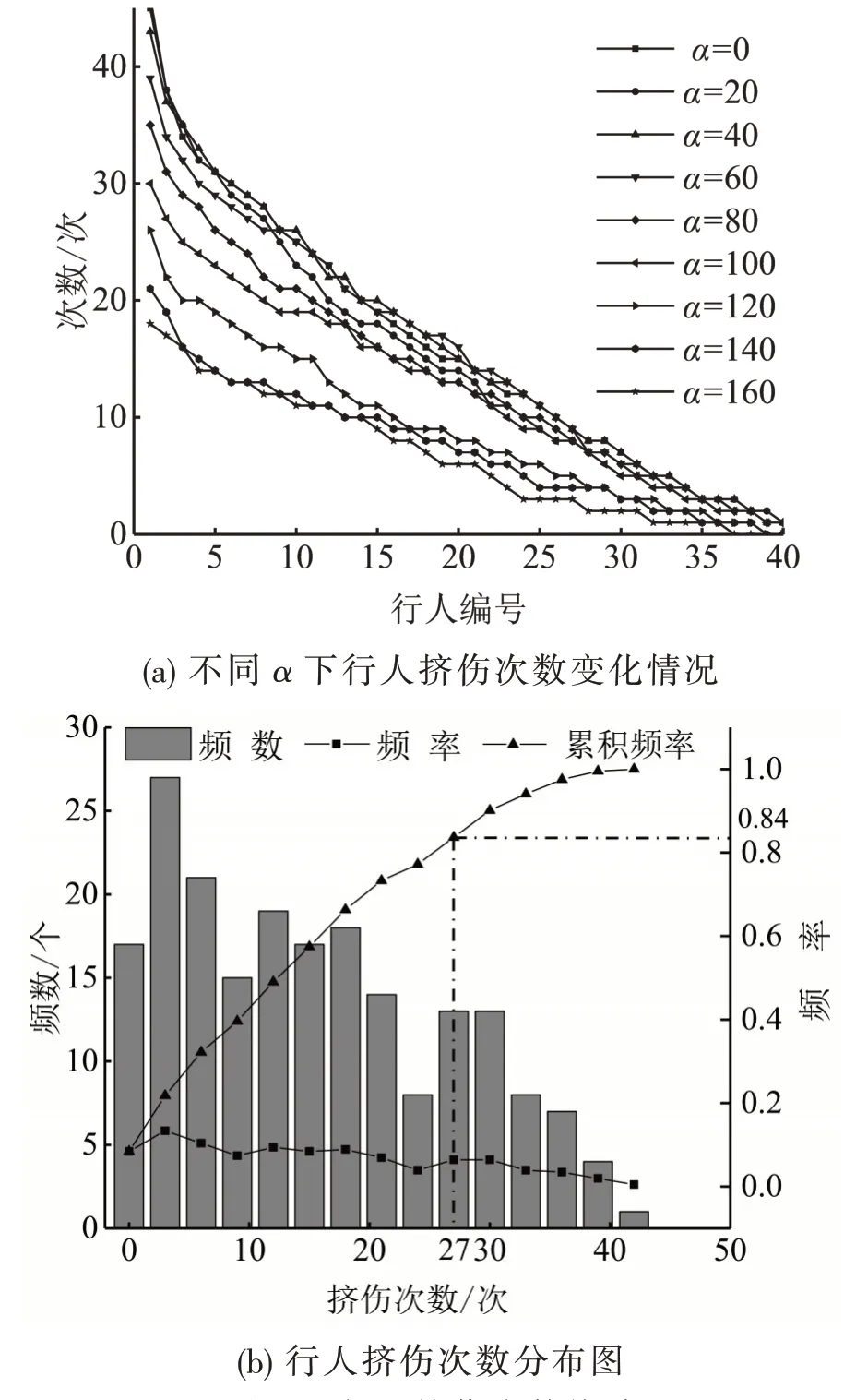
图12 行人挤伤次数统计Fig.12 Statistics of pedestrian injury times
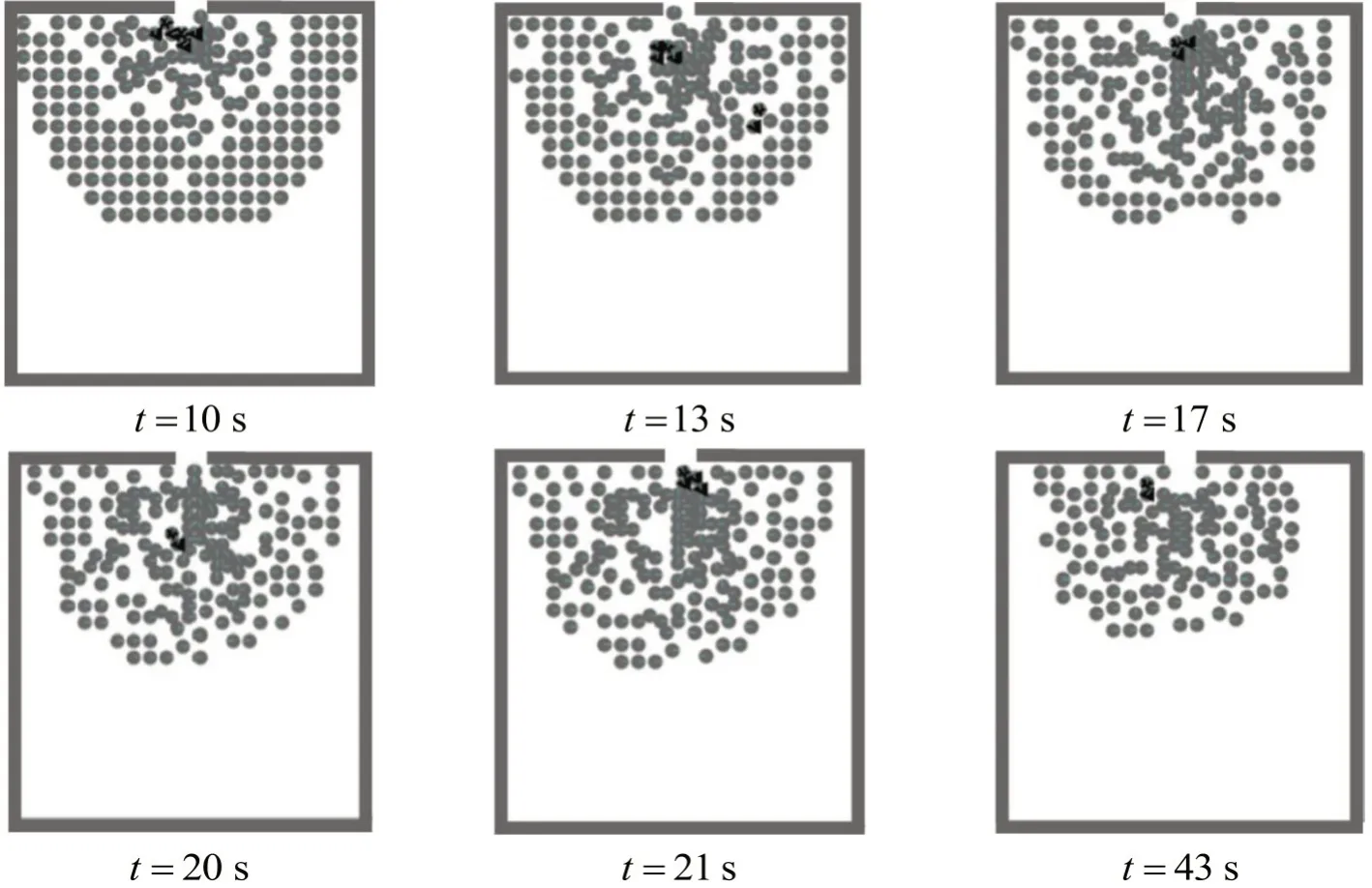
图13 踩踏行人分布图Fig.13 Pedestrian distribution map
4 结 论
通过分析疏散人群间拥挤力和摩擦力的产生与作用机制探究踩踏发生机理.将连续与离散模型相结合,搭建力作用下的元胞自动机模型,再现行人拥挤踩踏现象.通过建立拥挤力的吸收、传递、摩擦力的产生与作用、行人概率选择、事故发生等规则进行行人踩踏现象仿真.研究发现:当多个行人竞争同一疏散空间时,局部人群矛盾冲突达到最大;当所受拥挤力和摩擦力超过安全阈值时,行人容易失控使局部受力失衡进而发生拥挤踩踏.在疏散瓶颈前设置障碍物,能有效中断拥挤力的传递,减少拥挤踩踏发生.行人安全阈值越高外界拥挤力作用效果越低,拥挤人群稳定性越高.因此,步行设施可以通过提高疏散空间安全系数和行人安全阈值避免踩踏,为事故防范提供建议.仿真结果发现,疏散出口前是拥挤力高度聚集区,拥挤踩踏空间上呈现环出口集中分布现象,时间上具有一定滞后性.本文模拟再现了行人拥挤踩踏现象,但未能有效再现实际拥堵中行人晃动现象,后续研究进一步挖掘行人拥挤力间的作用机理,再现拥堵晃动行人作用力的聚集效应.
