基于3DCNN-DNN的高空视频交通状态预测

彭 博，唐 聚，蔡晓禹，谢济铭，张媛媛，王玉婷

(1.山地城市交通系统与安全重庆市重点实验室，重庆400074；2.重庆交通大学交通运输学院，重庆400074)

0 引 言

随着社会经济的发展和城市机动化进程的快速推进，交通拥堵已成为国内外城市发展的焦点问题，有效识别和预测道路交通状态是减少城市交通拥挤、避免交通瘫痪的基础与关键.为此，许多城市基于感应线圈、视频检测器、RFID和浮动车等技术感知交通信息，其中，视频检测器在城市交通监控中应用十分广泛，根据视频识别预测交通状态将显著提升交通信息可视分析精准程度及交通管控效果.

交通状态识别方面，基于单帧图像的交通信息提取与交通状态识别的研究较多，Quiros[1]基于模糊逻辑提出视频图像交通状态识别方法，崔华[2]利用模糊C均值聚类算法对静态图像进行交通状态识别.这些方法对单张图像识别效果较好，但没有考虑帧图像之间的时空信息.2013年，Ji[3]构建的三维卷积神经网络(3DCNN)，可有效提取视频时空信息，从此3DCNN 在视频行为识别领域备受关注，C3D、R3D、R(2+1)D等3DCNN模型也相继出现[4]，使得直接基于视频进行交通状态识别成为可能.

交通状态预测方面成果也十分丰富，主要有时间列预测、回归预测、机器学习预测等方法.Wang[5]利用非参数回归分析方法建立了交通运行状态预测模型，Sun[6]提出基于支持向量机(SVM)的交通状态预测方法，Xu[7]基于ARIMA 和卡尔曼滤波实时预测道路交通状态，Huang[8]利用GPS 轨迹数据提出了基于LSTM 的交通拥挤预测模型.这些方法大多基于浮动车数据、地磁微波检测数据及RFID轨迹数据等展开研究，利用视频进行交通状态预测的研究较少.

综上，3DCNN 可同时学习时空特征，有望实现视频交通状态识别.对于视频交通状态预测，由于预测结果为有限的交通状态类别，可将预测问题转化为分类问题，常用的分类算法有SVM、线性分类、DNN分类模型等.考虑交通状态的时空非线性变化特征及DNN 深度学习的优势，本文基于3DCNN 识别视频交通状态，构建交通状态预测DNN模型，并建立数据集进行测试分析.

1 方法简介

以道路交通高空视频为实验数据，构建基于3DCNN与DNN的交通状态预测方法，主要由3个部分组成，如图1所示.

图1 方法流程Fig.1 Method flowchart

2 基于3DCNN的视频交通状态提取

3DCNN利用δ×w×h(δ为深度，w为宽度，h为高度)的三维卷积核直接对具有深度G(图像帧数)、宽度W(帧图像宽，单位为pixel)、高度H(帧图像高，单位为pixel)三个维度的视频进行卷积运算，同时提取图像空间信息及相邻图像之间隐含的时间信息.C3D是一种经典的3DCNN模型[4]，在UCF101和Sports-1M数据集的数百种视频动作行为(化妆、跳高、滑雪等)识别中准确率高达85.2%，能有效识别视频行为趋势.交通拥挤或畅通可以理解为一种视频行为，故基于C3D 展开视频交通状态识别的探索性研究，为后续交通状态预测提供数据支撑.

建立基于C3D 的视频交通状态识别方法，如图2 所示，路段交通视频Λrd为输入，输出C种交通状态的概率p1～pC，视频交通状态Θrd取概率最大值对应的状态.视频处理过程采用C3D 网络结构，包括8 个Conv 卷积层、5 个Pool 池化层、2 个fc全连接层和一个softmax输出层，所有卷积层使用3×3×3的三维卷积核，池化核为1×2×2或2×2×2.

图2 基于C3D 的交通状态识别Fig.2 Traffic state recognition based on C3D

C3D 视频处理的关键在于三维卷积，原理如图3 所示. 任意交通视频Λrd含有g帧图像(G=g)，即f1～fg.以Conv1 为例，采用δ×w×h的卷积核每次对δ帧图像(fi,fi+1,…,fi+δ-1 ，i≤g-δ+1，其中，i表示图像帧序号)的w×h范围进行卷积运算，沿着单帧图像滑动卷积步长μ1=1，深度方向卷积步长μ2=1，直至将g帧W×H的图像范围全部运算完毕.Conv2 继续应用δ×w×h的三维卷积核对Pool1得到的三维特征矩阵进行卷积运算，以此类推，最终输出到全连接层进行状态类别划分.

图3 三维卷积原理Fig.3 Principles of 3D convolution

3 基于DNN的交通状态预测模型

3.1 DNN模型构建

ϒ′时段的道路交通状态预测问题可转化为以Φ为输入，CD种交通状态为输出的分类问题.Φ的第r行为(Θr1,Θr2,…,ΘrD)，表示第r时段整个道路的交通状态，φr为交通状态变量，φr=(状 态1,状态2,…,状态CD).则有

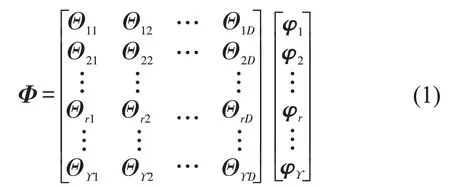
构建以向量(φ1,φ2,…,φϒ)为输入的DNN交通状态预测网络模型，如图4所示.输入层有ϒ个神经 元，第l个隐藏层有Ωl个神经元，l∈{0,1,2,…, }L，输出层有ξ个神经元，最终获得ϒ′时段的道路交通状态，=(状 态1,状态2,…,状态CD).

DNN 相邻网络层之间采用全线性连接结构，为解决复杂的非线性问题，需要在隐藏层引入合适的激活函数.本文构建的神经网络结构较为简洁，采用ReLU 激活函数保障训练效果及收敛速度，获得各神经元之间的权重系数及输出值.

图4 DNN 交通状态预测模型Fig.4 DNN traffic state prediction model

DNN输出层引入softmax分类函数，将多个神经元的输出映射到(0,1)区间，选取概率最大的作为预测结果.

式中：Sq表示输出层第q个神经元的概率值；aq表示输出层第q个神经元的初始值；ξ为输出层神经元总数，即道路交通状态类别总数.

3.2 DNN预测模型优化

研究和经验表明，DNN 网络性能主要受到神经元数量(影响学习能力)、隐藏层深度(过少可能无法捕获数据非线性特征，过多可能导致过拟合)、训练批大小(过小时难以收敛，过大容易出现内存溢出、收敛缓慢)等影响.针对交通状态预测任务，本文对神经元数量、隐藏层数量和训练批大小进行交叉实验，从而确定合理的网络结构，测试方案如表1所示.

经测试发现，隐藏层取4 层，神经元数量分别取64、128、128、64，训练批大小取64的时候模型结构最佳，详情见5.2节.

表1 DNN 结构优化测试Table 1 Optimization tests of DNN structure

4 实验数据与环境

4.1 实验数据

实验原始数据为分辨率为1 920 pixel×1 080 pixel的道路交通高空视频，分别制作交通状态识别数据集和预测数据集.

(1)交通状态识别数据集.

将高空视频平均划分成D个路段，取D=3；各路段视频切分为ms/段，取m=5；形成路段的单元交通视频，人工分为畅通与拥堵两类(C=2).由于畅通和拥堵状态的视频特征较明显，为提高模型收敛速度并保障识别效果，构建样本量N1=64的训练集Q1，样本量N2=140 的测试集Q2，如图5所示.

图5 交通状态识别数据集Fig.5 Data sets for traffic state recognition

(2)交通状态预测数据集.

利用训练好的C3D模型提取道路视频连续ϒ个时段的交通状态序列Φ=(φ1,φ2,…,φϒ)，取ϒ=12；将第ϒ+1 段的道路交通视频实测状态作为Φ的标签值，每一组Φ和对应的形成一个供DNN 训练测试的样本.整个道路交通状态有CD=23=8 种，即BBB，BBG，BGB，BGG，GBB，GBG，GGB，GGG，其中，B、G分别对应路段交通状态为拥堵、畅通.对应构建训练集Q3和测试集Q4，样本量如表2所示.

表2 交通状态预测数据集样本量Table 2 Datasample sizes for traffic state prediction

4.2 试验环境

实验平台为64 位win7 工作站，配置VS2013+CUDA8.0+Anaconda2 等环境，搭建了Pytorch 和tensorflow深度学习框架，采用Python3.6作为编程语言.

5 模型训练与测试分析

5.1 模型训练

对视频交通状态的C3D模型训练，基于数据集Q1采用SGD随机梯度下降法更新网络权重，学习策略Step方式，即每隔s轮迭代调整一次学习率β.

式中：β0为基础学习率，取0.000 1；γ为学习率的变化率，取0.1；f(·) 为向下取整函数；t为当前迭代轮数，共100轮；s为衰减步长，取10.

对于DNN模型训练，基于数据集Q3对各个备选模型进行10 000 轮迭代训练.训练过程中将预测结果与真实标签进行比较，以交叉熵损失值最小为目标对网络权重参数进行微调，直到模型损失值收敛，损失函数为

式中：ψ为损失值；yq为输出层第q个神经元对应的状态类别标签值.

在反向传播更新每一层网络权重参数的过程中，使用Adagrad 自适应梯度下降算法，通过约束学习率更新网络权重.

式中：Γt、Γt+1分别为第t、t+1 轮迭代的网络权重矩阵；η为全局学习率，取0.05；ρτ为第τ轮迭代时的梯度，τ为迭代轮数编号，分别取1,…,t；ε为平滑项，取10-7.

5.2 模型测试分析

基于测试数据集Q2，对C3D进行测试验证并计算准确率、召回率和F1值[9]，结果如表3所示，畅通和拥堵状态识别平均准确率为95.86%，平均召回率为95.71%，平均F1值为95.71%，测试效果如图6所示，其中，Pr为判定概率.可以看出，C3D模型可准确有效提取视频交通状态.

表3 C3D 测试结果Table 3 C3D test results (%)

图6 C3D 识别效果Fig.6 C3D recognition results

基于测试集Q4，测试实验方案中每个DNN模型，结果如图7所示.可以看出：每层神经元数量取100 时，达到预测准确率峰值；隐藏层取4 时，预测准确率最高，为81.37%；训练批大小取65时，预测准确率最高，为90.20%.

图7 DNN 优化测试结果Fig.7 DNN optimization tests

由于计算机为二进制结构，为提升模型性能，将神经元数量和训练批大小调整为2的幂次方，隐藏层神经元数量可选64 或128，训练批大小选64.经过多次组合试验，提出优化模型DNN*，推荐结构及参数如表4所示.

表4 DNN＊模型结构及参数Table 4 DNN＊model structureand parameters

5.3 模型对比分析

基于测试集Q4，将DNN*模型与K-Means、KNN、SVM、线性分类[10]、DNN 线性分类[10]进行测试，对比验证模型性能，如表5所示.

可以看出，针对视频交通状态预测任务，DNN*准确率为91.18%，比DNN 线性分类高6.86%，显著优于K-Means、KNN、SVM 和线性分类.此外，DNN 线性分类准确率比线性分类高36.27%，说明DNN 结构更适用于交通状态预测任务.

基于Q4的测试结果进行Radviz 可视化分析，如图8所示.可以看出：①K-Means、KNN、SVM和线性分类模型的GGG 交通状态与图8(a)相比，预测效果较差，总体上劣于DNN*与DNN线性分类；②图8(b)、(e)整体上差别不大，但图8(b)左上部分空心正方形与图8(a)更一致，说明DNN*比DNN线性分类对GGG 交通状态预测效果更好；③图8(a)、(b)数据分布几乎一致，表明DNN*预测结果与实际状态相符.

表5 模型预测准确率Table 5 Model prediction precision (%)

基于测试集Q4将DNN*预测结果与真实结果进行对比，如图9 所示.可以发现，在204 个样本中，DNN*有18个样本预测错误，BBB和BGG状态预测效果略差，但总体上预测结果与真实状态基本对应.后续研究可进一步扩大训练样本或者改进模型结构.

图8 预测结果对比Fig.8 Prediction results comparison

图9 DNN*预测效果Fig.9 DNN*prediction effects

6 结 论

本文构建了基于3DCNN-DNN的视频交通状态预测通用模型，对城市道路交通视频状态进行识别与预测.将视频行为动作识别的3DCNN引入到交通视频状态识别领域，可直接对交通视频进行三维卷积，准确获取各时段不同路段的视频交通状态矩阵.构建DNN 短时交通状态预测模型，具有多隐藏层深度学习的优势，预测准确率优于K-Means、KNN、SVM、线性分类及DNN 线性分类模型.

由于交通场景的复杂多样性，以及构建大规模交通视频深度学习数据集的困难性，本文在构建有限数据集的基础上进行了3DCNN-DNN视频交通状态识别与预测的探索性研究，对模型架构及参数优化验证等方面有待进一步拓展研究.