基于地层旋转的地层视倾角计算新方法——应用于水平井地质导向

解 飞 王 蕴 梅俊伟 陈贞龙

中国石化华东油气分公司勘探开发研究院

0 引言

天然气勘探开发过程当中，常采用水平井、大斜度井来增加轨迹在目的储层的穿行长度，以此增加产能。地质导向正是应用随钻测量工具获取钻头近处地层最新地质资料，来不断修正钻前地质认识，使轨迹尽可能穿过最佳储层的有效方法[1]。尤其随着页岩气开发工作的逐步深入和开发规模的不断加大[2-5]，如何更精确地进行地质导向，指导钻井轨迹的调整，使水平轨迹在优质储层段穿行，对地质导向方法技术提出了迫切要求[6]。

王谦等[7]以测井资料为基础，建立井眼轨迹与储层界面在钻进方向上的数学关系，对地层厚度变化的储层实时预测井眼轨迹与储层边界的距离，但对倾向倾角多变的地层效果不佳。李林等[8]的“探层测距”方法可以精确地测量钻具到储集层边界的距离，实现地质导向的功能。闫振来[9]研究出了一种从测井曲线中提取出小层对比信息的方法，然后利用极值方差聚类自动分层进行目的层层位和岩性的对比，并研发出了水平井地质导向测量参数随钻解释系统。孙金浩[10]指出三维地质模型能有效地提高钻井效率和随钻地层评价的精度。费世祥等[11]利用三维地震和地质建模对储层空间展布进行预测，形成“小层精细对比入靶、地质小尺度、地震大方向”的综合导向技术。地质导向过程中，通过钻前收集井区地质构造图、已钻井测录井数据、井区地震剖面图等来建立地质模型[12-15]，可以预先计算地层倾向和倾角。但是往往由于受到地震资料或邻井测录井资料的品质或数量限制，无法较精确地获得目的层着陆点地层视倾角。要实现井轨迹大位移穿越目的层，地层视倾角作为一项重要参数，直接关系到钻井轨迹的实时调整，影响到该井是否能实现地质目标[16]。孙斌[17]给出了基于等厚对比原则的地层视倾角以及入靶垂深预测计算方法，根据不同地层结构采用相应的入靶轨迹控制方式。在涪陵以及南川地区的页岩气水平井地质导向中，普遍采用这种邻井对比方式的地层视倾角实时计算方法。

笔者针对入靶前的地层视倾角计算提出了一种地层旋转方法，将地层视倾角的计算转化为一个全局寻优问题。同样是基于地层对比原则，新方法可以在靶前大角度扭方位且地层倾向未知，以及所选取标准井与水平井钻遇地层的铅垂厚度差别大且地层真厚度未知，这两种情况下稳定有效地计算地层视倾角。并提出了适用于新方法的二阶段法，可以在计算地层视倾角的同时计算出地层综合倾向和真倾角，尤其适用于井网稀疏和地震资料缺乏的低勘探程度区域。

1 水平段地层视倾角计算原理

在水平井的钻进过程当中，通过邻井对比实时计算地层视倾角所遵循的原理是地层等厚对比原则，即假设地层在沉积形成过程中是稳定的，其地层真厚度基本保持不变。这一原则对于沉积环境稳定，横向分布均匀的海相沉积地层具有广泛的适用性。选取合适的导向对比标准井，仔细对比随钻伽马数据、岩屑、气测等资料并在实钻水平井上找到与标准井所对应的特征点，是精确计算地层视倾角的关键。

1.1 常规几何方法

1.1.1 地层真倾角一致且方位摆正

当所选取的标准井是水平井的导眼井或离水平井距离较近时，地层产状稳定的情况下，其地层真倾角基本一致。如图1-a所示，当井轨迹的方位摆正后（井底方位角与水平段设计方位角一致），水平段地层视倾角（α）为：

式中α表示水平段地层视倾角，(e)，当α为正值时，表示沿钻进方向地层下倾，反之，则上倾；hvd表示在水平井上选取两个特征点的垂深之差，m；Δh是标准井上所对应的两个特征点的垂深差，m；Δx表示两个特征点在水平面投影上的距离，m。

1.1.2 地层真倾角一致且方位未摆正

受地面条件的影响，一些水平井在造斜段需要大角度扭方位，在入靶前其方位角甚至仍未达到水平段的设计方位。那么，利用公式（1）所计算的地层视倾角，实际上代表的是实钻方向的地层视倾角（α′）（图1-b）。当地层倾向已知时，地层真倾角（αt）计算公式如下：

其中

式中αt表示地层真倾角，(e) ；α′表示实钻方向的地层视倾角，(e)；ω′表示实钻方位与地层倾向之间的夹角，(e)；x、y、z分别表示辅助计算的中间量，m。

通过地层真倾角可以求得水平段地层视倾角为：

图1 常规水平段地层视倾角计算图

其中

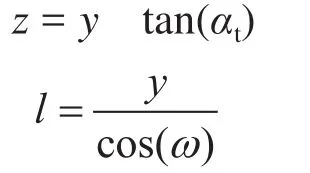
式中ω表示地层倾向与水平段方位之间的夹角，(e)。

1.1.3 地层真倾角差别较大

以上两种水平段地层视倾角的求取方式是建立在地层真倾角差别较小的基础上，当地层因构造运动剧烈等因素，导致选取的标准井与水平井所钻遇地层真倾角差别较大时，以上公式计算会产生较大的误差。如图1-c中所示，两段地层在铅垂方向的垂深差Δh1和Δh2的差距较大，公式（1）的计算方式不再合适。当地层真厚度（ht）已知时，若方位已摆正，则水平段地层视倾角为：

式中β表示两特征点连线与水平面的夹角，(e)；γ表示两特征点连线与地层面的夹角，(e)；L表示两个特征点在空间上的距离，m。

若方位没有摆正，则由公式（2）、（3）继续求取水平段地层视倾角。

1.2 基于地层旋转方法

通过在三维空间中对地层进行旋转，即在水平面上不断改变地层倾向，以及在垂直方向不断改变地层真倾角，来计算水平段地层视倾角（图2-a）。该方法把地层视倾角的计算问题转化为一个全局寻优的过程，借助计算机的计算能力，采用遍历的求解方式求得水平段地层视倾角。实现步骤如下所述。

1）如图2-a所示，在实钻的水平井上确定几个特征点A0，A1，…，An，其中n≥2（至少选取3个特征点）。

2）在所选取的标准井上确定对应的几个特征点a0，a1，…，an，其中n≥ 2（图 2-b）。

3） 计 算a1，…，an分 别 到a0的 垂 深 差 值a1a0，…，ana0。

4）地层倾向在区间[0，360e）以及地层真倾角在区间[0，αmax]各自以一定间隔连续变化，其中αmax为设定的最大地层真倾角。不断计算A1，…，An到过A0的地层界面的铅垂方向距离A1A′1，…，An A′n（图 2-b）。

5）由等厚对比原则易知，当地层倾向和真倾角的取值与地下实际地层的倾向和真倾角一致时，有并以此作为判别准则求出地层倾向和真倾角。

6）将地层倾向与真倾角代入公式（3）中可以计算出水平段地层视倾角。

图 2-c 给出了步骤 4）中A1A′1，…，An A′n的计算方法，由公式（2）可知，实钻方向地层视倾角为：

An A′n的求取方式与公式（6）相同。

式中E表示目标函数；Aave表示数列的平均值；std表示求标准差运算。

目标函数取最小值时，可以求得地层倾向与真倾角。由图2-b可以看出，这种目标函数可以从原理上有效削弱标准井与水平井所钻遇地层真倾角差别较大时，给水平段地层视倾角计算带来的影响。地层旋转法计算流程如图3所示。

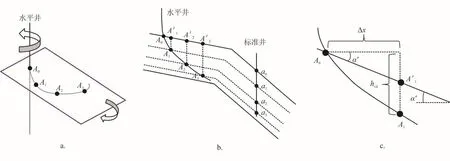
图2 地层旋转法计算水平段地层视倾角图

本文井眼轨迹计算方法采用的是最小曲率法[18]，但是受到工程上测量误差以及计算数据本身精度等因素影响，尽量选取大角度扭方位的井段更有利于寻找全局最优解。所以实际应用时，对于大角度扭方位的情况采取二阶段法：①阶段一。选取大角度扭方位的井段，此时选取的井段较长，利用全局寻优得到地层整体的倾向和真倾角，然后计算水平段地层视倾角。②阶段二。选取邻近钻头的特征点，此时选取的井段较短，将地层倾向设为阶段一中求得的地层倾向，只在区间[0，αmax]内连续改变地层真倾角，计算出精度更高的当前阶段地层视倾角。

2 现场测试

图3 地层旋转法计算流程图

为了验证本文提出的基于地层旋转的水平段地 层视倾角计算方法的有效性，针对摘要中新方法的两个主要优势，分别采用下面两个实际资料测试的例子加以论证说明。

2.1 JYX1井水平段地层视倾角计算

JYX1井位于川东高陡褶皱带万县复向斜南部的平桥南斜坡，主要目的层为上奥陶统五峰组—下志留统龙马溪组下部页岩。龙马溪组下部龙一段可以划分为①—⑨小层，其中①—③小层具有高TOC、高孔渗、高含气、中高硅质含量特征，利于水平井钻探和压裂，是页岩气勘探的甜点段。

JYX1井水平段设计方位为200°，在③小层中部入靶。地质导向过程中，选取邻近的标准井进行地层对比计算地层视倾角，图4是JYX1井的地质导向图。从图4中可以看出，自A点后井眼轨迹才达到水平段的设计方位200°，此前经过了大角度扭方位过程。B点是方位角摆正后最近的GR值反转点，该井深处对应的井斜角为94.5°，由此可知实际水平段地层视倾角为－4.5°（正值表示下倾，负值表示上倾，下同）。JYX1井周围已经有多口完钻井，由此绘制的构造图如图5所示。图5中黑色箭头可以读出入靶前地层倾向约为54°。

图4 JYX1井地质导向图

图5 JYX1井目的层构造图

采用地层旋转法的二阶段法计算地层视倾角，所涉及主要信息如表1所示。

1）阶段一。选取龙一段⑨—③小层（井深3 720～4 030 m）上的GR特征明显（波峰或波谷）的点作为特征点，这些特征点在实钻轨迹上方位角范围为163°～188°。设定地层倾向在0～360°内以 1e为间隔连续变化，地层真倾角在0～10°内以0.1e为间隔连续变化，图6-a是以这两者为自变量得到的目标函数图形。图6中A点处是目标函数的全局极小值，对应的地层倾向为62°，地层真倾角为5.0°，进而计算得到水平段视倾角为－3.72°。

2）阶段二。将阶段一中计算得到的地层倾向62°作为固定输入，只在0～10°内以0.1°为间隔连续改变地层真倾角。为了计算出精度更高的当前阶段地层视倾角，特征点的选取范围为龙一段④—③小层（井深3 900～4 030 m）。图6-b是目标函数随地层真倾角变化情况，在B点处目标函数值最小，此时地层真倾角为6.4°，可以计算出水平段视倾角为－4.77°。

表1 二阶段法计算地层视倾角表 单位：(e)

图6 二阶段法目标函数值图

从以上计算结果可以看出，阶段一中计算得到的特征点井段地层的综合倾向为62°，与从构造图上读出的入靶前地层倾向54°比较吻合，为阶段二精确计算水平段视倾角提供了基础。阶段二计算的水平段视倾角－4.77°，也与地质导向图上得到的实际水平段地层视倾角－4.5°极其吻合，说明了本文基于地层旋转的地层视倾角计算方法在大角度扭方位情况下的有效性。值得注意的是，图6-a中二维目标函数值大体上是以所选取的特征点方位角范围163°～188°对称分布（并非真的对称）。方位角范围越窄，这种对称性越是明显，甚至造成全局极小值点的多解性，这也是阶段一中特征点选取大角度扭方位井段的原因。

2.2 DSX1井地层视倾角计算

DSX1井位于川东高陡褶皱带万县复向斜平桥背斜南部，目的层位为下二叠统茅口组下部茅一段。茅一段可以继续划分为①—⑨小层，其岩性主要为深灰至浅灰色厚层状灰岩及生屑灰岩。

图7 连井对比图

DSX1井的水平段设计方位为165°，其靶前与水平段基本位于一条直线，方位已经摆正。图7是DSX1井的连井对比图，除了DSX1井外，还有本次计算所选取的两口标准井DSX1-1和DSX1-2井。其中，DSX1-1是DSX1井的原导眼井，而DSX1-2井则离DSX1井平面位置相对较远。表2为两个标准井茅一段⑧—⑥小层的视厚度对比，小层视厚度比值是DSX1-1各个小层视厚度与DSX1-2井对应小层视厚度的比值。比值均约为0.7，反映了造成视厚度差距的原因是由于两处地层真倾角差别较大。

表2 标准井小层视厚度对比表

如表3中所示，新方法特征点选取井段为茅一段⑧—⑥小层，方位角已经摆正，所以只需水平段视倾角在－10°～10°内以0.1°为间隔连续改变即可。相当于直接进入阶段二，以水平段倾向代替地层倾向，则水平段视倾角替代了地层真倾角。因此，两个标准井情况下，目标函数随水平段视倾角变化如图8所示，图中两个极小值点（A、B点）所对应的水平段视倾角分别－4.0°和－5.1°，两者非常接近。另外，使用DSX1井的导眼井DSX1-1作为标准井时，基本符合地层真倾角一致且方位摆正的条件，利用常规几何方法中的公式（1）计算地层视倾角为－3.88°，但是标准井选DSX1-2井时，计算结果为－15.57°，两者差异巨大。

以上计算可以看出，当所选取的标准井恰当时（如DSX1-1），新方法和常规几何方法所计算出的地层视倾角非常吻合，可以当作准确值作为参照。但是当地层真倾角不同导致标准井的铅垂厚度与实钻水平井差异较大时，常规几何方法在不知地层真厚度的情况下，无法稳定、准确地计算地层视倾角。相反，新方法在这种条件下仍然适用，体现了其对标准井的选取具有更强的适应性。

表3 不同标准井的地层视倾角计算表 单位：(e)

图8 不同标准井计算的目标函数值图

3 结论

本文提出了一种在三维空间对地层进行旋转来求取地层视倾角的方法。以地层等厚对比原则为基础，将地层倾向和地层真倾角作为自变量，构建目标函数。把地层视倾角的计算转化为全局寻优问题，有效克服了常规计算方法中一些情况下的苛刻条件：要求地层倾向或地层真厚度已知。通过原理分析与实际资料测试，得出如下认识：

1）在靶前大角度扭方位的情况下，新方法通过二阶段法的阶段一可以计算得到的特征点井段所钻遇地层的综合地层倾向和真倾角，继而由阶段二精确计算水平段视倾角。

2）新方法的目标函数从原理上削弱了，因标准井与水平井钻遇地层的铅垂厚度差别大对地层视倾角计算的影响，体现了该方法对标准井的选取具有更强的适应性。

另外，在全局搜索过程中，为了避免二维目标函数陷入局部极小值，应该尽可能增大阶段一中计算地层倾向所选取的特征点方位角范围。