Novel approach for active vibration control of a flexible missile

Cheng-long Pn , Ji-li Rong ,*, Tin-fu Xu , D-lin Xing

a School of Aerospace Engineering, Beijing Institute of Technology, Beijing 100081, China

b Norinco Group Aviation Ammunition Research Institute, Harbin 150030, China

c Beijing Institute of Astronautical Systems Engineering, Beijing 100076, China

Keywords:Flexible missile PID controller Active dynamic vibration absorber Genetic algorithms

ABSTRACT This paper investigates the feasibility of using an active dynamic vibration absorber (ADVA) for active vibration control of a flexible missile system through simulation. Based on the principles of a dynamic vibration absorber (DVA), a ring-type ADVA is first designed to attenuate the elastic vibration of the flexible missile, and the design of the active controller adopts the proportional-integral-derivative (PID)control algorithm. The motion equations of a flexible missile with an ADVA, which is subjected to follower thrust at its aft end, are derived using the Lagrangian approach. Taking the minimum of the root mean square(RMS)of the lateral displacement response of the center of mass as the objective function,a genetic algorithm (GA) is used to optimize the parameter of the DVA and PID controller. The numerical calculations show that the ADVA and DVA are effective in suppressing the vibration and provide approximately 41.2%and 17.6%improvement,respectively,compared with the case of no DVA.The ADVA has better performance than the DVA. When the missile is subjected to follower thrust, the effect of vibration reduction is more effective than the case without follower thrust. It is feasible to reduce vibration and improve the stability of flexible missiles by means of the ADVA.

1. Introduction

To achieve the tactical and technical requirements of long range,high precision and high maneuverability, missiles are slender and long.The use of a light composite material and a thin wall structure impart these missiles obvious with prominent elasticity. The rigid body model does not satisfy the needs of technology development.Beal [1] investigated the stability of a flexible missile under constant and pulsating aft thrusts and then analyzed the influence of the control system on the critical thrust. Platus [2] idealized an elastic missile as a simple beam model and derived the equations of motion and the aeroelastic stability equation of a flexible spinning missile. Xie et al. [3,4] derived the aeroelastic equation of a nonspinning and nonuniform beam under follower thrust. The transverse vibration, dynamic stability and flutter characteristics of a flexible missile with constant thrust are discussed. Li et al. [5]calculated the trajectory and vibration characteristics of a spinning flexible launch vehicle. Xu and Rong et al. [6,7] considered the effects of spin, thrust, and aeroelasticity to idealize an elastic spinning missile as an unconstrained flexible rotor model and analyzed the stability and dynamic response of the flexible spinning missile under thrust. Shi et al. [8,9] investigated whether aeroelasticity affects the dynamic stability of the coning motion of a spinning missile. Hua et al. [10] investigated the effect of elastic deformation on flight dynamics.These studies mainly analyzed the stability of flexible missiles without vibration control.

A flexible missile undergoes elastic vibration disturbed by aerodynamic force, inertia force, elastic force and follower thrust.Elastic vibration brings additional deformation of the structure,which is the feedback signal to the closed loop, resulting in an aeroservoelastic problem.The aeroservoelastic problem has a great influence on the stability of the flexible missile. The effective suppression of structural vibration becomes vital for the stability of flexible missiles.Vibration reduction control of flexible missiles has attracted the attention of many scholars.Passive control and active control are the most popular control strategies to suppress the vibration of flexible missiles. Passive control mainly uses a notch filter [11-15], and the zero point of the filter is used to cancel the high-frequency pole of the control object. The notch filter reduces the influence of elastic vibration on the control system by filtering noise rather than attenuating elastic vibration. Compared with passive control, active control has good adaptability in complex environments. Active control applies a control force, which is generated by a steering gear, vectored nozzle and piezoelectric actuators, to quickly suppress the vibration. Moreover, some advanced control theories, such as robust control [16-18] and variable structure control[19],have been investigated for the active control of elastic missiles.Liu et al.[20]put forward three attitude control schemes based on passive control, active control and compound control.

The dynamic vibration absorber (DVA) is a well-established vibration control device that is extensively utilized for its excellent performance in terms of reliability and low cost to attenuate vibrations in rotor systems[21-25],propulsion shaft systems[26,27],and railway vehicles [28-30] and for suppressing aircraft flutter[31-33]. Ring-type absorbers are widely used for vibration suppression of rotor systems [21-23]. To optimize the parameters of the DVA, the simulated annealing algorithm combined with the particle swarm optimization algorithm [34], H∞and H2optimization[35],and fixed-points theory[36,37]have been proposed.The passive absorber works over a very narrow frequency and becomes inefficient as the frequency shifts; thus, the active dynamic vibration absorber (ADVA)was developed and introduced. The ADVA is achieved using external actuator forces to suppress vibration.Although the ADVA has been researched and applied in many industrial fields,there are no contributions in the literature focusing on the ADVA-based vibration suppression technique for flexible missiles.

This paper focuses on the active vibration control of a flexible missile using ADVA methodology. Considering the effects of spin and thrust, the equations of motion of a missile with an ADVA are derived based on the Lagrangian approach.A ring-type ADVA based on proportional-integral-derivative (PID) control is designed to suppress the inevitable vibration of the missile.With the minimum root mean square(RMS)of the lateral displacement response of the center of mass taken as an objective function, a GA is used to optimize the parameters of the DVA and PID controller. The vibration response of the flexible missile with an ADVA is analyzed through numerical calculations.

2. Coordinate systems

In this study,the general motion of a flexible missile is described with three kinds of coordinate system: an earth-fixed coordinate system Axyz, a body-fixed coordinate system Ox1y1z1, and a thin disk coordinate system O′ξηζ, as shown in Fig.1.

The earth-fixed coordinate system Axyz is the inertia coordinate system.The body-fixed coordinate system Ox1y1z1is defined under mean axis conditions, where point O is instantaneous center of mass of missile; as shown in Fig. 2, ϑ and ψ are the pitching angle and yaw angle, respectively. The transformation matrix Lϑψ from earth-fixed coordinate system to body-fixed coordinate system is

The coordinate system O′ξηζ is fixed to the thin disk, and the origin of coordinate O′is located in the center section of the thin disk. System rotation around the third axis and second axis is measured as θzand θη′, respectively, as shown in Fig. 3. The transformation matrix Lθη′θzfrom the body-fixed coordinate system to a thin disk coordinate system is

3. Equations of motion

As shown in Fig.1,the relationship between the position vectors is TVector is italic

Fig.1. Coordinate systems of flexible missile.

Fig. 3. Transformation from body-fixed coordinate system to disk coordinate system.

where r and r0are the position vector of the thin disk and the missile center of mass in the earth-fixed coordinate system,respectively, and rxand u are the longitudinal position vector and transverse elastic displacement vector of a thin disk in the bodyfixed coordinate system, respectively. In addition, ω0is the rotation angular velocity of the body-fixed coordinate system relative to the earth-fixed coordinate system. The dot above the vector denotes the relative derivative of the vector with respect to time in the respective coordinate system. The vectors in the body-fixed coordinate system are

3.1. Design of the ADVA

The configuration of the proposed ring-type ADVA is shown in Fig.4.It is composed of a connection unit,mass unit,stiffness unit and damping unit. The connection unit is the outer ring, which is sheathed on the inner ring of the missile. Vibration and force are imposed on the missile body through the outer ring.There are eight identical sets of springs and dampers in the stiffness and damping units, respectively. Space in the inner ring is available for onboard devices.The finite element model of the flexible missile with ADVA is shown in Fig.5,where m0is the ring mass and k0and c0are the stiffness and damping of the ADVA, respectively. In the figure, the proposed ring-type ADVA is placed at the ith node. Here, uy0and uz0are the vibration displacements,Fz0is the control force,xmis the axial position of the ADVA from the tail of the missile,and d1and d2are the outer diameter and inner diameter,respectively,with d1=300 mm and d2= 290 mm. Finally, N =76 is the number of elements.

Fig. 4. Schematic of the active dynamic vibration absorber.

3.2. Kinetic energy, elastic potential energy and dissipative energy

The kinetic energy of the missile and vibration absorber consists of translational kinetic energy and rotational kinetic energy.

where lbis the length of the missile; ω=ω0+ωbis the absolute angular velocity, where ωbis the rotation angular velocity of the thin disk coordinate system relative to the body-fixed coordinate system.In addition,djbis the inertia tensor of the thin disk,and the matrix of djbin the thin disk coordinate system is denoted as

where I is the moment of inertia of the cross section of the thin disk and ρ is the material density. Furthermore, ω0and ωbin the thin disk coordinate system are

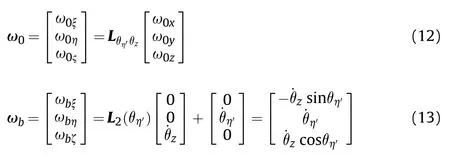
Fig. 5. Finite element model of the missile and active dynamic vibration absorber.

According to the mean axis conditions [6], the kinetic energies of the missile and vibration absorber are written as

where A is the cross-sectional area andis the missile mass. In addition,θzand θy(θη′≈θy) are the elastic rotations of the thin disk.

The elastic deformations of the missile in terms of mode functions and generalized coordinates are as follows.

where φi（x） and Φ are the ith displacement mode shape and displacement shape matrix,respectively.Assuming that the missile is symmetric, the ith displacement mode shape in the y and z directions is equal to φi（x）. In addition, η1i（t） and η2i（t） are the corresponding generalized coordinates,and η1and η2are generalized coordinate vectors.

In contrast to the Euler-Bernoulli beam model typically used in missile modeling, the Timoshenko beam takes into account the shear effect and rotary inertia.When the slenderness ratio is small,the Timoshenko model can be used[38].In the Timoshenko beam model, the rotation angle is expressed as

where Ψ is the rotation angle shape matrix.

Substituting Eqs.(15)and(16)into Eq.(14),the kinetic energy is written as

where

The elastic potential energy of a missile and vibration absorber is expressed as

where EI and κGA are the bending stiffness and shear stiffness,respectively. In addition,, and

The dissipative energy of the missile structure and vibration absorber is written as

where c1and c2are damping coefficients. The damping matrix is

Here,CDin terms of proportional damping is expressed as

where ωiis the ith natural frequency, μirepresents the bending modal damping,and Miiis a diagonal element of the mass matrix M.

3.3. Aerodynamic forces and moments

Using quasisteady theory of the slender beam,the local effective angle of attack α and angle of sideslip β [39,40] are expressed as

where α0and β0are the angle of attack and sideslip of the rigid missile, respectively, andandare the bending slopes.

Here, fy（x，t） and fz（x，t） are the aerodynamic load distributions on the vehicle in the y and z directions, respectively.

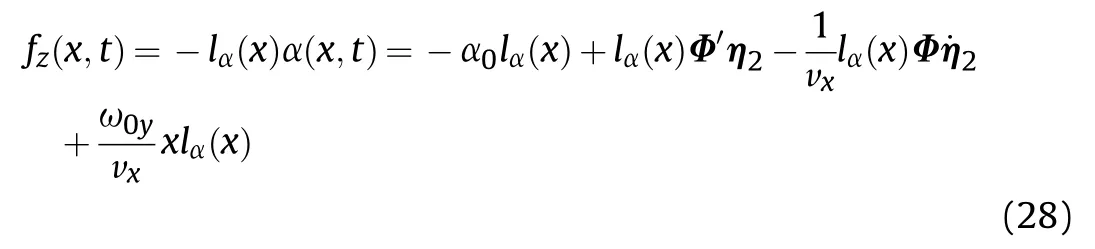
where lα（x）and lβ（x）are the lift and side force derivatives per unit length,respectively, and lα（x） = lβ（x）.

The aerodynamic forces are written as

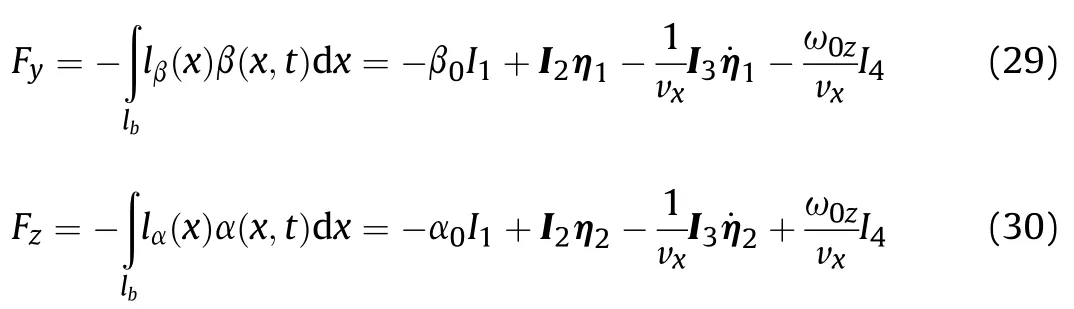
The virtual work δW due to virtual displacements δη1and δη2is written as

where the generalized forces are

The aerodynamic moments are expressed as

where the coefficients Iiare defined in Appendix A.

The work of the axial thrust [6] is

where PNis the axial force.

The virtual work of the thrust is

where xPis the axial position of the thrust application point.Here,δuy（xP，t） and δuz（xP，t） are the virtual displacements at the thrust application point,

The virtual work of the control force of the vibration absorber is

where Fy0is the control force in the y direction. In addition, δuy0and δuz0are the virtual displacements of the vibration absorber,andandare the virtual displacements at point xm.

In general, Lagrange’s equation for the generalized coordinates and forces is

Substituting the kinetic energy in Eq. (17), potential energy in Eq.(20),dissipative energy in Eq.(22),the work of the axial thrust in Eq. (36), and the virtual work in Eq. (38) and Eq. (40) into Lagrange’s equation and defining η1and η2as the generalized coordinates,the elastic vibration equations of the missile are found to be

According to Lagrange’s equations in the floating coordinate system [41,42], the angular velocity equations are obtained as

where Mxis the aerodynamic moment of the longitudinal direction of the missile.

The translational equations are expressed as

where Fxis the force in the x direction.

Assuming that vxis taken as a constant, coupling items and higher-order nonlinear terms are ignored. Eqs. (42)-(51)are simplified to obtain the longitudinal equations of motion. The coupled dynamic equations of the rigid body modes and elastic modes can be expressed as

where x1is the axial distance of the ADVA from the center of mass.

Eqs. (52)-(55) can be written in state space form as

where I is the unit matrix;the coefficients of matrix A are defined in Appendix A.

Fig. 6. PID controller for the flexible missile.

4. Design of the PID controller

4.1. PID controller

The PID controller is the most widely used method in vibration control. Gani et al. [43] and Khot et al. [44] researched the active vibration control of a cantilever beam using a PID controller.Rubio et al.[45]designed a PID controller to decrease the vibration effects of a robotic arm,and Metin et al.[46]controlled vertical rail vehicle vibrations using a parameter adaptive PID controller. A schematic diagram of the PID controller for a flexible missile is shown in Fig.6.GA is used to adjust the three coefficients of PID.The PID controller focuses on the minimization of the control error e = r- y, the control output u is converted into the vibration absorber, and the vibration absorber generates a control force to suppress the vibration of the flexible missile. The control output u is

where kpis the proportional gain,kiis the derivative gain,and kdis the integral gain.

4.2. Objective function

PID tuning is a difficult problem, even though there are only three parameters. GAs [47-49] have been widely used in PID tuning.The RMS of the lateral displacement response of the vehicle is taken as the objective function, whose smallest value serves as a reference for the fittest individuals in the minimization problem.The objective function can be expressed as

where n is the number of time steps and uz（x，tj） is the lateral displacement response of the missile in the jth time step. The fitness function of the GA is the same as the objective function.

5. Numerical examples

To verify the validity of the ADVA,a flexible missile is analyzed.In this section,the parameter of the flexible missile with a fineness ratio of 25 is given as Table 1 and Figs.7-9,λBis the fineness ratio.The first two mode shapes are illustrated in Fig. 10. The lateral aerodynamic coefficient derivative distribution along the longitudinal axis of the missile is shown in Fig.11.

Fig. 7. Mass distribution of the missile along the longitudinal axis.

Fig. 8. Rotational inertia distribution of the missile along the longitudinal axis.

Fig. 9. Stiffness distribution of the missile along the longitudinal axis.

5.1. Simulation of the ADVA without follower thrust

The parameters of the DVA and PID controller are obtained by the GA.The parameter settings of the GA are as follows:population size: 100, crossover rate: 0.4, mutation: 0.01, and generation number: 100. The range of the initial population is xm∈[1，76]，xm∈N, m0∈[0.1， 10], c0∈[0.1， 400], and k0∈[0.1， 4 × 104]. The optimized parameters of the DVA are xm=76,m0=9.9,c0=399,and k0= 36394. The best position of the DVA is the nose.

With these fixed DVA parameters, the PID parameters are optimized by the GA.The PID parameter range is kp，ki，kd∈[0，3000],and the optimum values of the PID parameters are kp=2818,ki=2476, and kd= 2999.

Under three different conditions, namely, without control (no DVA), with passive control (DVA) and with active control (ADVA),the dynamic response without follower thrust is analyzed. The numerical results are shown in Figs. 12-14 and Table 2. The amplitude of the pitch and attack angle with the ADVA decreases gradually;when the settling time is 2 s,the DVA has little effect on the pitch and attack angle, as shown in Fig. 12. The lateral displacement amplitude of the center of mass with the DVA and ADVA is smaller than that of no DVA in Fig.13(a). The ADVA and DVA are effective in suppressing the vibration by approximately 41.2% and 17.6%, respectively, compared with no DVA as shown in Table 2; although the maximum amplitude of the ring position is increased, the settle time is shortened as shown in Fig. 13(b).Compared with the other two configurations, the lateral displacement with the ADVA is the smallest,as shown in Fig.14.

5.2. Simulation of the ADVA with follower thrust

The flexible missile in the active stage is affected by follower thrust, which causes axial compression of the body structure, reduces the stiffness of the structure, and changes the vibration characteristics of the system. Therefore, it is necessary to analyze the influence of follower thrust on the vibration characteristics of the flexible missile.

When the follower thrust is 6×105N,the numerical results are as shown in Figs.15-17 and Table 2.The amplitude of the pitch and attack angle become larger, the settle time becomes longer as shown in Fig. 15, and the lateral displacement amplitude of the center of mass increases as shown in Fig. 16(a). The effect of follower thrust on the elastic vibration is substantial. The ADVA and DVA are effective,suppressing the vibration by approximately 47.6%and 23.8%,respectively,compared with no DVA as shown in Table 2,and the effect of vibration reduction is more effective than that without follower thrust. The amplitude of the ring position increases under thrust as shown in Fig. 16(b) and Table 2. Fig. 17 depicts the change in the control force under different follower thrusts; as the thrust increases, the control force gradually decreases.

Fig.10. The first two mode shapes of the missile.

Fig.11. Lateral aerodynamic coefficient derivative distribution along the longitudinal axis of the missile.

Table 2 The RMS of lateral displacement under different working conditions.

6. Conclusions

This paper investigates the feasibility of using an ADVA for active vibration control of a flexible missile system through simulation. A ring-type ADVA based on PID control is first designed to suppress the otherwise inevitable vibration of the missile. The motion equations of the flexible missile with the ADVA are derived based on the Lagrangian approach. DVA and PID controller parameters are obtained by a GA.According to the comparison of the numerical simulation results of the flexible missile, the following conclusions can be drawn:

1) The DVA is effective in suppressing the vibration,and the ADVA performs better than the DVA.

Fig.12. Displacement response of the missile at P = 0N.

Fig.13. Displacement response of the missile at P = 0N.

Fig.14. Lateral displacement along the longitudinal axis of the missile at t = 4s.

Fig.15. Displacement response of the missile at P = 6× 105N.

Fig.16. Displacement response of the missile at P = 6× 105N.

Fig.17. Control force under different thrusts.

2) Following thrust exacerbates the elastic vibrations; the amplitude of the pitch and attack angle with follower thrust become larger, the settle time becomes longer, and the vibration reduction effect of the ADVA and DVA is more effective than that without follower thrust.

3) As the follower thrust increases, the control force gradually decreases.

Funding

This work was supported by the National Natural Science Foundation of China (10972033).

Declaration of competing interest

The authors declare that there is no conflict of interests regarding the publication of this paper.

Acknowledgments

This work was supported by the National Natural Science Foundation of China.

Appendix A

1. The aerodynamic coefficients and integral coefficients are

2. Coefficients of matrix A