基于仿射变换的微型无人机编队飞行控制技术

杨庆凯 潘云龙 周勃 刘虹 方浩

1．北京理工大学自动化学院北京100081

近年来,随着各国军事力量的不断增强,传统打击武器已经很难满足作战需求.为完成更加复杂的作战任务,多平台协同编队成为越来越重要的协作方式.

现代战争中的陆用运动体以多系统协同为主要作战模式,陈杰等将编队控制作为多系统协同指挥控制中重要的研究方向之一[1].在文献[2] 中,徐世均等采用作战决策建模技术对编队作战指挥过程进行量化建模,不仅保证作战效果最优化,而且该模型具有较好的弹性和较广的适用范围,建立了一种适用于各级海上编队的作战决策模型.在航空作战任务中,刚建勋等根据实际作战任务对航母编队进行了能力需求分析,为航母编队的集成配置、能力需求论证提供方法指导[3].针对美国近年来对有人/无人协同作战在军事方面的重视,申超等分析了有人/无人协同作战中分散编队的动态、适应性任务规划等技术,为相关领域军事发展提供了参考情报[4].

多智能体编队控制的目标一般是指在控制策略的作用下,智能体间通过交互形成期望的队形.经过多年的研究,已经形成了多种控制体系结构.最近Ahn 教授在文献[5]中对已有研究进行了梳理,指出大部分编队控制算法可划分为基于绝对位置、相对位置和距离3 种类型.其中虽然基于绝对位置的方法简单易实施,但是却强依赖于全局定位系统[6].基于相对位置的方法对图的连通性要求较宽松,但是局部坐标系朝向需保持一致[7].近期,编队控制又产生了一系列新的成果.Eren 在文献[8]中较早地讨论了基于方位(bearing)的编队控制问题,并为轮式移动机器人设计了相应控制策略.赵世钰等在文献[9]中研究了方位角约束下的队形唯一性问题,并设计了基于方位角的编队控制律,证明了系统的全局收敛性.针对环形队形,王晨等在文献[10]中设计了基于极限环的控制算法,将编队任务分解为包围和队形生成.谢广明等将事件驱动的强化学习方法用于解决编队控制问题[11].

随着编队控制研究的深入,为了更好地适应复杂环境及动态任务,许多学者将研究重心转移到了编队变换控制.Coogan 等通过构造一种称为“监控图”的拓扑,分别基于单边和多边交互提出了队形伸缩控制算法[12].赵世钰等还利用智能体间的方位角实现了队形的平移和伸缩变换,证明了变换系统的全局稳定性[13].除了上述研究,还有一大类研究利用仿射变换的思想研究编队变换问题.在文献[14]中,Rastgoftar 等将队形变换问题建模为齐次形变,借助于物理学中的连续介质力学理论设计了编队控制器.林志赟等就仿射队形可镇定的拓扑条件给出了严格的理论分析,证明了无向图下仿射控制问题可解决的充要条件是该无向图是普遍刚性的[15].在此基础上,赵世钰在文献[16] 中首先给出了仿射定位中的领航者选择条件,然后分别针对领航者速度常值和时变情形,设计了仿射编队变换控制器.

分布式定位作为分布式协同控制的基本保障,与编队控制密不可分.现有的分布式定位算法根据测量变量,大致可分为基于距离、方位角和相对位置的定位.在基于距离的定位方法中,柴国飞等考虑了时变拓扑下的定位问题,在一致性估计和持续激励条件下,解决了单特征点动态定位问题[17].Shames等在文献[18]中考虑了带有测量噪声情况下的角度可定位条件.在文献[19]中,Oh 和Ahn 等利用一致性理论,结合相对距离和方位角测量信息,解决了定位和编队控制问题.林志赟等在文献[20] 中也考虑了混合测量信息下的分布式定位问题,通过建立与质心坐标相关的一致线性方程,设计了一类迭代定位算法.不久前,韩志敏等在复拉普拉斯框架下设计了仅基于相对位置和速度信息的定位编队联合算法,有效融合了定位和编队任务[21].

我们团队近年来对基于仿射变换的编队控制进行了深入的研究.在文献[22]中,笔者给出了基本的普遍刚性图的构建方法,并针对一阶积分器系统引入了基本的仿射队形控制器.在文献[23]中,笔者讨论了队形伸缩控制,解决了当群体中只有两个智能体知悉期望队形信息下的编队控制问题.进一步在文献[24] 中,攻克了队形信息隐含于某一条边中的情形,提出了一类分布式估计器,精确地估计了队形伸缩因子,在此基础上完成了控制器的设计.笔者还在文献[25] 中探讨了应用仿射队形控制,智能体交互图需满足的条件以及该类拓扑的设计方法,并将其应用于编队控制中.

1 理论基础

无人机间的通信/交互关系用无向图来描述.集合v= {1,2,···,n} 和集合ε ⊆v×v分别表示无向图g中的点集合和边的集合.当且仅当点i和点j是彼此的邻居时,图g存在一条边(i,j).与点i相邻的点集合由Ni= {j|(i,j)∈ε} 表示.将一个无向图嵌入到欧式空间中,该图便有了相应的位形,由q= [qT1,···,qTn]T表示.如果q中的坐标在有理数范畴内是代数无关的,则称位形q是一般的(generic).由图g和该位形q组成的二元组构成了一个结构(g,q).

一般结构的刚性可以用应力矩阵来表征.将标量ωij赋值给结构(g,q)中的边(i,j),并且用向量ω = (···,ωi j,···)T∈Rm表示边应力的集合.当ω 满足下式时

称ω 为结构(g,q)的一个平衡应力系数.式(1)写成紧凑形式为

其中,Ω ∈Rn×n为应力矩阵,定义为

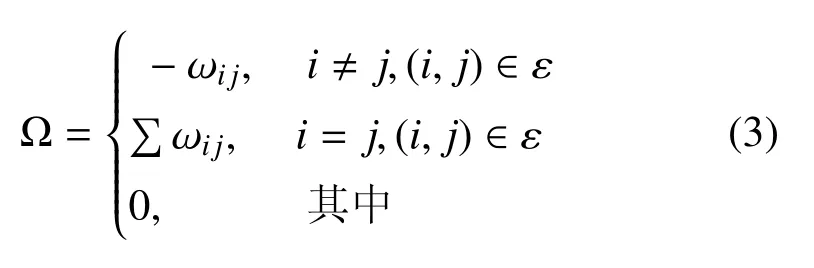
在一般位形下,当应力矩阵Ω 的秩为n−d−1且Ω 半正定时,则结构(g,q)是普遍刚性的.

接下来,在这里介绍关于位形q的仿射变换,定义为

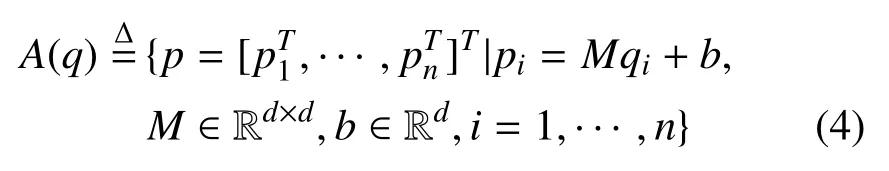
或等价写成

其中,实矩阵M表示旋转和伸缩变换,b表示平移变换.结合式(1)和式(4)可得

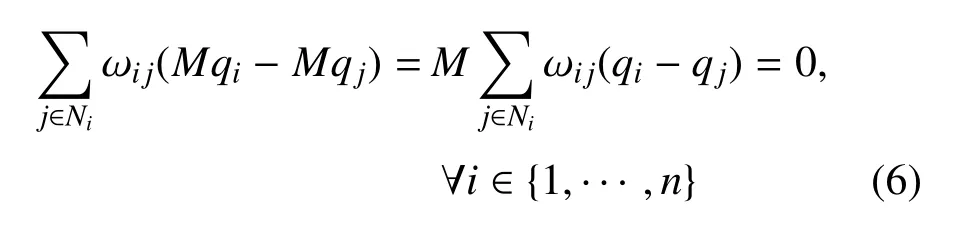
易知,在仿射空间中,平衡应力不会随着队形的伸缩、旋转或者平移发生改变.

2 硬件平台搭建

2.1 无人机

Crazyflie 2.0 是一款微型的四旋翼无人机(如图1),斜对角的电机间的距离为92 mm,带电池情况下的重量为27 g,适用于室内以及集群飞行验证.Crazyflie 2.0 采用了STM32F405RG 和NRF51822 两款微控制单元.STM32F405RG 内核为Cortex-M4,主频168 MHz,主要负责对传感器数据的采集与处理,控制无人机的飞行姿态以及驱动4 个电机的旋转.NRF51822 内核为Cortex-M0,主频32 MHz,主要负责无人机与地面站之间的通信,管理电源和加载启动任务等辅助功能.该芯片支持蓝牙、2.4 GHz 无线通信方式,能够实现无人机与手机、电脑等设备间的通信.Crazyflie 2.0 装有MPU9250 和LPS25H 两款传感器,能够有效保证无人机飞行过程中的稳定性.MPU9250 内部集成有3 轴陀螺仪、3 轴加速度计和3 轴磁力计,用于对无人机角速度、加速度以及偏航角的测量.LPS25H 是一款气压传感器,可以有效防止螺旋桨在旋转过程中引起气流变化而引起的气压变化.Crazyflie 2.0 上标准电池容量为170 mAh,有效飞行时间为7 min.

图1 Crazyflie 2.0 微型无人机

2.2 动作捕捉系统

由于无人机本身重量较轻,处理器的性能也较弱,无法安装GPS 或摄像头来实现自身的定位.MOTION ANALYSIS 动作捕捉系统由一组若干个动作捕捉摄像头(如图2)、动作捕捉软件Cortex(如图3)以及动作捕捉附件组成,有着非常优秀的性能,可以在室内实现毫米级精度的定位.通过给无人机贴上光学反光球型标记点,可以使用MOTION ANALYSIS 动作捕捉系统来间接追踪无人机的位置.另外,需要一台电脑安装配套的动作捕捉软件Cortex 来获取球型标记点的位置.官方推荐的电脑配置为4 核3.2 GHz CPU,8 GB 内存,Windows 7 (64 位)操作系统,显存容量256 MB.

2.3 地面站

地面站上装有Crazyradio PA,Crazyradio PA 是一个2.4 GHz 的USB 无线电适配器,能够传输32 个字节的数据包,传输速率高达2 Mbit.通过该无线电适配器,地面站能够获取无人机的状态、信号强度以及机载传感器的数据,并向无人机发送控制指令以完成各种复杂的飞行任务.地面站上装有ROS Kinetic 机器人操作系统,用于实现对无人机的控制.ROS 支持C++ 和Python 等多种编程语言,我们的控制代码均在该框架下运行.另外为了获取无人机的位置信息,地面站还需要与安装Cortex 软件的电脑处于同一IP 地址下,借由官方提供的SDK,通过TCP/IP 通信协议获取动作捕捉系统的数据.硬件结构框图如图4所示.

图2 Motion Analysis 动作捕捉系统摄像头

图3 Cortex 软件界面

3 实物实验

3.1 控制算法

基于仿射变换的思想,采用的无人机控制算法如下[26].

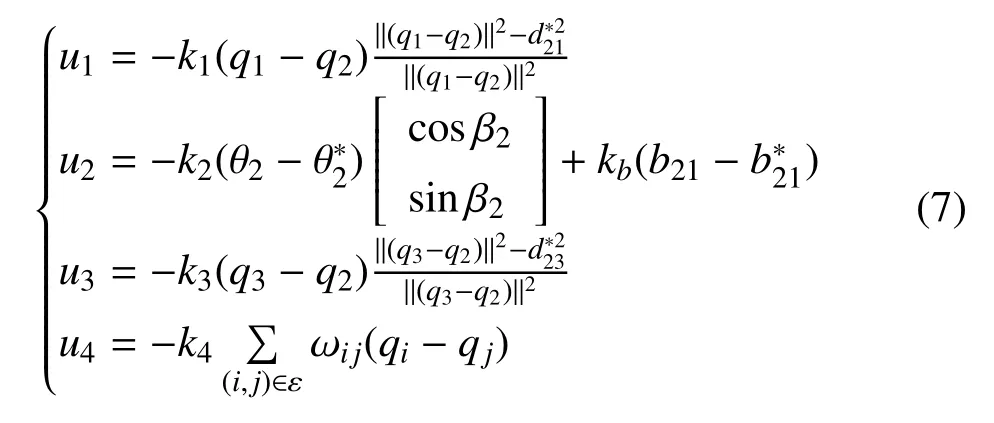
其中,ki＞0 表示常数,θ2和θ2∗分别表示2 号无人机与1、3 号无人机之间的实际和期望的夹角,b21和分别表示2 号无人机指向1 号无人机的实际和期望的朝向,d∗21表示2 号无人机与1 号无人机期望的距离,d∗23表示2 号无人机与3 号无人机期望的距离,ωi j的设计需要满足式(1).一些符号的含义示意图如图5所示.

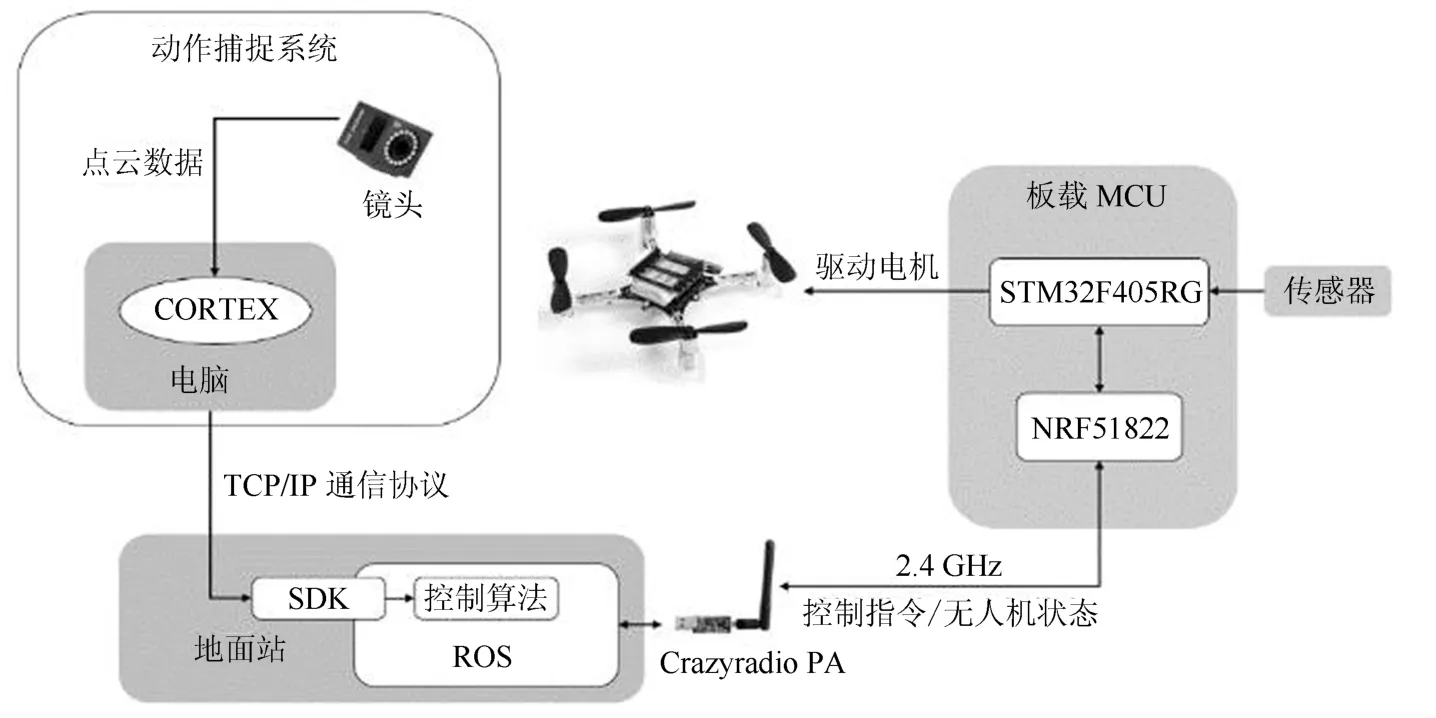
图4 硬件结构框图

图5 编队示意图

从控制律中可以看出,仅仅1 号、2 号和3 号无人机需要知道跟期望的队形相关的信息.1 号和3 号无人机跟2 号无人机保持期望的距离,2 号无人机负责控制期望的角度和朝向.

3.2 实验结果

在实物实验中,如图6所示,首先利用控制律实现4 台无人机的编队,形成期望的正方形标称队形.

图6 无人机的标称队形

再改变无人机间期望的距离、夹角和朝向,实现队形的伸缩、旋转等变换.队形的变换过程如图7所示,无人机的队形依次经过拉伸、旋转、再旋转回原位,切变的变换过程.

图7 无人机的队形变换

4 结论

本文研究了混合控制变量下的分布式编队控制问题,其中两个是距离量,一个是角度量.在考虑具有不同传感器的异构智能体的情况下,这样的控制设置很有意义.通过使用应力矩阵来利用仿射编队控制技术,可以通过控制3 个无人机来稳定和灵活地改变编队形状.实现“以少控多”.此外,整个编队的方向可以通过向仅配备有角度传感器的一个无人机加入额外的、基于方位的控制项来控制.实验结果表明了该实物验证平台和控制算法的有效性.下一步主要工作:1)进一步减少算法中的外部信息输入,扩大算法适用范围.2)实现更大规模无人机的编队实物验证.