冰载荷冲击下的推进轴系扭振特性影响分析
2020-07-02武兴伟
武兴伟
(1.上海交通大学 船舶海洋与建筑工程学院 上海200240;2.中国船舶及海洋工程设计研究院 上海200011)
引 言
随着北极地区冰川逐年融化,各国都渐渐意识到北极航线的重要性,在北极地区从事商业运输和科考研究的船只也越来越多。由于北极地区冰川和浮冰带的存在使其不同于其他水域,在此水域航行的船只都面临冰载荷冲击的考验,冰载荷冲击会明显增加船舶推进轴系的扭转振动,使推进轴系各部件的工作条件恶化,这就对推进轴系重要部件的安全可靠性提出了更高要求。
由于冰载荷冲击的存在,推进轴系的瞬时动态扭振响应是需要关注的重点,不同于以往的稳态研究,需要采用时域方法对轴系扭振进行求解计算。国内外对于冰载荷冲击下的轴系扭振问题研究还较少,杨红军[1]对冰载荷冲击下的推进轴系瞬态扭振特性进行了仿真计算,通过与实船测试结果对比,验证了仿真的合理性与可行性。吴帅[2]采用Abaqus分析软件,对冰载荷下柴油机推进轴系扭振进行了计算,并对时频域计算方法进行了对比。廖鹏飞[3]在计算冰载荷下推进轴系扭振时,考虑了冰载荷初始相位角等影响因素。肖能齐[4]对冰载荷下电力推进轴系扭振问题进行了研究,发现冰载荷激励力相较于电机阶次力对轴系扭振的影响要更大。
本文针对某破冰船电力推进轴系,采用时域法中的Newmark-β法对冰载荷下的破冰船推进轴系瞬态扭振特性进行计算,考虑冰载荷冲击初始相位角对轴系扭振的影响;并探究了轴系扭振特性对轴系结构参数变化的敏感性。
1 轴系扭振时域计算方法
1.1 集总参数模型
为进行推进轴系瞬态扭振计算,将实际的破冰船推进轴系简化为12个惯量的集总参数模型,包括电机、联轴器、离合器和螺旋桨等部件,模型如图1所示。
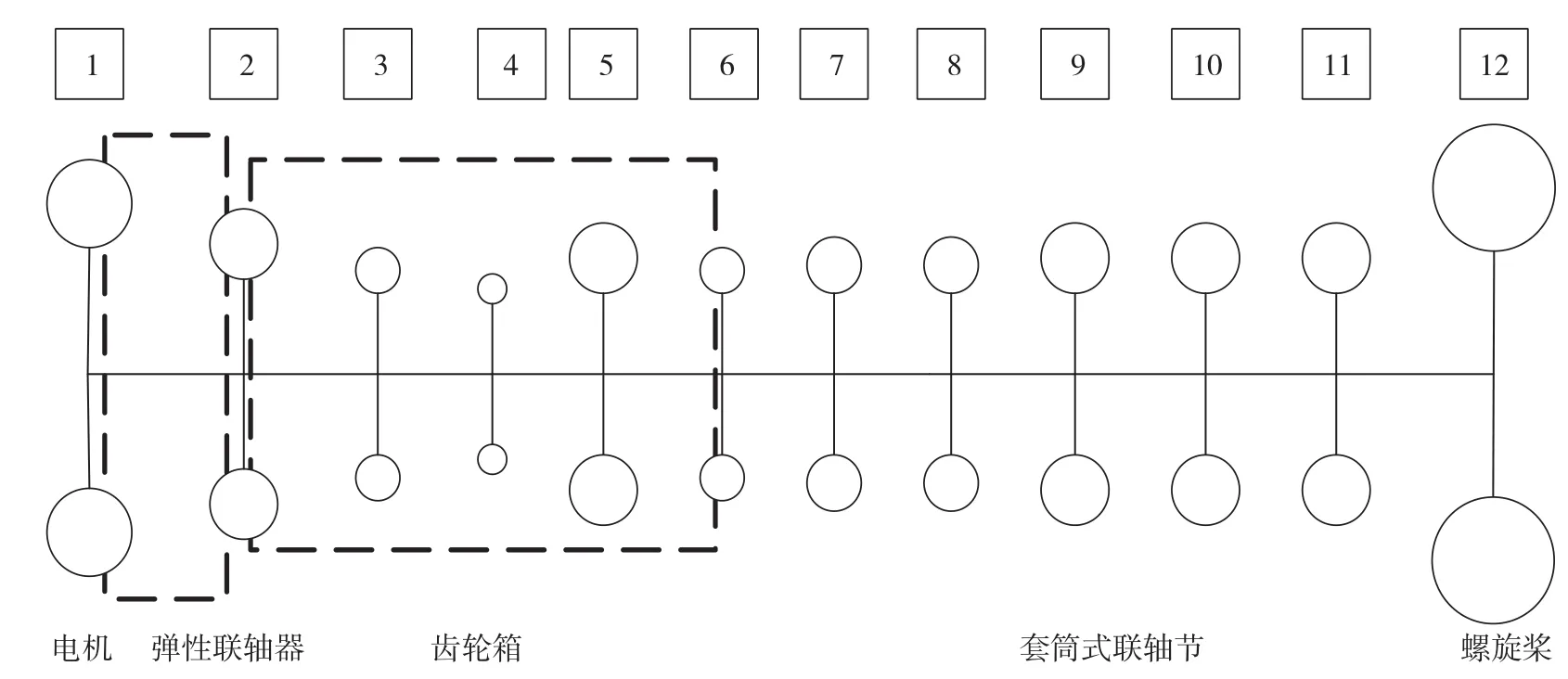
图1 集总参数模型
1.2 激励的形成
本文形成的激励有螺旋桨正常激励和冰区加强条件下不同工况时的冰载荷激励。
1.2.1 螺旋桨正常激励
通常对于轴系装置来说,螺旋桨激励力矩较小,只需考虑其叶频和倍叶频的激励。
经验公式合成:
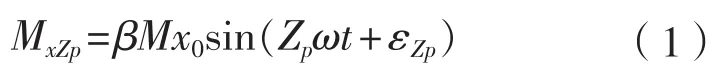
式中:MxZP为螺旋桨平均扭矩,N·m;εZp初相角,(°);β为螺旋桨激振力系数,偶数叶桨β= 0.15~0.2,偶数页桨β= 0.03~0.07。
本文所研究的破冰船螺旋桨为4叶桨,额定功率7 000 kW,额定转速为210 r/min。形成的总螺旋桨激振力矩如下页图2所示。
1.2.2 冰载荷激励
螺旋桨冰载荷是指螺旋桨和冰块相互作用过程中产生的冰撞击载荷。
各船级社规范对冰载荷模型的限定是:螺旋桨的冰载荷不包含冰从侧向(径向)进入已转向的推进器的螺旋桨而产生的螺旋桨和冰相互作用载荷,也不包含冰块冲击牵引式螺旋桨桨毂引起的载荷工况。应对冰冲击推进器本体产生的冰载荷进行估算。
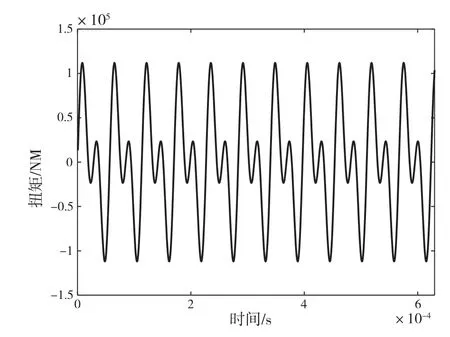
图2 螺旋桨激振力矩
冰区加强条件下最大冰块扭矩定义为:
定距桨和调距桨时:
当D≤Dlimit时,
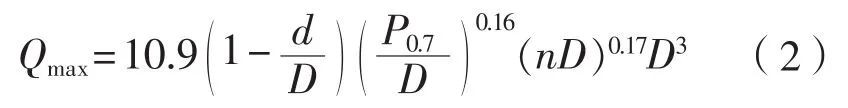
当D>Dlimit时,
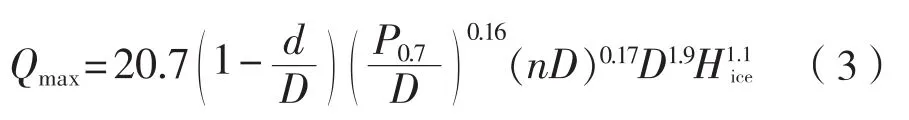
式中:Qmax为最大冰块扭矩,N·m;d为螺旋桨桨毂外径,m;D为螺旋桨直径,m;P0.7为螺旋桨0.7R处的螺距,m;n为螺旋桨转速,r/min;Dlimit为螺旋桨直径的边界值,m;Hice为最大冰块设计厚度,m ;Dlimit=1.8Hice。
导管桨时:
当D≤Dlimit时,
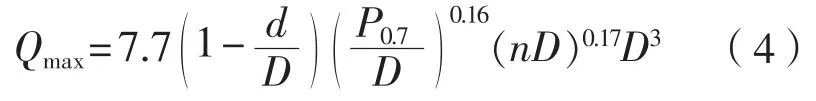
当D>Dlimit时,
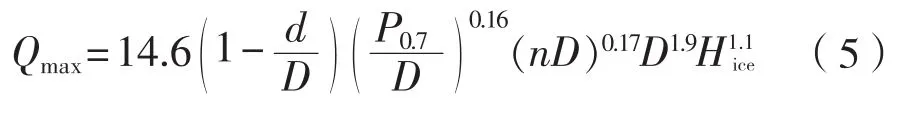
式中 :Dlimit=1.8Hice。
得到最大冰块扭矩后,便可以得到螺旋桨叶片的瞬时扭矩。CCS/FIN/DNV/ABS 对螺旋桨叶片的瞬时扭矩的定义相同,均将作用于叶片上的一系列半正弦波形冲击定义为轴系瞬态扭振分析中的螺旋桨冰块扭矩激励[5-8]。
单个叶片冰块冲击产生的扭矩对应于螺旋桨旋转角速度的函数如下所示:
当φ= 0…αi时,
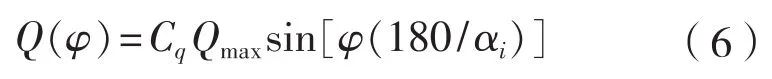
当φ=αi…360 时,

式中:Cq为扭矩作用系数;αi为冰载荷持续作用在螺旋桨上时间(以°计量)。
大量研究证明配戴角膜塑形镜可以显著控制近视增长,并获得良好的日间裸眼视力[2,3],但Chang和Liao[5]对201名小学生的调查发现只有53.2%的儿童日间摘镜后可以获得0.8以上裸眼视力。随着近视患病率的逐年升高,配戴角膜塑形镜的儿童人数也快速增加[1]。因此,探讨去片视力低下的原因以及对近视的控制作用对于提升验配效果意义重大。本研究通过回顾分析北京同仁医院验光配镜中心验配角膜塑形镜的50名近视青少年儿童,发现验配前球镜度越高,去片后的裸眼视力越差,而裸眼视力差儿童的近视增长同样得到了有效控制。
对于冰载荷的加载方式,一般考虑为:在螺旋桨碾碎冰块的过程中,所产生的附加扭矩为各个叶片扭矩的矢量和。在撞击冰块开始和结束的270°范围内,扭矩按线性增减。
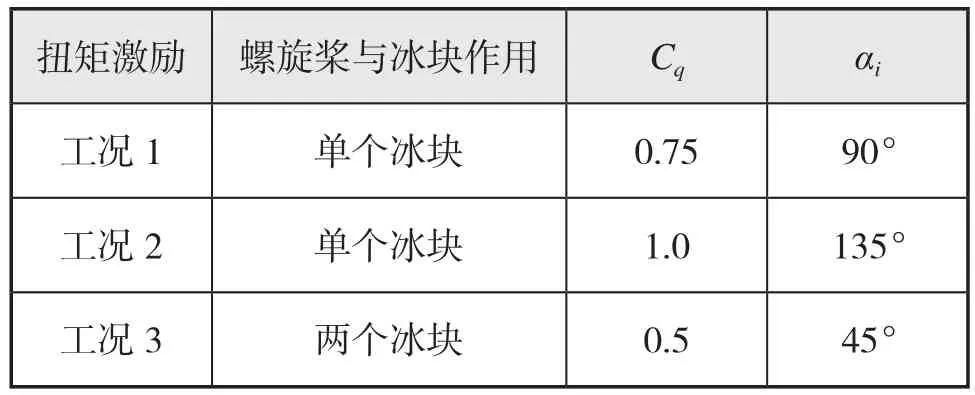
表 1 Cq和 αi值
本文研究的破冰船电力推进轴系螺旋桨直径为4.4 m,破冰厚度为1.5 m,通过上述方法得到的冰区加强条件下3种工况的冰载荷激励如图3 -图5所示。
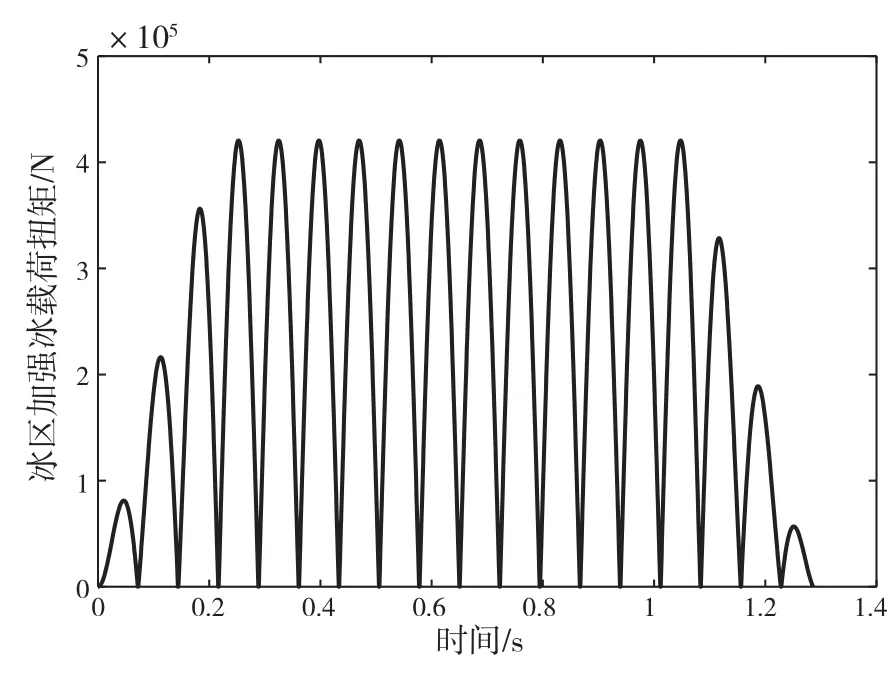
图3 工况1冰载荷激励
1.3 螺旋桨阻尼
螺旋桨阻尼以质量阻尼形式考虑,推荐采用阿尔查(Archer)公式。
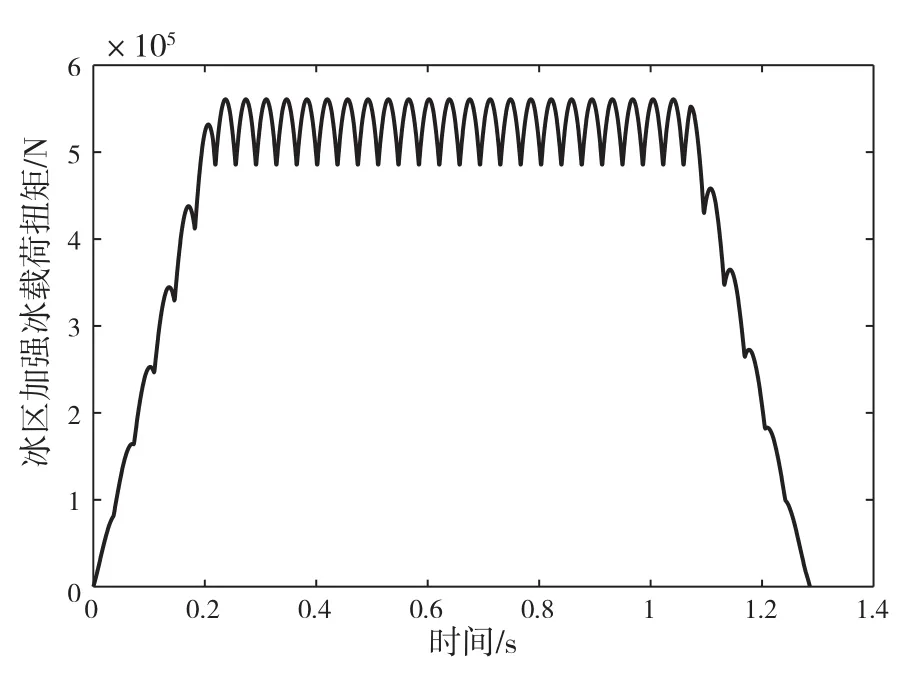
图4 工况2冰载荷激励
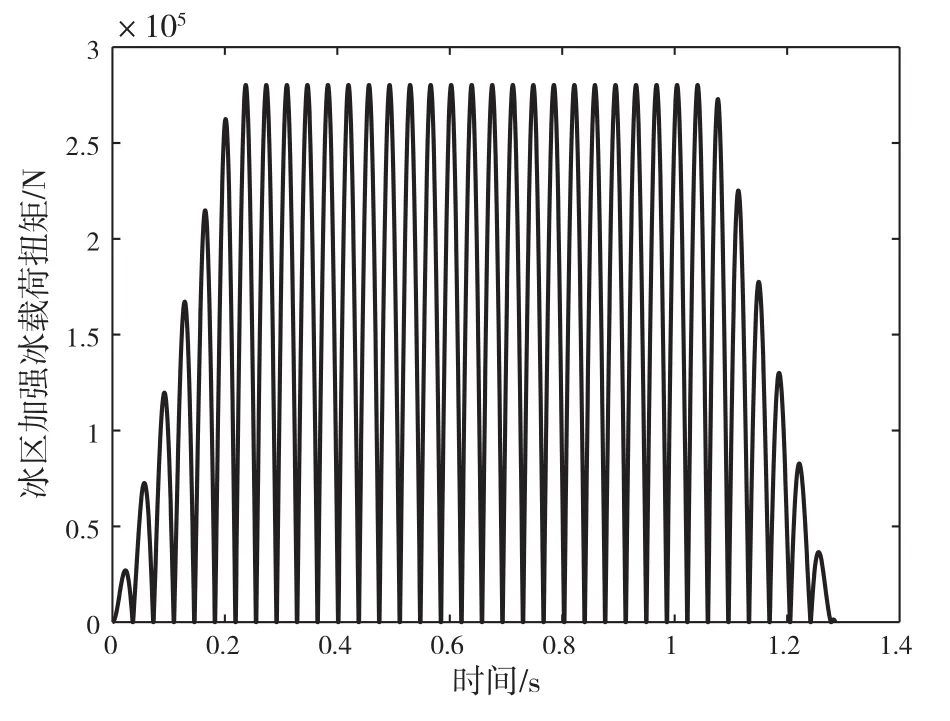
图5 工况3冰载荷激励
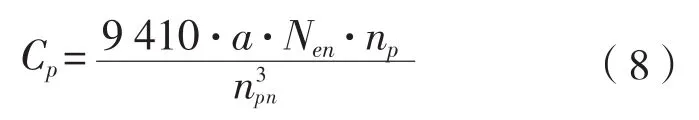
式中:Nen为额定功率,kW;npn为螺旋桨额定转速,r/min;np为计算工况的螺旋桨转速,r/min;a为系数,缺乏螺旋桨资料时,可近似取30。
1.4 Newmark-β 法计算理论
Newmark-β法在解决系统的响应分析中应用较为广泛,因为首先是将时间历程离散化,所以它不仅能解决线性问题,还能很好地解决非线性问题。其系统t+Δt时刻的微分方程为:
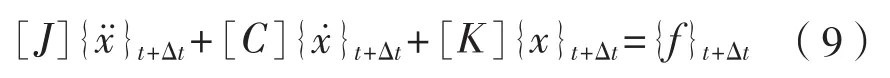
式中:[J]、[C]、[K]和{f}分别为惯量矩阵、阻尼矩阵、刚度矩阵和激励力向量。其具体形式为:
惯量矩阵:
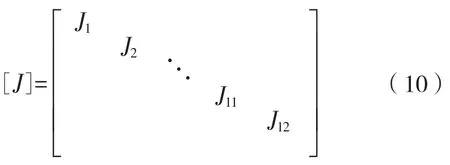
阻尼矩阵:
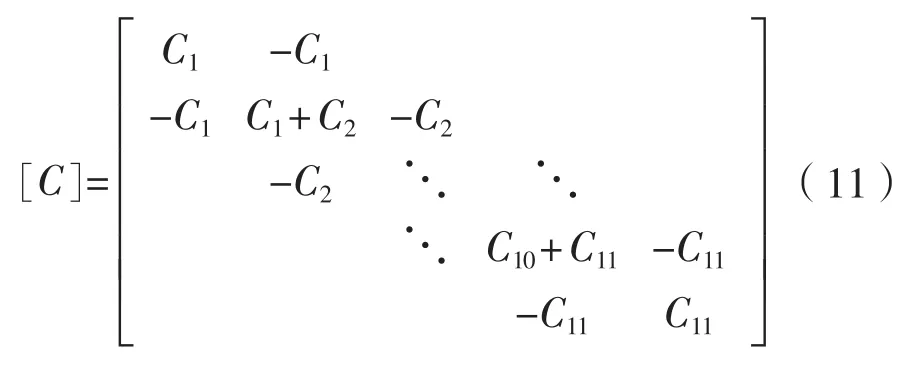
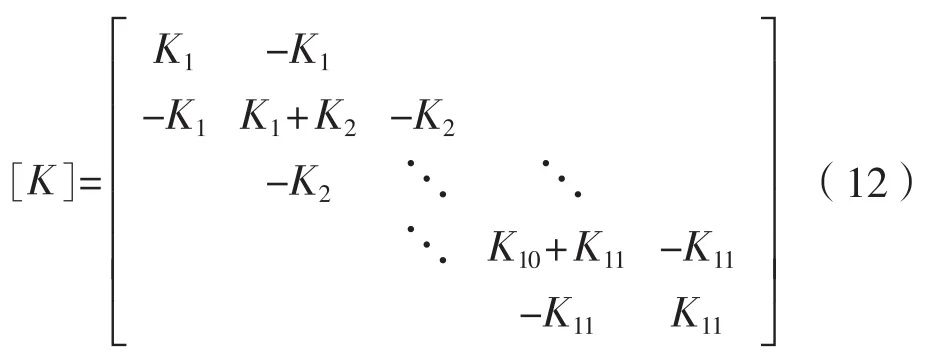
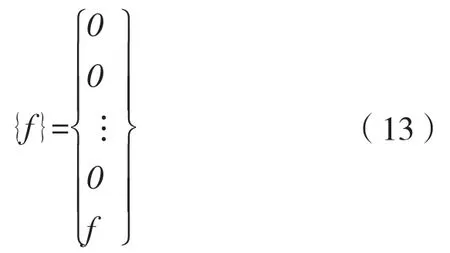
激励力列向量:
Newmark-β法的积分格式为:
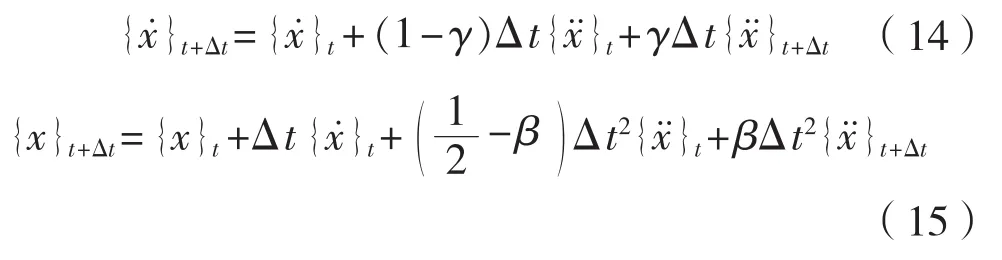
将式(14)和(15)转化得到下式:
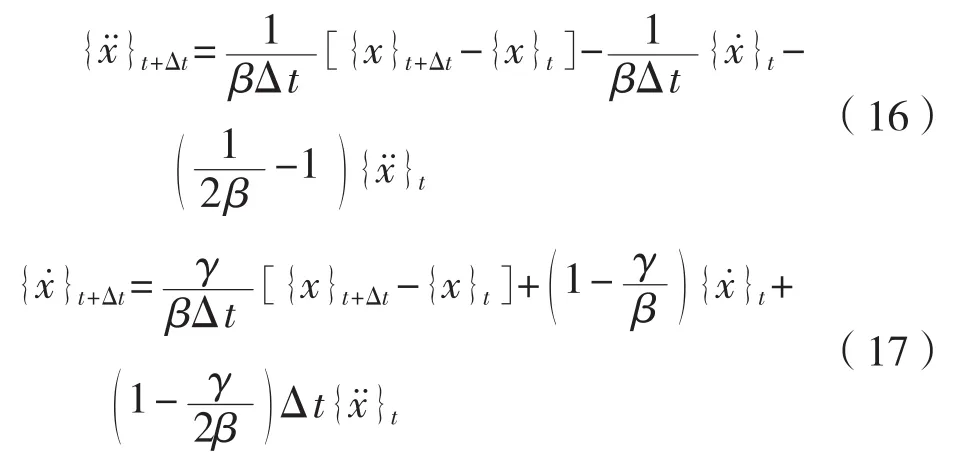
整理得到:
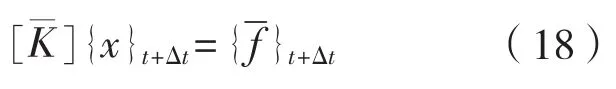
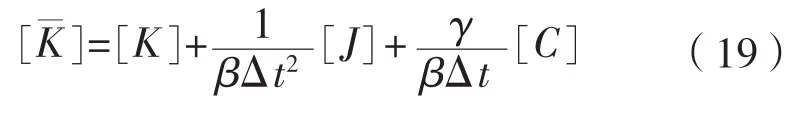
其等效激励力向量为:
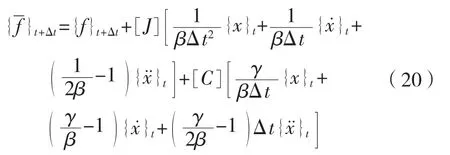
2 推进轴系扭振特性计算
2.1 未考虑冰载荷激励时的结果
计算得到的不存在冰载荷冲击时的推进轴系各轴段附加扭矩和后轴系部分最大附加应力如图6和图7所示。
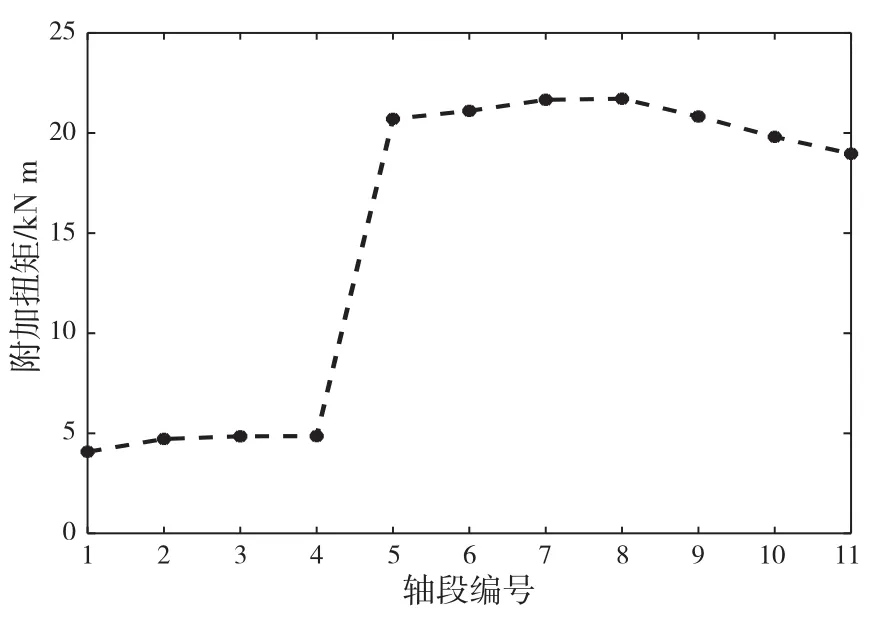
图6 各轴段附加扭矩
从图中可以看出,由于是电机驱动,所以推进轴系各部分的扭矩和应力值都较小。
2.2 考虑冰载荷激励时的结果
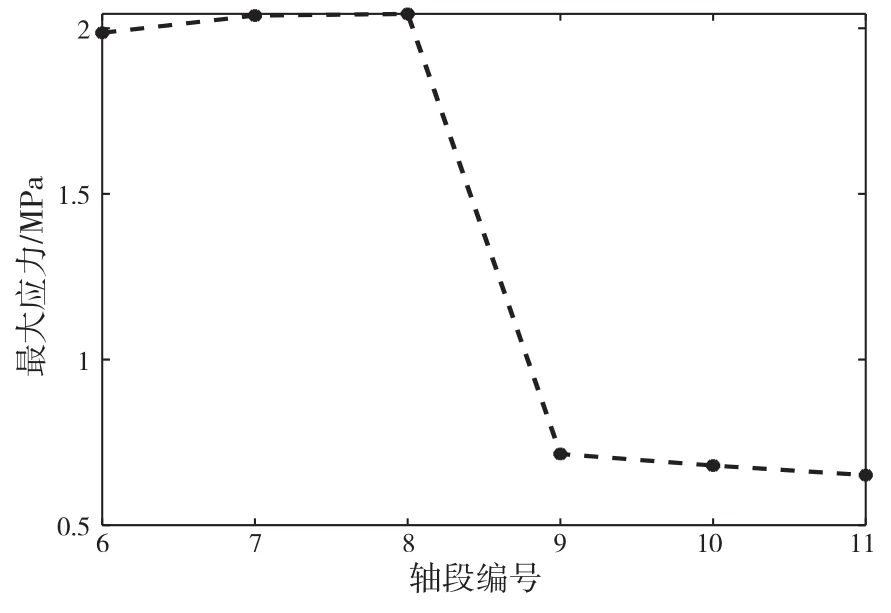
图7 后轴系部分各轴段最大应力
针对冰区加强条件下的3种不同工况,分别对其进行仿真,考虑冰载荷加载的初始相位角对轴系瞬态扭振特性的影响。冰载荷在轴系运行稳定以后开始加载,从0°~360°以每1°为步长,加入冰载荷冲击,找出对推进轴系扭振影响最大的加载位置。
在额定转速条件下,得到3种工况下的弹性联轴器附加扭矩、螺旋桨轴附加扭矩和后轴系部分轴段最大附加应力。具体结果如图8~图10所示。
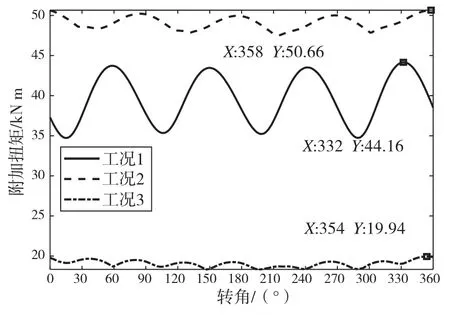
图8 3种工况下弹性联轴器扭矩
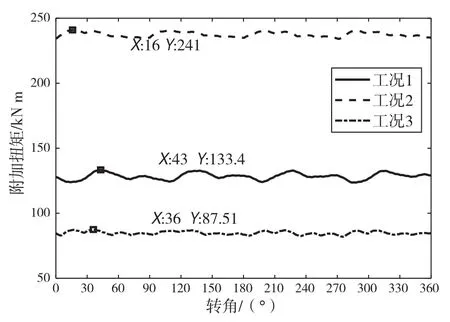
图9 3种工况下螺旋桨轴扭矩
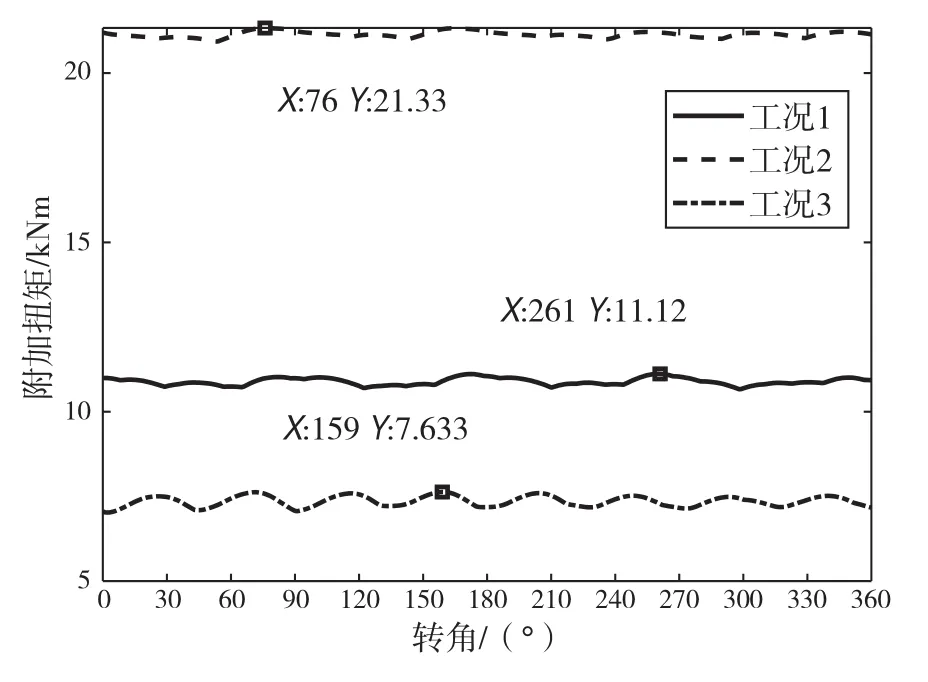
图10 3种工况下后轴系部分轴段最大应力
可以看出,工况1时,在332°加载冰载荷激励,弹性联轴器附加扭矩出现最大值为44.16 kN·m;在43°加载时,螺旋桨扭矩出现最大值为133.4 kN·m;在261°加载时,后轴系部分的几个轴段中出现最大应力,为11.12 MPa。
工况2时,在358°加载冰载荷激励,弹性联轴器附加扭矩出现最大值为50.66 kN·m;在16°加载时,螺旋桨扭矩出现最大值为241 kN·m;在76°加载时,后轴系部分的几个轴段中出现最大应力,为21.33 MPa。
工况3时,在354°加载冰载荷激励,弹性联轴器附加扭矩出现最大值为19.94 kN·m;在36°加载时,螺旋桨扭矩出现最大值为87.51 kN·m;在159°加载时,后轴系部分的几个轴段中出现最大应力,为7.633 MPa。
可以看出,同一工况下,推进轴系不同部件产生最恶劣工作环境时对应的冰载荷加载位置不同,即不同轴段处产生最大轴系扭振响应结果时对应的冰载荷激励的初始相位角不同。
不同工况间轴系瞬态扭振特性相差较大。这说明在实际分析时,针对轴系扭振系统中不同部件的不同扭振特性,均需要找出最恶劣状态下对应的冰载荷初始相位角和对应的冰载荷工况。
通过上述分析可以看出工况2时推进轴系的扭振情况最为恶劣,现针对工况2时的轴系瞬态扭振特性继续进行研究。在工况2条件下,冰载荷激励在16°时加载对应的螺旋桨轴瞬态扭矩图和冰载荷激励在76°加载时对应的后轴系部分各轴段最大应力图如图11和图12所示。从图中可知,加载冰载荷激励后螺旋桨轴扭矩有较大突变,瞬时扭矩远超稳定时扭矩值;后轴系最大应力出现在轴段八处。
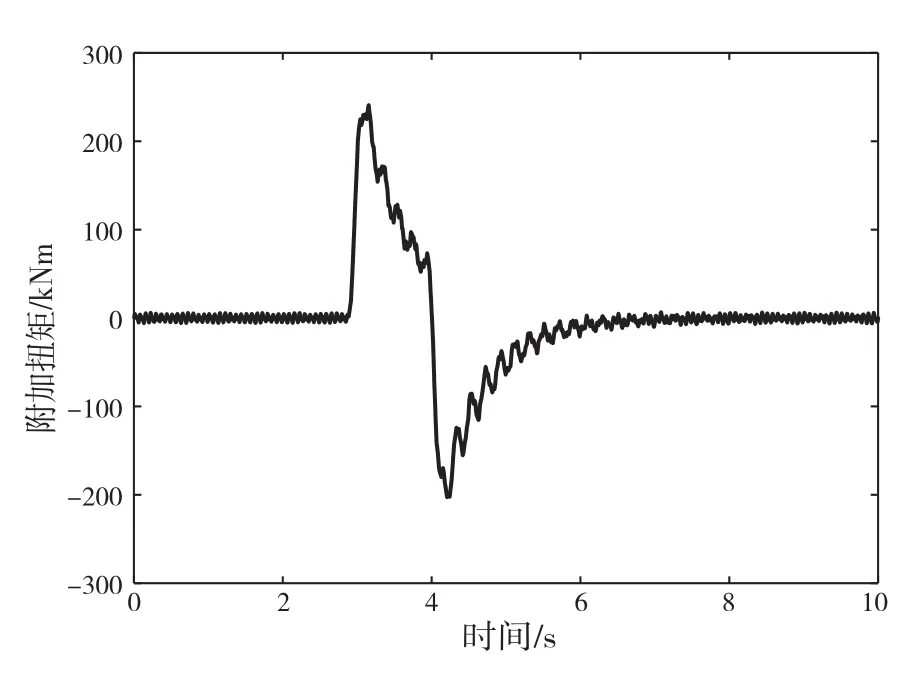
图11 工况2螺旋桨轴扭矩时域
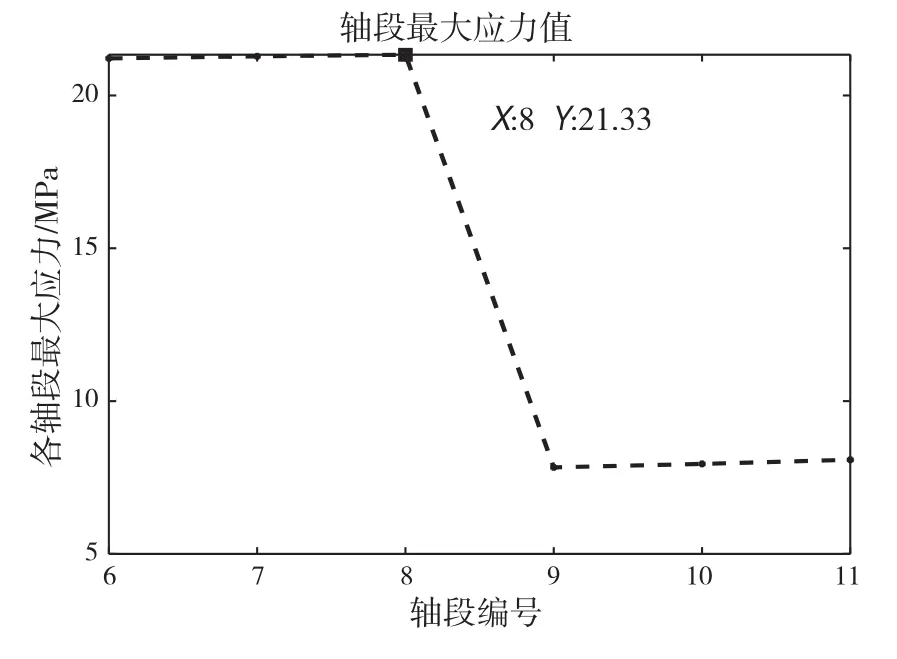
图12 工况2后轴系各轴段最大应力
3 轴系扭振敏感性分析
从上文计算结果可知,冰载荷下的轴系瞬态扭振响应结果远大于无冰载荷激励时的稳态结果。这就对轴系扭振系统里重要部件(如弹性联轴器以及螺旋桨轴等)的工作特性提出了更高的要求。故本文特进行轴系扭振敏感性分析,选取两个轴系扭振参数:弹性联轴器刚度和离合器惯量,探究弹性联轴器附加扭矩、螺旋桨轴附加扭矩和后轴系轴段(选取轴段八分析)最大应力对上述两个参数变化的敏感性。
现分别取上述两个参数原始设计值的40%、60%、80%、100%、120%、140%、160%、180%和200%,计算得到的结果如图13 -图15所示。
由图可知:弹性联轴器扭矩、螺旋桨轴扭矩和后轴系轴段最大应力均对弹性联轴器刚度的变化较为敏感,对离合器惯量的变化敏感性较差。
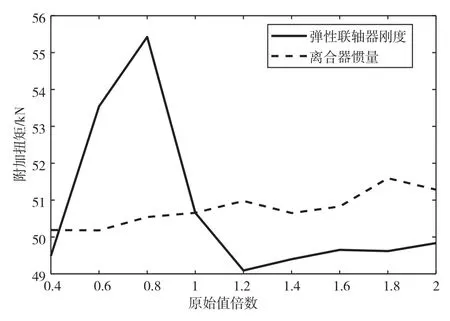
图13 弹性联轴器扭矩敏感性
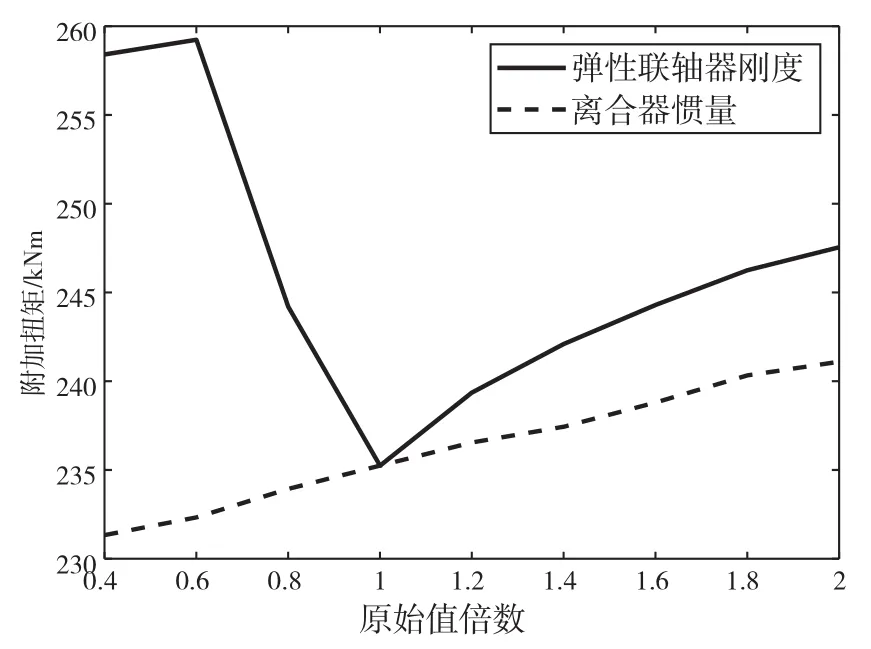
图14 螺旋桨轴扭矩敏感性
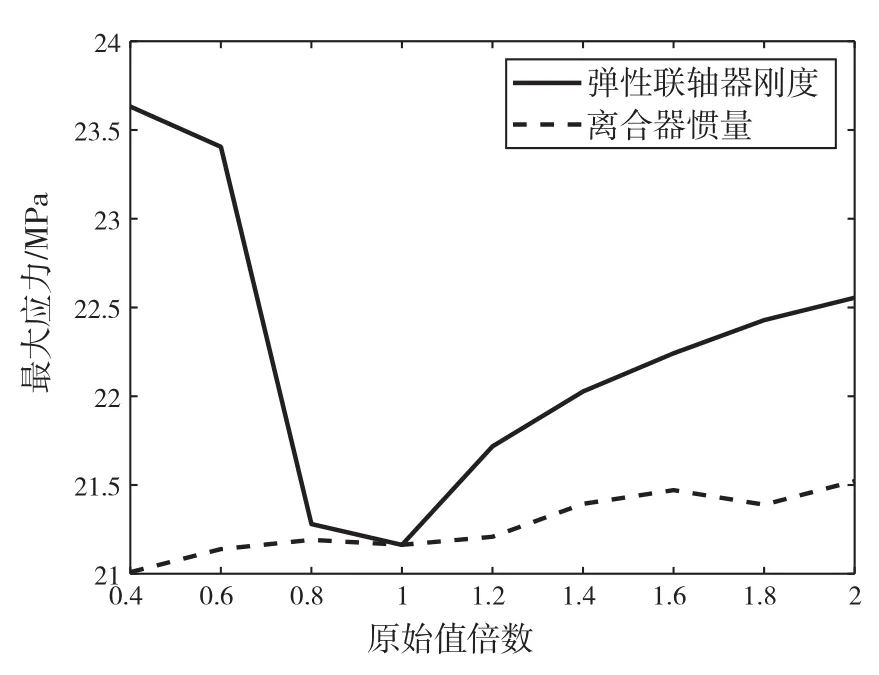
图15 后轴系轴段最大应力敏感性
4 结 语
本文通过建立轴系扭转振动分析模型,采用时域计算方法,对比分析有无冰载荷作用及不同工况冰载荷作用下的轴系瞬态扭振特性,主要结论如下:
(1)通过对比发现冰载荷激励对轴系瞬态扭振特性影响较大;
(2)冰载荷初始相位角对轴系瞬态扭振特性有较大影响,实际考虑时应先找出对轴系扭振影响最大的初始相位角;
(3)不同工况下的冰载荷激励对轴系瞬态扭振特性的影响有较大区别,实际考虑时应找出对轴系扭振影响最大的工况;
(4)推进轴系中不同部位对应的扭振特性不同,具体分析时应综合考虑最恶劣的冰载荷初始相位角和冰载荷工况;
(5)冰载荷激励下轴系瞬态扭振特性对联轴器扭转刚度比较敏感,因此轴系中的联轴器刚度匹配值得特别重视。
