空间对接锁系精密钢索张拉形变规律试验研究
2020-07-02许春田吴鑫杨徐正东
许春田,吴鑫杨,徐正东,王 朋
(1. 辽宁科技大学机械工程与自动化学院, 鞍山114051; 2. 上海宇航系统工程研究所,上海201109)
1 引言
航天器交互对接的关键对接机构[1]主要是由2 套锁系组成的一个闭环传动系统,每套锁系中只有一把为主动锁,通过钢索经导向轮与其它被动锁串联(见图1)。 锁系对接是钢索进行精密传动的一种控制形式[2-3],其同步性直接决定着两航天器能否顺利实现交会对接,是航天器交会对接的关键技术[4]。
受空间环境条件的制约,锁系对接同步性主要通过装配过程中对其串联钢索预紧载荷的调节来保证。 由于在这方面缺少必要的理论指导,主要凭经验、反复操作来保证,不仅装配效率低、成本高,而且保证困难。 针对这一问题,不少学者开展了大量研究并提出了一些改进措施,如谭益松[5]、潘东[6]等分别对空间大型末端执行器的钢索捕获动力学行为及特性进行了建模与仿真;李建广等[7]建立了锁系轮系传动同步性模型;肖杰等[8]采用仿真方法对分析了锁系运动同步性影响的主要因素,并提出了改进方向;张华等[9]通过锁系驱动过程仿真,提出了改进索驱轮系运动同步性的建议;黄铁球等[10]建立了单锁数学模型,通过ADMAS 仿真分析了预紧力对锁系同步性的影响;郑云青等[11]建立了锁系运动同步性与钢索弹性变形间的关系模型,并提出了降低钢索张力和形变量的控制方向。 然而,这些研究主要从锁系对接运动学方面开展,并没有涉及钢索形变的影响。 锁系串联钢索的连接结构及钢索特性决定了其装配是一个预紧载荷不断施加与不断调节的过程。 许春田等[12]虽从装配方面对锁系钢索蠕变行为的影响进行了研究,但主要针对蠕变稳定阶段,尚未论及非稳定阶段钢索形变的影响,并不完整。
为此,本文主要针对空间锁系装配预紧载荷施加过程中,因受钢索蠕变、内部丝、股及绳轮间摩擦和转角等因素引起张力松弛[13]而影响装配精度及效率问题,对其钢索形变规律开展试验研究,以实现预紧载荷的有效控制与补偿。
2 钢索形变试验
2.1 试验原理
试验系统组成如图2 所示。 钢索(3)在主、被动绳轮组件(5)、(1)间通过锁紧螺母(6)进行固定,主、被动绳轮(12)、(13)半径都为75 mm,其周缘刻度(8)分别用于记录转过的角度,被动绳轮(13)通过销轴(11)实现固定。 减速器(9)通过联轴器与主动绳轮组件(5)联接,通过驱动主动绳轮(12)实现钢索预紧载荷的施加,其大小则由两导向轮(14)、(15)间钢索(3)上装有的张力仪(2)进行读取。 每一位置测定时,因被动绳轮转角θ2固定,根据锁系实际装配需求,预紧载荷对应的形变则用主动绳轮转角θ1与其初始角的差值,即转角偏差Δθ来表示。 由于锁系装配主要对其啮合和锁紧两位置处的精度进行控制[7-9],为此,试验在其对应绳轮转角分别为60°(啮合)和180°(锁紧)处展开。
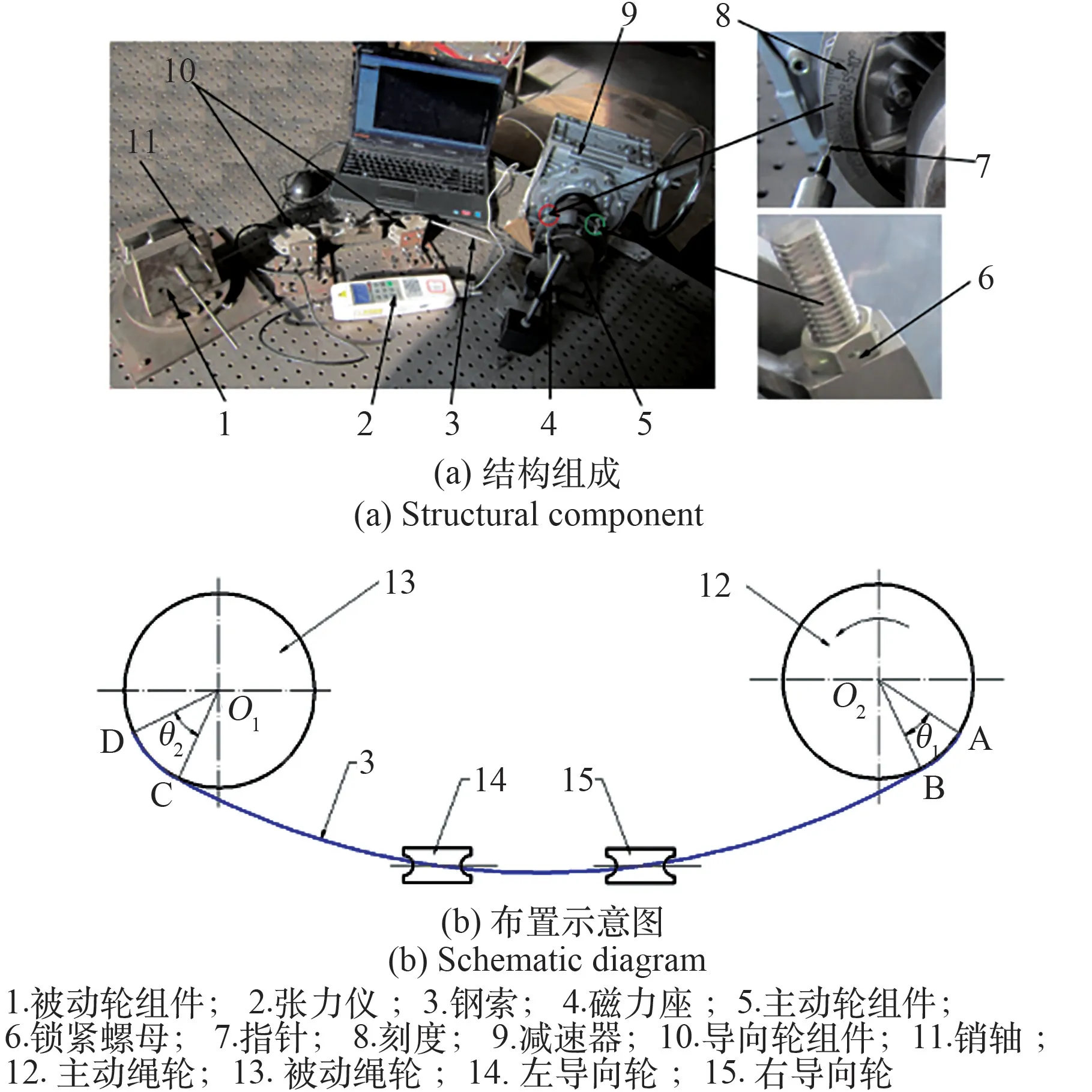
图2 试验系统Fig.2 Experiment system
2.2 试验样本
钢索在载荷作用下会发生弹性、粘弹性、粘塑性及塑性等复杂的变形[14],在锁系装配过程中,如果不加以控制,将导致其串联钢索在预紧载荷作用下出现松弛而影响其对接同步性。 因不同结构及材质的钢索在预紧载荷作用下所表现出的形变行为有所区别[15],为具有针对性,本研究试验样本均为航天用类型为6x19 s+IWS、1Cr18Ni9Ti钢索, 其力学性能及结构参数分别见表1。

表1 钢索力学性能及结构参数值Table 1 Mechanical performance and structure parameters of the cable
为降低测量误差,以更精确地分析不同工况条件下钢索形变行为,试验以3 组钢索为样本,每组包括2 根,分别用于锁系啮合与锁紧两位置处钢索形变行为的研究。 其中,样本第1 组钢索未经预张拉;第2、3 组分别为预先经过24 h 和48 h采用500 kg 配重进行静力加载预张拉。 按照图3显示加载时程,并考虑钢索松弛行为,分别以间隔5 min、2 h、5 h 和24 h 采用缓慢加载保压方式进行预紧载荷的施加及试验数据的测定。
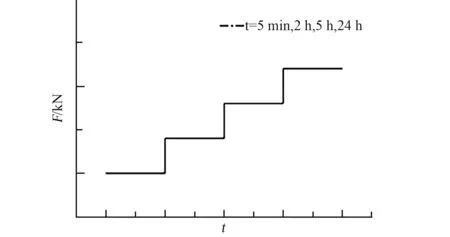
图3 预紧载荷加载时程Fig.3 Preload time-history
2.3 张拉工艺
1)调节钢索两端锁紧螺母,使主动绳轮(12)上钢索固定端A 在其入口B 处对应转角θ1为0°,张力仪(2)显示的预紧载荷为0.2 kN 后, 将指针(7)指向绳轮上的某一刻度作为初始基准。
2)通过减速器(9)驱动主动绳轮(12)相对初始基准转过60°,用销轴(11)固定被动绳轮(13),并将指针指定值作为60°位置数据测定的基准。
3)分别以间隔5 min,通过缓慢施加保压方式施加预紧载荷直至3 kN,记录每次张力仪显示值及指针对应的刻度,则相应的钢索形变就是该刻度值与60°基准值间的差值。
4)同步骤3,分别完成以间隔2 h、5 h 和24 h保压延时加载方式下的钢索形变数据的采集。
5)安装第2 根钢索,在步骤1 基础上,驱动主动绳轮旋转到180°,同步骤3 ~4,完成转角180°处其形变数据的采集。
6)依据上述步骤1 ~5,分别完成3 组钢索样本数据的采集。
为降低因钢索初始长度差异导致初始基准不同而引起的测量误差的影响,在3 组钢索形变数据采集前,先以第1 组中的第1 根钢索按上述步骤1 设定的初始基准进行数据的采集,而在进行其它钢索数据采集时,可分别通过绳轮两端锁紧螺母的调节,使其初始基准分别与第1 根钢索初始基准的设定值相等,这样就确保了3 组钢索测量的初始工作长度都相等。
2.4 数据分析
在分别对绳轮转角60°与180°处以5 min、2 h、5 h 和24 h 间隔加载保压的钢索形变行为研究时,经观察:在给定预紧载荷作用下,以超过24 h间隔加载保压,钢索形变基本不再发生变化。因而为便于分析,将以24 h 间隔测定的数据作为其它间隔加载数据的标准,则以上述时间间隔加载保压方式下,3 组钢索测控点预紧载荷与主动绳轮转角偏差关系如图4 所示。
从图4 可以看出,受钢索丝、股及绳轮间摩擦力作用、转角及蠕变等因素影响,不同间隔时间加载方式下,即使预紧载荷相等,对应的转角偏差也不相等。 3 组钢索存在着随间隔加载时间的增大,转角偏差与对应的预紧载荷间的变化曲线都呈现逐渐接近标准曲线,且变化率逐渐变小的趋势,这说明钢索稳定性能逐步提高,在装配中易获得较高精度。 另外,通过对每根钢索不同时间间隔对应的4 条曲线变化规律分析还可发现,在相等预紧载荷作用下,加载间隔时间越短,3 组钢索对应的转角偏差就越大,间隔时间越长,转角偏差就越小,越接近标准值。 这主要是因为连续加载间隔时间短时,钢索发生的主要为弹性形变;随着间隔加载保压时间的增大,钢索蠕变、丝、股及绳轮间微动摩擦等因素的影响逐步增大,导致钢索松弛而产生张力损失,从而测定的数据减小;但超过24 h 后,因钢索内部丝、股间结构重新排列均匀,相互间基本不再产生滑移及蠕动磨损现象,致使钢索内部张力基本不再发生变化,对应的形变也基本保持稳定。
通过对比图4 的3 组结果可以看出,未经预张拉的钢索第1 组与经预张拉的第2、3 组相比,不同时间间隔间内其转角偏差随预紧载荷变化波动范围相对较大。 这主要因为预经张拉的钢索,其内部残余应力得到大部分消除及丝、股间排列变得较均匀,性能较稳定,而未预张拉的钢索,不仅性能稳定性较差,而且还产生较大结构伸长,经计算其结构伸长率达0. 2%,如果直接用于锁系对接,必定会对其装配及传动精度产生较大的影响。 而另外经预张拉的两组绳索结构伸长并不明显,相等预紧载荷作用的形变虽所区别,但相差不大,经计算最大误差不超过10%,这主要受钢索本身的物理特性及结构差异造成的。
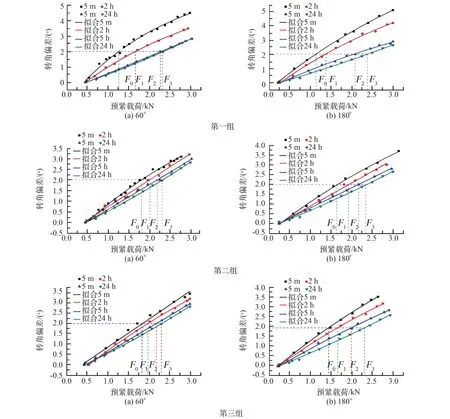
图4 转角60°和180°处3 组钢索形变与预紧载荷变化规律Fig.4 Law of deformation and preload in three groups of cables at 60 ° and 180 °
此外,从图4 中还可看出,不同转角对钢索形变也有一定的影响,在测控点预紧载荷相等条件下,呈现转角越大,对应的转角偏差反而越小的现象。 这主要因为施加的载荷在从主动绳轮钢索固定端经钢索传递到预紧载荷测控点过程中,随着主动绳轮转角的增大,钢索与绳轮间接触弧长逐渐变长,相互间产生的摩擦力相应地增大,导致钢索张力损失相对变大,从而实测值相对变小。 因而,对于锁系对接过程中的啮合与锁紧两位置,因对应的转角值不等,为保证对接同步性,应分别对其装配精度进行控制。
3 形变补偿
空间锁系对接同步性,主要通过装配过程对钢索施加一定预紧载荷抵消其驱动过程中的形变来控制。 然而,通过上述分析可以看出,受钢索加载时间间隔及转角等因素影响,相同操作条件下,相等转角偏差对应的预紧载荷并不相等,呈现加载时间越短,预紧载荷就越小,其在标准曲线(24 h)上对应的转角偏差就越小的规律。 因而相对于标准曲线对应的预紧载荷来讲,补偿的张力就越大。 随着间隔加载保压时间变长,预紧载荷不仅受钢索微动蠕变的影响变大,而且还受其从主动绳轮钢索固定端传递到测控点过程中的转角、丝、股与绳轮间摩擦力作用等因素影响而产生损失,导致松弛而引起新的转角偏差,致使不同间隔加载方式下的转角偏差曲线并不重合,而且转角越大越明显。 例如,对于给定转角偏差2°在标准曲线上对应的载荷为F3,如果以间隔5 min 进行加载,则钢索测控点处预紧载荷在达到F0就能即时满足要求,然而,随着分别经历2 h 和5 h 间隔加载保压,该转角偏差对应的预紧载荷F1、F2却逐步增大,分别相对于标准载荷F3的差值,即补偿值F3-F1、F3-F2则逐渐变小,相应地,钢索稳定性能逐渐得以提高。
为预测锁系装配过程中不同预紧载荷作用下张力损失补偿值,针对上述以不同时间间隔加载方式下测定的经预张拉的第2、3 组钢索预紧载荷与转角偏差的平均值,分别在60°和180°转角处根据其变化规律对其用指数曲线进行拟合,其拟合曲线可统一表示为式(1):
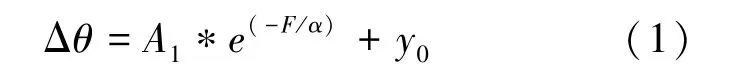
式中,Δθ为转角偏差(°),F为预紧载荷(kN),其它各参数为常数分别见表2。

表2 预紧载荷与转角偏差拟合方程参数值Table 2 Parameter values of fitting equation between preload and angle deviation
式(1)化简可得式(2),即用于预测主动绳轮转角60°与180°处以上述不同时间间隔加载方式下转角偏差对应的预紧载荷施加值。

则在转角偏差Δθ条件下,分别在转角60°和180°处,以间隔5 min、2 h 和5 h 施加预紧载荷相对于24 h 标准值的差值,即装配中预紧载荷损失补偿值的预测模型可分别表示为式(3)、(4),经与实测值相比较,两者误差在0.1%以内,如表3、表4 所示。
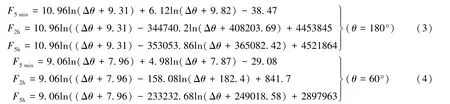
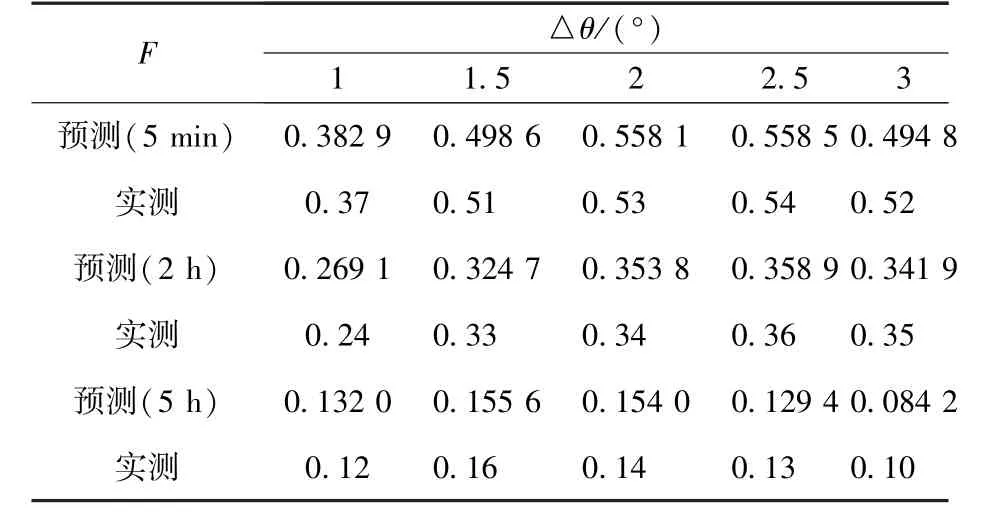
表3 锁系啮合位置不同时间间隔加载方式下预测值与实测值比较Table 3 Load comparison between prediction and measured values at meshing position of the locks under different time intervals/kN
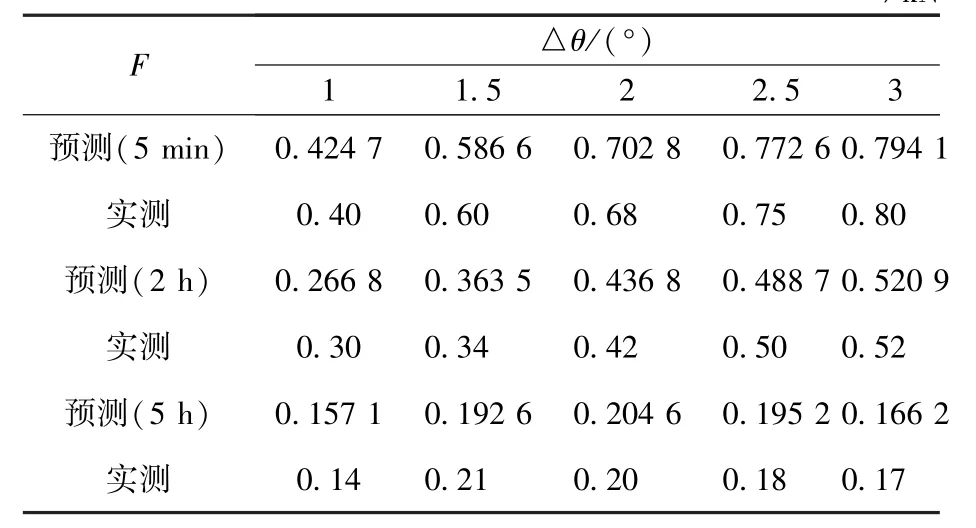
表4 锁系锁紧位置不同时间间隔加载方式下预测值与实测值比较Table 4 Load comparison between prediction and measured values at locking position of the locks under different time intervals/kN
4 结论
1)针对空间对接锁系装配工况,通过对不同预张拉处理3 组钢索样本的试验研究,建立了不同时间间隔加载方式下以绳轮转角偏差表示的钢索形变与预紧载荷间的数学方程,并分析了预处理、不同间隔加载方式和转角等因素的影响。
2)建立了一个预紧载荷补偿的预测模型,该模型能较精确地反映不同时间5 min、2 h 和5 h间隔加载条件下为满足装配精度要求所对应的预紧载荷损失补偿值,可为锁系装配效率的提高提供一定参考。
