预压缩对离心压气机级效率的影响

白欢

摘   要：为了研究预压缩叶型扩压器对离心压气机级效率的影响，本文利用数值仿真技术对具有不同预压缩角和进口几何角的扩压器进行了设计和研究。结果发现，当预压缩角一定时，在一定范围内，随着进口几何角的增加，扩压器的峰值效率逐渐增加。在进口几何角一定时，随着预压缩角的增加，扩压器的峰值效率先迅速增加后增速放缓最后下降。在预压缩角和几何角的共同作用下，通过调节预压缩角和几何角，可以有效地提高扩压器的性能，使压缩机级最高效率超过 84.4%;且进口几何角越小，需要越大的预压缩角，才能达到最大的峰值效率。

关键词：扩压器  预压缩角  进口几何角  离心压气机

中图分类号：TH45                                  文献标识码：A                        文章编号：1674-098X（2020）04（c）-0098-05

1  引言

离心压气机广泛应用于航空、石化等工业中，随着我国工业技术的不断发展，人们对压气机的气动性能的要求也越来越高。在高负荷离心压气机中，径向叶片式扩压器因其高效率特性而成为设计的热点。长久以来，研究者们针对叶片式扩压器进行了大量的研究。Deniz[1]等人研究了扩压器入口流动条件对扩压器性能的影响。Ubber 等人[2-5]研究了叶片式扩压器进口几何角对压气机性能的影响，并给出了扩压器出口附近的详细流场。预压缩叶型是控制轴流压气机激波的一种有效方法[6-8]，但在离心压气机扩压器中很少应用。因此，研究扩压器的进口几何角和预压缩角对压气机的效率的影响，具有十分重要的意义。

2  离心压气机

本文以美国宇航局设计的高负荷单级离心压气机作为研究对象。表1列出了该压气机的主要几何和空气动力学参数。压气机的流动路径和叶片形状由McKain和 Holbrook提供[9]。

3  预压缩叶型扩压器

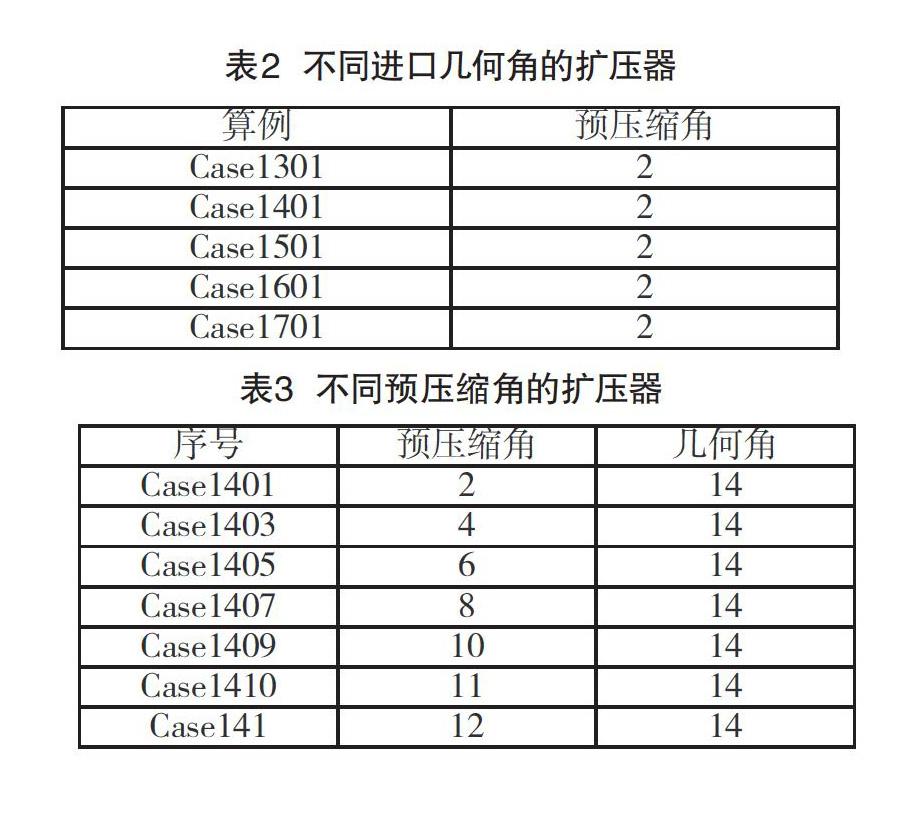
图1为带有预压缩叶型的扩压器的造型示意图。其中，扩压器叶片的压力面型线由直线（1-5）、直线（5-7）以及圆弧（7-9）组成，吸力面型线由圆弧（1-4）、直线（4-6）以及直线（6-9）组成，其中点4为圆弧与相邻直线的切点。直线（3-5）与直线（5-10）之间的夹角为通道扩张半角（θ3）。圆弧（1-4）之間的转折角定义为预压缩角（）。直线（3-4）和直线（5-6）之间的距离定义为喉部的长度（）。线段（3-4）的长度为喉部宽度（）。通过调整点4的在直线（3-4）上的位置来改变预压缩角度的大小，直线（1-5）与圆弧（1-4）在前缘点的角平分线与该点切向方向的夹角为进口几何角（β）。

4  数值方法与验证

4.1 数值方法

数值计算采用了Numeca商业CFD软件，采用Jameson的有限体积差分格式并结合Spalart-Allmaras湍流模型相对坐标系下的三维雷诺平均Navier-Stokes方程进行求解，采用显式四阶Runge-Kutta法时间推进以获得定常解，为提高计算效率，采用了多重网格法、局部时间步长和残差光顺等加速收敛措施，离心压气机级总网格数约160万。

边界条件给定如下：进口边界给定总压、总温和绝对气流角;出口边界条件只给定平均静压;壁而采用了绝热无滑移边界条件，与转子叶片连接的轮毅壁和叶片壁转动，而轮毅壁的其他部分以及机匣壁则定义为静止，在叶轮和扩压器通道交接而采用混合平面法进行信息传递。

4.2 数值方法验证

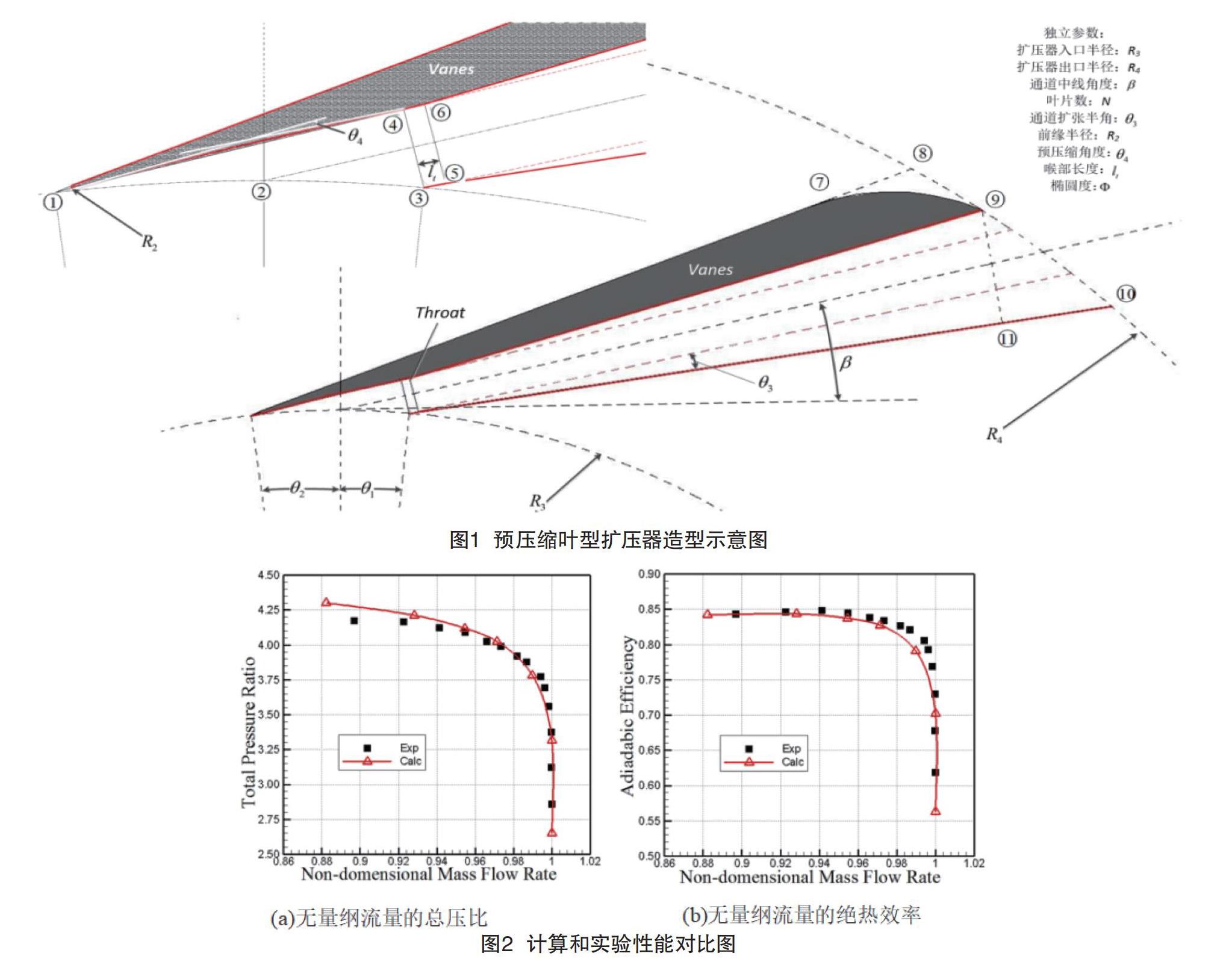
图2为原型离心压气机和数值计算级性能的比较。计算得到的堵塞质量流量比实验结果[10]大2.18%。从总压比和绝热效率与无量纲流量的关系图可知，压气机级的总压比和绝热效率在喘振附近和设计工况附近都高于实验值，喘振附近绝热效率与实验值吻合较好，同时数值计算的喘振裕度比试验数据的喘振裕度要宽。整体上看，计算结果与实验数据吻合较好。因此，数值方法可以预测高负荷离心压气机级内所有重要的流动现象，适用于叶片式扩压器的研究。

5  结果与讨论

5.1 进口几何角对级效率的影响

为了探究进口几何角对预压缩叶型扩压器效率的影响，本文首先研究了预压缩角=2°的情况下，不同的进口几何角（β）对压气机效率的影响，由于叶轮出口的平均气流角约为15°，因此，共设计了5个不同入口几何角的扩压器（见表2）。为了排除其他因素的影响，表中所有扩压器的入口半径R3=226mm，当量扩张半角θ3=4°。不同进口几何角的扩压器级效率如图3所示。

由图1可知，在其他重要参数保持不变的情况下，随着扩压器进口几何角的增加，扩压器的喉部面积会逐渐增大，因此堵塞流量也逐渐增大，效率曲线右移（见图3）。从图中还可以看出，随着进口几何角的增大，扩压器的峰值效率逐渐增大，但当几何角超过 16°后，压气机在偏离峰值工况后效率 下降很快。综合来看，当扩压器入口安装角在叶轮出口平均气流角附近，即扩压器进口几何角在14～16°之间，压气机整体性能较好。

峰值工况下，不同进口几何角扩压器峰值点 50%叶高的绝对速度矢量分布情况如图4所示。由图可知，随着几何进气角的增加，扩压器半无叶区绝对速度的变化很小，说明在一定的范围内，几何进气角的变化对半无叶区的流场影响不大。 但当气流经过半无叶区后，由于进口几何角较小的扩压器，其喉部面积也相对较小，因此气流在喉部前后减速缓慢，尤其是吸力面的高速气流几乎占据了整个喉部，如图4（a），这将造成较大的冲击损失，并加速压力面的流动分离，不利于压气机效率的提高。随着进口几何角的增加，扩压器喉部面积逐渐增大，通流能力增强，高速气流在喉部前后减速充分，并延缓了压力面的流动分离，如图4（b）、4（c）。因此，在一定范围内，随着进口几何角的增加，压气机级的峰值效率逐渐增加。

5.2 预压缩角对扩压器效率的影响

为了探究预压缩角对扩压器效率的影响，本文研究了进口几何角β=14°的情况下，不同的预压缩角对压气机级的效率影响，设计了7个不同预压缩角的扩压器，见表3。为了排除其他因素的影响，表中所有扩压器的入口半径 R3=226mm，当量扩张半角（θ3）=4°。扩压器不同进口几何角的压气机级性能如图5所示。

由图可知，随着预压缩角度的增加，堵塞流量逐渐增加，曲线右移，但变化幅度较小，根据图1可知，这主要是由于预压缩角变化引起的喉部面积变化较小。从图还可以看出，随着预压缩角度的增加，峰值效率先迅速增加然后增速变缓最后下降，这种变化在图6 展示的更清楚。

不同预压缩角扩压器在50%叶高的马赫数分布情况如图7所示。由图可知，随着预压缩角度的增加，半无叶区的马赫数逐渐降低，这将有利于减小气流对半无叶区的冲击损失。此外，从图中的马赫数等值线可以看出，随着预压缩角度的增加，气流经过喉部后的流动更加均匀，这将有利于减小压力面和吸力面压差，削弱二次流动的强度，使流动分离延后。因此随着预压缩角度的增加，扩压器的效率逐渐增加。但过多的增加预压缩角，一方面不能进一步明显改变流动的均匀性，另一方面预压缩角度增加，还会增加气流在半无叶区的流程，造成额外的沿程损失，不利于扩压器效率的提高，因此当预压缩角度为11°时候，扩压器效率达到最佳。

图8为不同预压缩角的扩压器的相对马赫数在半无叶区吸力面的变化情况。从图中可以看出，当预压缩角较小时，气流在半无叶的最大马赫数较高，说明气流在半无叶区的减速并不充分，冲击损失较大，因此1401的效率较低。从图中 还可以看出，1401 与 1405 的最大相对马赫数之差大于 1405 与 1410，说明当来流速度较大时，预压缩对来流的缓冲作用更加明显。即当预压缩角较小时，半无叶区的气流速度较大，冲击损失较大，此时将预压缩角度增加 1 °，能够明显减小来流对半无叶区的冲击损失。而随着预压缩角的增加，来流在半无叶区的马赫数逐渐降低，冲击损也相应较小，此时再将预压缩角度增加 1 °，对效率的提升就会相对较小。此外，增加预压缩角也会增加半无叶区的沿程损失。在上述原因的共同影响下，随着预压缩角的增加，效率呈现先迅速增加后增速放缓最后下降的变化情况。

5.3 几何角和预压缩共同对级效率的影响

由前可知，扩压器的入口几何角和预压缩角都对扩压器的效率具有重要影响。当扩压器的进口几何角在14～16°之间时，级的性能最好，而在进口几何角一定时，扩压器存在最佳的预压缩角。为了探究进口几何角和预压缩角共同對压气机级的影响，本文分别研究了14～16°下，不同预压缩角对压气机级效率的影响，如图9所示。

由图9可以看出，当进口几何角分别为14、15、16 时，随着预压缩角的增加，扩压器的效率均呈现逐渐增加后减小，且增长速度先快后慢的趋势，其原因如 5.2 节所述。由于预压缩角和几何角都对离心式压气机级的效率有影响，根据图9，做出预压缩角和进口几何角与峰值效率的云图，如图10所示。由图10可知，在预压缩角一定时，可以通过调节进口几何角来提高级效率，当进口几何角一定时，可以通过调节预压缩角来提高级效率，且由图还可知，当几何角较小时，要达到峰值效率，需要更大的预压缩角。这主要是因为几何进气角较小时，扩压器半无叶区的气流速度较高。因此，为了将来流充分减速，使流动达到最佳的流动状态，需要更大的预压缩角。综合来看，通过调节预压缩角和几何角，可以有效地提高扩压器的性能，使压缩机级最高效率超过 84.4%，如图10中红色区域所示。

6  结语

本文对预压缩叶型扩压器对压气机级效率的影响进行了研究，主要结论如下所述。

（1）当预压缩角一定时，在一定范围内，随着进口几何角的增加，扩压器的峰值效率逐渐增加。

（2）在进口几何角一定时，随着预压缩角度的增加，扩压器的峰值效率先迅速增加后增速放缓最后下降，存在最佳的预压缩角。

（3）在预压缩角和几何角的共同作用下，通过调节预压缩角和几何角，可以有效提高扩压器的性能，使压缩机级最高效率超过 84.4%;且进口几何角越小，需要越大的预压缩角，才能达到最大的峰值效率。

参考文献

[1] Deniz A， Greitzer E M， Cumpsty N A. Effects of Inlet Flow Field Conditions on the Performance of Centrifugal Compressor Diffusers： Part 2-Straight-Channel Diffuser. ASME Journalof Turbomachinery，2000，122（1）：11-21.

[2] Ubben S and Niehuis R. Experimental Investigation of the Diffuser Vane Clearance Effect in a Centrifugal Compressor Stage with Adjustable Diffuser Geometry：Part-Ⅰ Compressor Performance Analysis. ASME Paper，GT2014-26896， 2014.

[3] Ubben S and Niehuis R. Experimental Investigation of the Diffuser Vane Clearance Effect in a Centrifugal Compressor Stage with Adjustable Diffuser Geometry： Part Ⅰ- Detailed Flow Analysis. ASME Paper， GT2014-27175， 2014.

[4] Wang Y， et al. The Influence of Wedge Diffuser Blade Number and Divergence Angle on the Performance of a High Pressure Centrifugal Compressor. Journal of Thermal Science，2018，27（1）：17-24.

[5] Han G， Lu X， Zhao S， et al. Parametric Studies of Pipe Diffuser on Performance of a Highly Loaded Centrifugal Compressor[J]. JOURNAL OF ENGINEERING FOR GAS TURBINESAND POWER-TRANSACTIONS OF THE ASME， 2014， 136（12）：122604.

[6] Graham R C， Klapproth J F， Barina F J. Investigation of Off-design Performance of Shock in-rotor Type Supersonic Blading. NACA-RM-E51C22， 1951.

[7] Fleeter S， Holtman R L， McClure R B， et al. Experi-mental Investigation of a Supersonic Compressor Cas-cade. ARL-TR-75-0208， 1975.

[8] Alistair J， Shahrokh S and Ning Q， Alleviation of Shock-Wave Effects on a Highly Loaded Axial Compressor Through Novel Blade Shaping， ASME Paper，GT2016-57550， 2016.

[9] McKain T F and Holbrook G J. Coordinates for a High Performance 4：1 Pressure Ratio Centrifugal Compressor. NASA Contractor Report 204134， 1997.

[10]Chaolei Zhang， Qinghua Deng， and Zhenping Feng. Study on aerodynamic redesign of a high pressure ratio centrifugal compressor. ASME Paper， GT2010-23714.