基于粒子群优化极限学习机的中长期电力需求预测研究

王 婷，刘婷婷

(华北电力大学 经济与管理学院，河北 保定071000)

随着我国经济进入新常态，经济由高速增长转入中高速增长，经济结构优化升级，第二产业内部结构不断优化，传统高耗能行业比重下降，中高端制造业呈现上涨态势，经济增长由要素驱动、投资驱动转化到创新驱动与服务业发展。因而，伴随产业结构的调整、经济增长点的变化，三次产业用电量、比重均会产生一定的波动，研究和预测新形势下的我国中长期电力需求，也有助于电网科学合理的投资规划，具有重要的理论意义与现实意义。因而，电力需求预测一直是国内外学者关注的重点，以往关于经济与电力需求预测的研究，选取的指标较少、多数预测模型也较为传统，不能全面的反应宏观经济特征，也难以将完善的变量纳入到研究模型，再加上年电力负荷的非线性特征，预测难度高，精度较难得到保证。

电力需求与经济发展关系研究所采用的研究指标中，电力需求弹性系数、用电量增速是最普遍使用的指标。单葆国的研究采用电力需求弹性系数探讨了改革开放以来经济发展与电力需求的关系[1]。王韶华的研究发现经济增长、人口增长、城市化以及节能和碳排放约束是推动电力需求增长的主要因素，其中经济增长和城市化对电力需求的影响较大[2]。吴立军、王何舟等的研究运用主成分分析法得出了对电力负荷最优影响力的三个经济指标是人均全部收入、人均可支配收入和人均全部支出[3]。此外，产业结构比重、全社会用电量、GDP增长率、全社会用电结构、电力需求增长率也为较为普遍使用的指标。我国学者林伯强的研究指出GDP、资本存量、人力资本以及电力消费之间存在着长期均衡关系[4]。

在电力需求预测上，研究主要从以下两个方面展开：其一，从电力需求与经济发展的关系出发，使用协整分析、误差修正模型等方法确定电力需求与经济的关系，基于得出的关系建立需求函数、模型，对电力需求加以预测。蒋惠凤，何有世等的研究考虑到了影响电力需求的经济因素之间存在的多重共线性，使用偏最小二乘的方法去除了多重共线性的影响并建立了预测模型[5]。其二，是运用历史的用电量数据的时间序列变化规律，运用主成分分析、回归预测、灰色预测、支持向量机、神经网络等方法预测电力需求[6]。赵海清的研究提出了一种基于累积法的GM预测模型，该模型能克服灰色预测模型运算复杂、精度较低的缺陷[7]。李冬辉，尹海燕，郑博文使用多种群的果蝇优化算法(MFOA)和广义回归神经网络相结合的混合年电力负荷预测模型，有效的提高了预测精度，且能够避免预测结果陷入局部最优[8]。Takeda H等提出了一种新的电力负荷建模框架，将集合卡尔曼滤波器与收归/多元方法结合，不仅预测精度显著提高，而且可以提供详细的分析信息[9]。

本文选取了影响电力消费的6类共24个因素，以因子分析提取的影响我国电力需求的因素为自变量，以电力消费量为因变量，使用改进的粒子群算法优化的极限学习机对电力需求进行预测。

1 预测方法与模型

1.1 改进粒子群

粒子群优化的优势在于需要调整的参数较少，简单易实现且很适合处理优化问题。粒子在空间飞行时，有速度和位置两大特征，经过每次迭代，粒子i第j维的速度vij和位置xij按如下表达式更新：

vij(t+1)=vij(t)+c1r1j(t)(pi j-xij(t))+c2r2j(t)(pgj-xij(t))

(1)

xij(t+1)=xij(t)+vij(t+1)

(2)

为减少随机搜索时间，同时提高粒子群算法的优化效果，本文针对标准粒子群算法进行改进，即通过惯性权重递减策略改进公式(1)，速度更新公式为(4)。

w=wmax-t(wmax-wmin)/itmax

(3)

vij(t+1)=wvij(t)+c1r1j(t)(pi j-xij(t))+c2r2j(t)(pgj-xij(t))

(4)

在权重更新公式(3)中，wmax代表最大搜索权重，其值为0.8；而wmin则代表最小搜索权重，其值等于0.2。另外，itmax代表最大迭代次数，根据精度需要，其值设置为100，t表示当前迭代次数。

1.2 极限学习机

极限学习机(Extreme Learning Machine)是求解单隐层神经网络的算法，其本质是求解最小二乘解，参数设置简单，能在保证运算精度的同时拥有较快的学习速度，被广泛的应用于回归、检测、分类等若干领域。然而，极限学习机也存在某些方面的缺陷：其一，隐含层节点的设置较为困难；其二，存在着非优化或不必要的权重值与阈值降低极限学习机性能的情形。

1.3 基于粒子群优化极限学习机

针对极限学习机本身存在的问题，本文使用粒子群优化极限学习机，有力地改进了极限学习机存在的问题，通过网络中权值和阈值的更新得到最优网络。在第一部分，使用因子分析提取输入变量；第二部分，使用粒子群优化算法优化网络结构的权值和阈值；第三部分使用训练后的极限学习机进行预测。

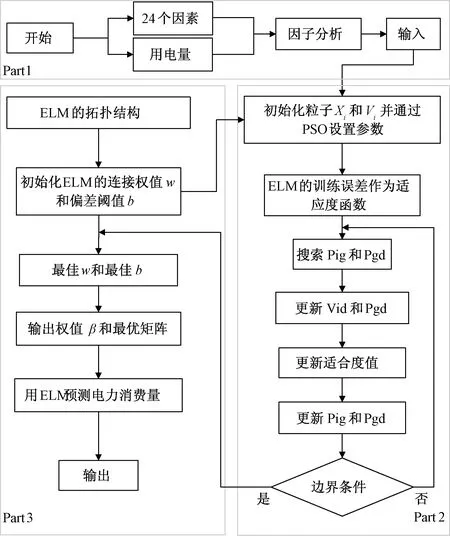
图1 电力需求预测流程

2 数据分析

2.1 数据变换与因素预选

本文主要研究1995-2015年我国中长期电力负荷预测及其影响因素，主要从社会经济的角度分析影响我国中长期电力需求的因素并对未来我国电力需求进行预测。

因此本文确定的主要影响电力需求的24个因素包括：GDP，全社会固定资产投资，第一产业用电量，第二产业用电量，第三产业用电量，年末总人口，人均生活用电量，进出口总额，农村居民消费水平，城镇居民消费水平，城镇人均可支配收入，农村人均纯收入，单位GDP能耗，城市化率，以上指标的数据来自《中国统计年鉴》；工业电力消费总量，建筑业电力消费总量，交通运输仓储和邮政业电力消费总量，批发零售业和住宿餐饮业电力消费总量，居民生活用电量，水电生产电力量，火电生产电力量，核电生产量，其他电力生产量，数据来自《中国能源统计年鉴》；研究与发展经费支出的数据来自《中国科技统计年鉴》。

2.2 因子分析

本文使用 SPSS Statistcs进行因子分析。依据因素的内涵及其相关性，并综合前人的研究，将影响电力需求的因素划分为以下几类：宏观经济发展水平、产业电力消费结构、主要行业电力消费结构、人民生活水平、电力生产结构、社会因素。本文以表1显示的宏观经济发展的因子分析为例，对因子分析结果进行说明。

在因子分析时，当KMO值大于0.7且Bartlett 的球形度检验的显著性水平小于0.01时，则原有变量适合因子分析，累积解释的总方差大于80%时，说明因素提取效果良好。由表1到表6的结果可以得出：KMO值均在0.7以上，Bartlett 的球形度检验的显著性水平也均满足要求，累积解释的总方差基本均大于80%或略低于80%，基本符合研究需要，说明六类影响因素的筛选符合要求。

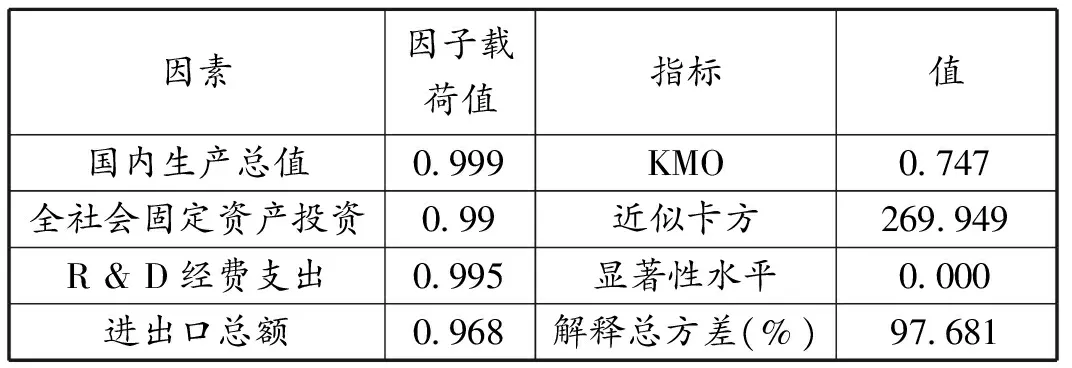
表1 宏观经济发展水平的因子分析

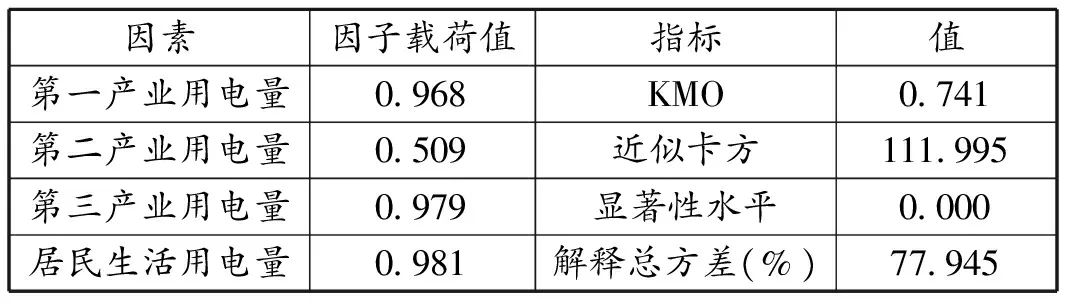
表2 产业电力消费结构的因子分析

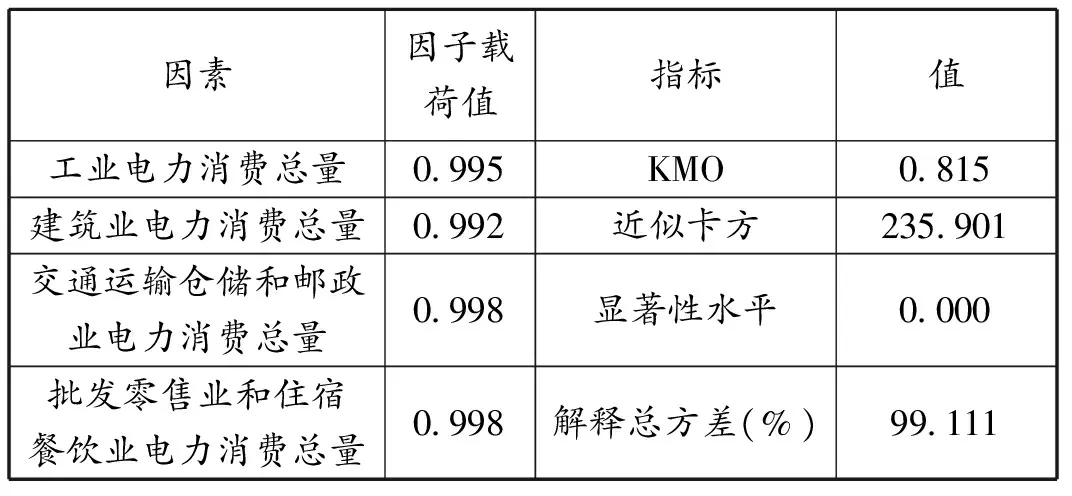
表3 主要行业电力消费结构的因子分析

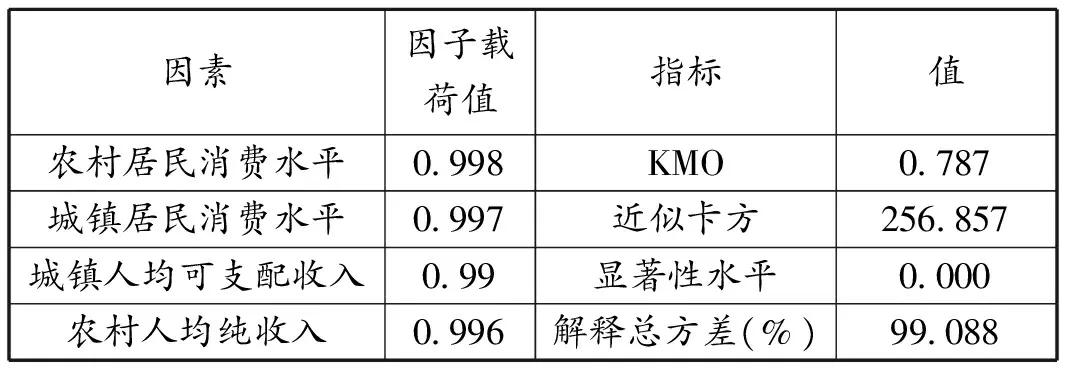
表4 人民生活水平的因子分析

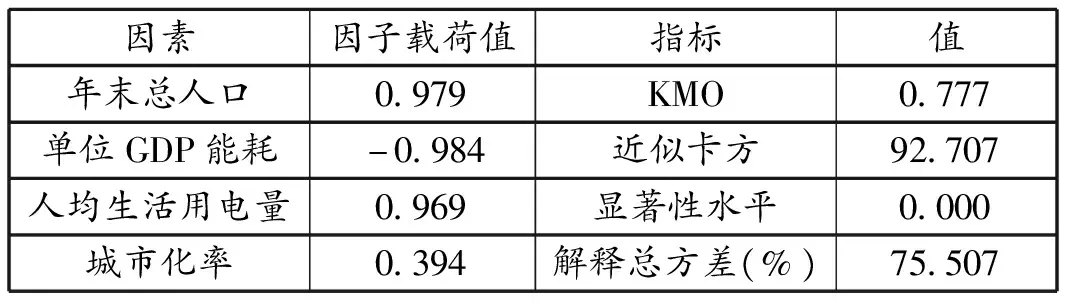
表5 社会因素的因子分析

表6 电力生产结构的因子分析

2.3 实证分析

将因子分析提取的因素作为输入变量，使用1995-2012年的数据作为训练数据，2013-2015年的数据作为预测数据分别使用粒子群优化极限学习机与极限学习机、反向传播神经网络预测，结果如图2所示。

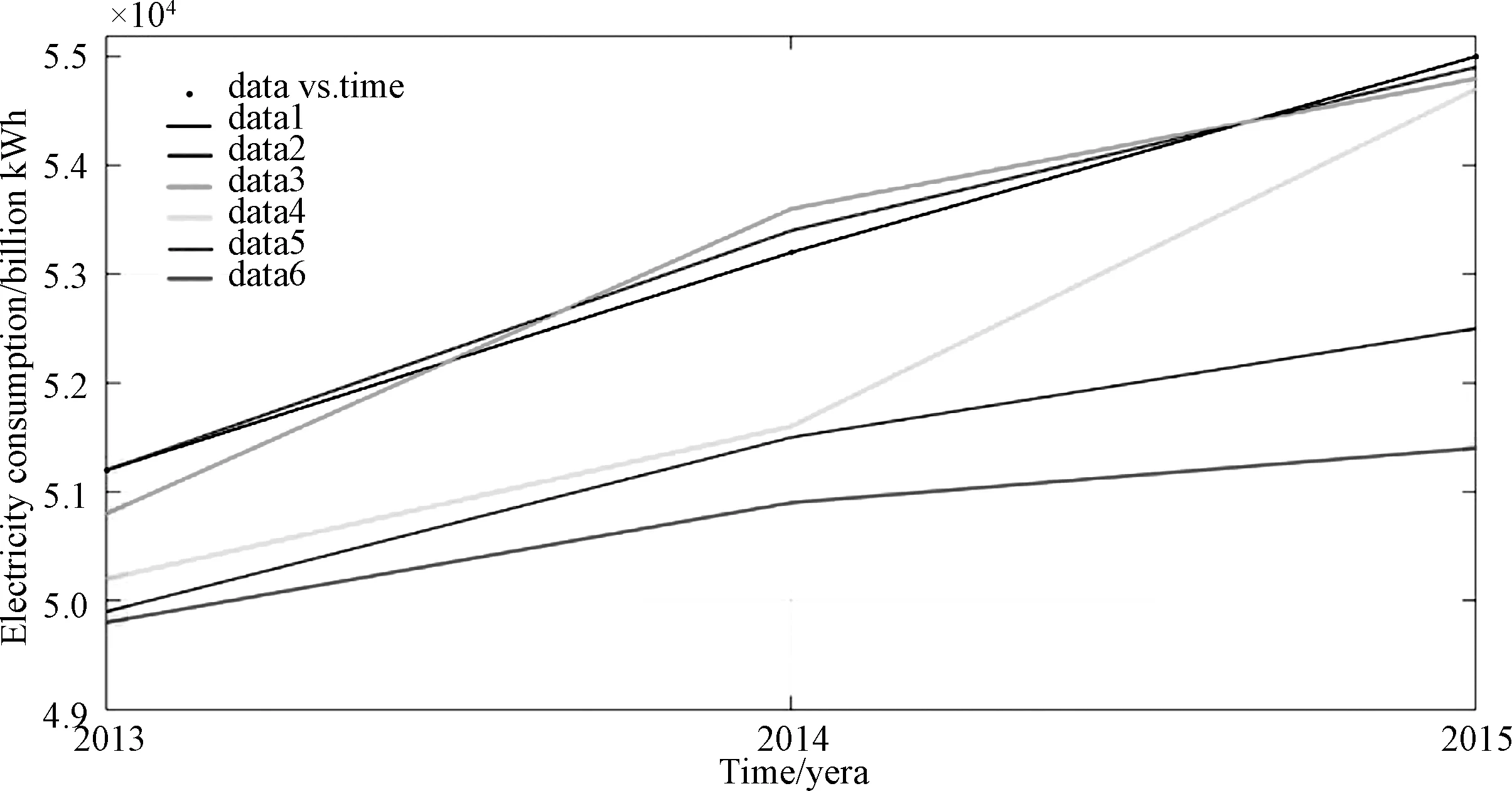
图2 模型预测结果对比

在图2中，data1代表实际值，data2～data6分别代表BP、ELM、CV-LSSVM、DE-SVR和PSO-ELM的预测结果。如图2所示，单纯的ELM预测结果已经优于CV-LSSVM和BP，但相对于DE-SVR较差。而相对于DE-SVR，优化后的PSO-ELM在三个历史负荷上均更接近实际值。

2.4 模型性能评价标准

为了检验某个预测模型相对其他模型的优越性，预测模型的性能通常采用以下几个统计标准进行评价：均方根误差(RMSE)、平均绝对百分误差(MAPE)和平均绝对误差(MAE)。三个指标的数值越小，则说明对应预测模型的性能越好。

在本文中，改进的粒子群算法用于优化极限学习机的输出权值矩阵。在粒子群算法中，最大迭代次数为100，种群大小为40，同时，在极限学习机中隐含层节点为2，其他参数设置如表7所示。

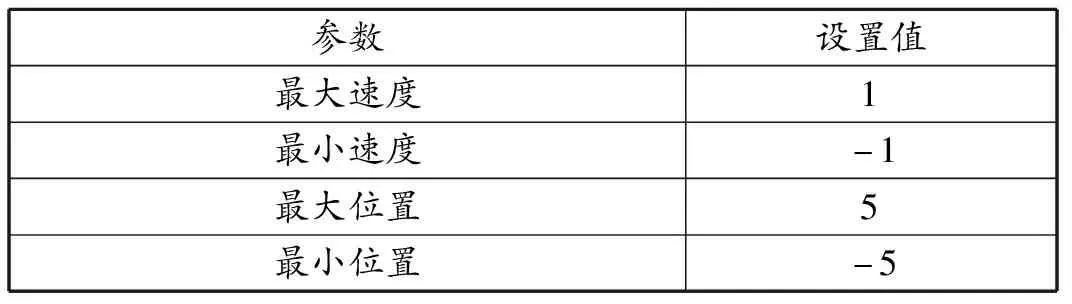
表7 粒子群速度和位置的相关参数

2.5 结果分析

为了验证模型的有效性，除了采用粒子群优化极限学习机(PSO-ELM)进行需求预测外，还引入了差分进化优化的支持向量机(DE-SVR)、交叉验证优化的最小二乘支持向量机(CV-LSSVM)、极限学习机(ELM)和反向传播神经网络(BP)作为对比模型，因此，本文除了可以进行未优化模型以及优化模型的各自横向对比外，还可以进行未优化模型和优化模型之间的纵向对比，以较为全面的对比展示粒子群优化极限学习机(PSO-ELM)在电力需求预测方面的合理性和有效性。误差指标如表8所示。

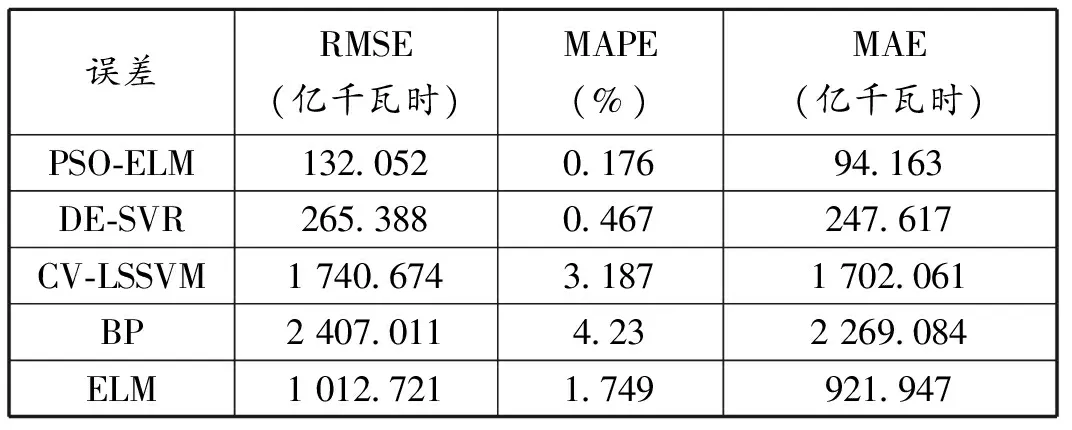
表8 各模型误差对比

如表8所示，2013年到2015年的拟合曲线表明，粒子群优化极限学习机在全国的电力需求预测方面优于其他对比模型，在三个误差指标方面均表现出了显著的优良特性，在电力需求预测方面展现出了良好的适应性。

具体而言，ELM相对于CV-LSSVM和BP表现更好，RMSE、MAPE和MAE均相对最小，尤其在MAE指标方面，ELM分别提高了45.83%和59.37%，但相对于DE-SVR，ELM的三个误差指标均处于劣势，说明单一的ELM虽然预测能力较好，但仍有待改进；而本文中采用的PSO-ELM模型，在三个误差指标上均表现出了最优的性能，其RMSE、MAPE和MAE分别只有132.052 2、0.1757%和94.163 3，且相对于DE-SVR模型分别提高了50.24%、62.38%和61.97%，说明了ELM在利用粒子群算法优化后的良好性能。

综上所述，从误差指标分析可知，良好的预测精度不仅说明了利用因子分析进行数据降维的有效性，而且预测精度的提升也表明了本文中采用的PSO-ELM模型在电力负荷预测中具有的良好前景。

3 结论与展望

3.1 结论

在本文中，选取了6大类共24个指标作为我国电力需求的影响因素，通过因子分析最终筛选出6个变量作为预测模型的输入变量，代入粒子群优化极限学习机模型来预测我国电力需求。最后，通过对比模型的分析，可以得出以下结论：①对影响电力需求因素进行因子分析有助于消除影响因素的多重共线性，提高预测精度，同时也减少了数据维度，降低了计算的复杂性；②在未优化预测模型中，极限学习机相对于反向传播神经网络表现出一定优势；③在优化后的预测模型中，粒子群优化极限学习机在三个误差指标均表现出最好的预测精度，而且需要的隐含层节点数较少，在电力负荷预测中具有明显优势。

3.2 展望

本文运用粒子群优化极限学习机取得了良好的预测效果，但是，也要尝试用更好的算法优化极限学习机以提高预测的精度；在未来的研究中也要考虑影响因素的变化情况，使其更好的表征经济状况，使预测更科学有效。