改进萤火虫算法在地区水资源优化配置中应用研究

2020-07-01贺建文

水利规划与设计 2020年7期

贺建文

(新疆水利厅水资源规划研究所，新疆乌鲁木齐 830000)

水资源是重要经济发展推动力[1- 3]，考虑水资源高效利用是许多水利工程师一直思考的重要研究课题，而研究水资源优化配置一个重要手段即是利用水资源配置模型，通过多目标效益的模型函数求解，进而获得水资源优化配置最佳结果[4- 7]。由于水资源优化配置模型的复杂性，故求解模型采用传统方法一般不能得到最优解，故引入智能算法开展模型求解是当前水资源优化配置课题方面的重要举措[8- 10]。已有一些学者与水利工程师基于水资源配置的多目标特点，通过粒子群算法、模拟人机算法等式求解特定的水资源配置模型[11- 13]。由于不同地区差异性较大，用水与需水单位的不同，模型求解不能照搬以往经验，应根据实地水资源具体供需情况，多方面比较最佳求解方法，进而获得地区内最佳水资源优化配置结果。

1 工程概况

1.1 地质概况

研究区域位于华北平原，区域内河流长度290km，地下水资源超过14000万m3，主要分布在地下岩溶层与基岩裂隙中，年平均可用水资源总量超过26000万m3。另根据工程水文地质踏勘表明，区域内含水层分布在二叠、三叠系中风化砂岩中，降雨补给主要分布在覆盖层孔隙中，但在覆盖层边缘界面与基岩层接触带上有地下水侵蚀破坏现象，孔隙地下水经调查统计分布面积有190km2，踏勘发现区域内岩溶发育，溶洞内含有地下水补充源，并夹有灰质白云岩碎屑，发育碳酸岩类，溶蚀现象显著，为地下水运输转移提供重要渠道。另在山地丘陵地带由于断层地垄等活动，分布有49km2面积，此类地形的存在，帮助补给地下水，提升农业灌溉能力。

1.2 水资源开发现状

本文以2015年为开发现状年份展开分析，经地区内水系调查分析，可供水资源调度分为三个方面：地表水、地下水、雨水集蓄。地表水资源包括有水库等人工蓄水枢纽工程及引渠工程，经调查得知地区内兴利水库库容总计为23万m3，可供水资源为34万m3，其他池坝等蓄水设施可供水资源37万m3，引渠工程主要为小型自建水渠与部分提水工程，共有400处水渠工程与25处提水泵站，共可供应水资源605.2万m3。地下水资源前述分析已知分布在岩溶层中，可供水资源2150万m3。雨水集蓄年均可供应水资源约为47万m3.综上调查统计所述，地区内水资源可供应总量约为2877万m3，其中以地下水资源供应为主，地表水与其他集水工程为辅。

结合地区经济公报与全年经济发展预估值，预计匹配地区工农业发展需要水资源3700万m3，其中农业占比为24%，生活必须水资源占比为24%，为保证生态系统平衡亦需供应5%水资源，剩下的即为工业时代经济发展与第三产业所需。对比地区内可供调度水资源与所需水资源，缺口达823万m3，缺水率22.2%，城市缺水率等级划分见表1，由表1可知，该地区缺水等级属Ⅲ级中度缺水状态，水资源供应较困难，部分地区水资源需考虑人工输送。考虑地区内水资源现状条件以及长期水资源开发所面临的问题，例如水资源分布不均以及用水结构不均衡等问题，急需针对地区内水资源配置规划开展优化分析。

表1 城市缺水率等级划分

2 水资源优化配置模型

2.1 配置模型

为了更好模拟实际用水配置，综合多方面因素考虑，以保障地区经济民生发展经济目标、水资源优化配置彰显社会价值目标、平衡生态及可持续发展生态目标三个方面开展分析。

(1)经济目标函数包括有供水对经济发展带来的效益、供水自身所产生的经济收入、不同需水单位所缴纳费用量级与供水优先级，可用下式表述：

(1)

(2)社会价值目标主要针对于供水调度有助于降低工农业发展受水资源限制约束影响，缓和供需矛盾，稳定经济与民心，故社会价值目标设定为缺水量的函数目标，以下式表述：

(2)

(3)生态目标指尽可能在保障经济发展基础上，生态系统是可平衡状态，且区域内污染物检测浓度符合人类生存安全，故生态目标函数以化学需氧量作为函数表达主体，如下式所示：

(3)

区域内水资源配置函数存在边界约束限制条件，本文以区域需水约束、供水约束、规划配置决策条件约束三个方面开展分析。

需水约束边界条件用下式表示：

(4)

供水约束条件式为

(5)

规划配置决策条件约束式为

(6)

由于水资源配置模型函数考虑多方面因素，实质上是多目标函数，而求解多目标函数需考虑目标量间的互相关系，鉴于此本文设定目标函数间呈线性关系，以此将多目标函数转变成单目标模型，并以目标量值的极大、极小值作为分析变量，得到下式[14]

(7)

式中，F(x)—综合权益；wm—第m个组合权益系数。

衡量经济目标、社会价值目标、生态目标的具体量级可将目标划分成多个二级指标、三级指标，进而给三级指标划分出权重，再获得二级指标权重值，最后得到总评价量级，此实质上是层次分析法的变异理论[15]。各个指标组合成上一级大指标，组合式为

(8)

式中，am、bm—层次分析法分配权重值。

2.2 改进萤火虫算法

2.2.1传统萤火虫算法

智能优化算法有助于提升求解精度，并提高求解速度，本文将在传统萤火虫算法基础上改进，用于求解水资源配置模型。萤火虫算法设定每只萤火虫位置关系均以向量xi表述，其发光亮度与该只萤火虫距离d萤火虫群体有关，萤火虫亮度可表述为

(9)

式中，γ—光吸收系数；rij—位置距离函数关系。

萤火虫相互之间关系式又可表述为

(10)

式中，β0—最大吸引力。

萤火虫个体与群体之间距离关系发生改变，每次位置变化可用下式表述

(11)

式中，t—迭代次数；α—计算步长；rand—随机数。

萤火虫算法计算流程如图1所示。

图1 萤火虫算法计算流程

2.2.2改进萤火虫算法

传统萤火虫算法由于后期收敛性能欠佳，个体萤火虫与群体之间距离关系把握度较差，造成一定迭代误差，本文针对此进行改进，考虑分别以步长、权重值、影响因子为改进对象，最后综合对比出适合本工程水资源优化配置模型计算的改进方法。

(1)改进后计算间隔步长式为

αt+1=αt(1-Δ)

(12)

式中，αt—迭代步长；Δ—变化量。

步长改进可提升迭代次数增长下精度特性，获得的解也更趋于最优，单个萤火虫位置按照如下变化:

(13)

(2)与改进计算步长类似，引入权重值改进重分配，获得下式:

(14)

改变权重值，可以缩小单个萤火虫与群体之间的距离差异性，避免计算过程中处于离散性，则改进后单个萤火虫位置变为[16]

(15)

(3)在改变权重值分配基础上，引入压缩因子概念[17]，直接对萤火虫位置关系进行修正，获得修正后萤火虫位置表达式为

(16)

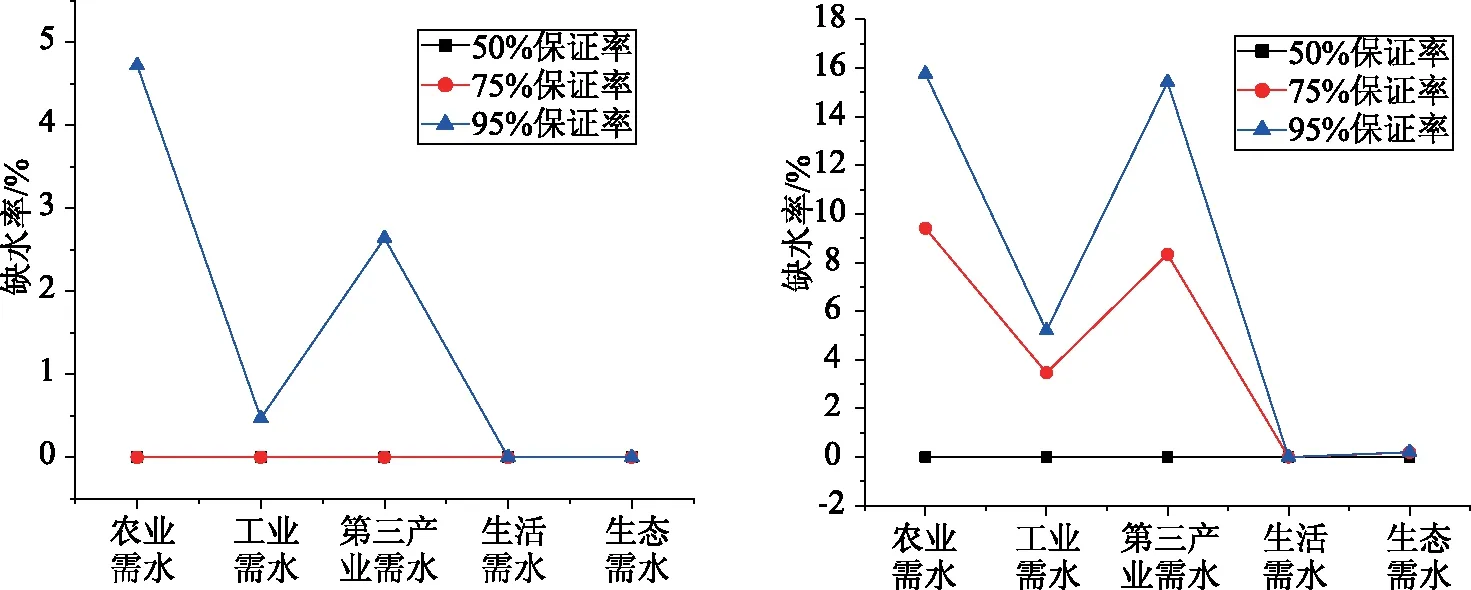
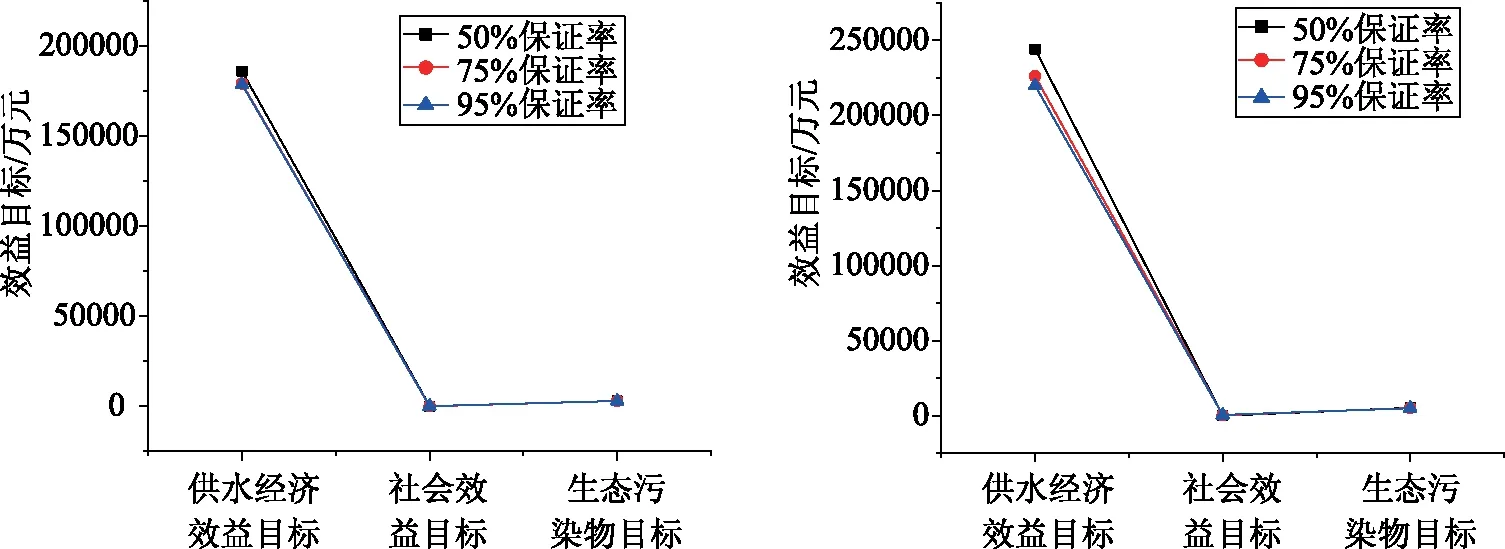
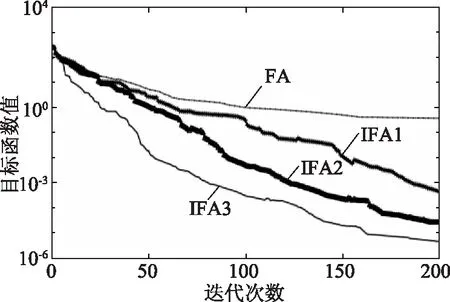
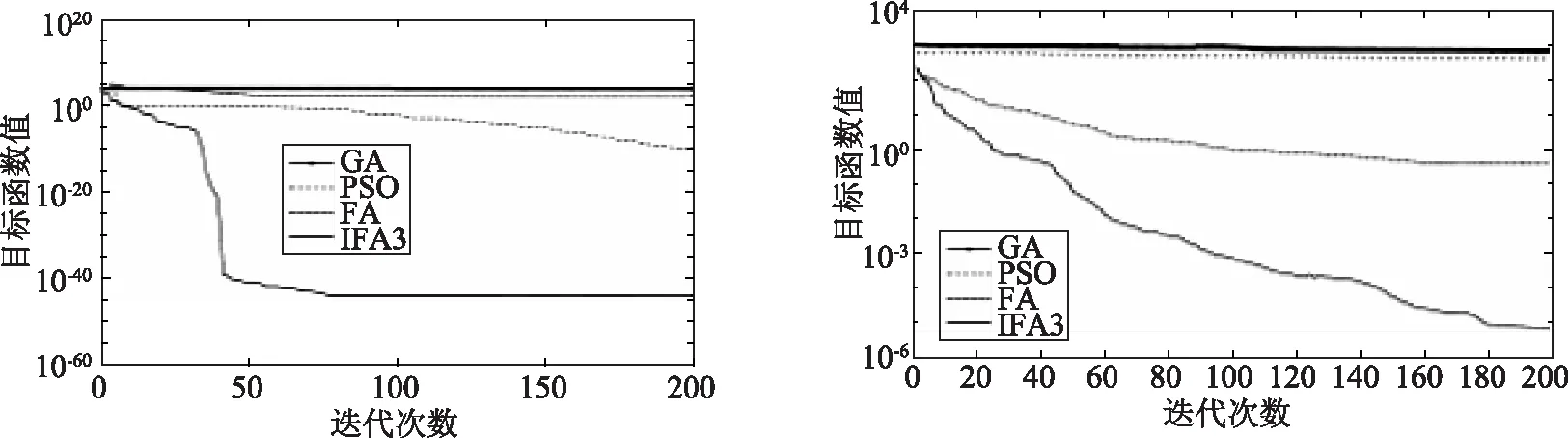
式中，0

针对上述三种改进方法，引入Ackley函数式(17)与其三维图像，如图2所示。

(17)

图2 Ackley函数

分别以上述三种改进萤火虫算法依次迭代计算Ackley函数，三种改进方法分别命名为IFA1、2、3，传统萤火虫算法为FA，即获得目标函数解与迭代次数关系如图3所示，从图中可看出，第三种改进萤火虫算法计算迭代速度最快，其精度亦是最高。

图3 目标函数-迭代次数精度图

为保证所用测试目标函数求解结果的个体性，本文再引入另外两个Sphere、Rastrigin函数，式(18)—(19)及图4所示，以第三个改进萤火虫算法IFA3、FA算法、GA算法、PSO算法开展求解精度对比分析，获得图5所示结果。

Sphere函数

(18)

Rastrigin函数

(19)

不同算法求解目标函数下的精度图如图5所示，从图5中可看出，Sphere、Rastrigin函数求解精度最高均为改进萤火虫算法IFA3，收敛速度也是最快。综上前述对比分析，表明使用第三种改进方式获得萤火虫算法优于其他算法求解，本文将利用该种方式改良萤火虫算法求解水资源优化配置模型。

3 模型计算结果分析

在上述分析基础上，获得该地区内水资源在2025、2035水平年水资源优化配置结果，如图6所示。从图6中可看出，在水平年2025，50%保证率条件下农业需水总量为1109.5万m3，而在75%保证率条件下，农业需水总量增大了5.5%，达1171.87万m3。工业需水总量、第三产业需水量、生活需水、生态需水四个用水项目在保证率变化条件下，未发生较大改变。2030水平年中，除生活需水与生态需水稳定不变，其他需水量单位有微许下降波动。

从缺水率分布(如图7所示)看，水平年2025年随保证率增大到接近100%，除生活需水与生态需水外，其他几个需水项目量均出现一定程度缺水量，其中以农业需水的缺水率最大，达4.72%。当水平年推移至2035年时，在保证率75%时即已在各需水项目中产生缺水，当保证率增大至95%时，农业需水与第三产业需水项目的缺水率已超过15%。图7中还可看出，两个水平年不论保证率多高，生活需水总是供需平衡，缺水率一直为0。综上分析表明，保证率增大，一定程度会造成部分用水项目出现缺水，当水平年延后，缺水项目增多，且缺水率增大。

图4 Sphere、Rastrigin函数三维图

图5 Sphere、Rastrigin函数-迭代次数精度图

图6 水平年2025、2035水资源优化配置结果

所计算出的模型综合效益目标曲线如图8所示，从图8中可看出，水平年2025年供水经济效益目标随保证率增大在逐渐减小，社会效益目标在增大(从0增大至70.8万m3)，生态污染物目标价值在减小，从50%保证率增大至95%时，生态目标效益(化学需氧量)减小了0.5%。分析表明，由该多目标函数求解该地区水资源配置后，整体上在高保证率时，虽出现供水缺口，但生态目标并未出现缺口，而是呈现化学需氧量(污染物)浓度的降低。