基于模拟退火算法的电源规划
2020-07-01韩晓辉
韩晓辉, 高 远, 颜 丽, 米 阳
(1.中国电力工程顾问集团 华东电力设计院有限公司, 上海 200063; 2.上海电力大学, 上海 200090)
传统的电力系统规划已经不能满足当今社会经济快速发展的要求,因此必须对其进行不断改进和完善[1]。合理的电力系统规划有助于确定电力设备增装的时间、地点和类型等,从而满足规划年限内的电力需求,并在符合电力系统技术性指标(如20%备用,N-1准则,可靠性等)的前提下,使规划电力系统的总费用(包括投资费用、运行费用、停电费用等)最小。按照规划对象的不同,电力系统规划可分为电源规划、输电网规划和配电网规划等。
由于电力系统的外部环境不断变化,酸雨和温室效应等环保问题日益突出,电源规划也会受到这些因素的影响。因此,电源规划不仅要考虑经济性问题,还包括可靠性、环保性等诸多因素。其目标函数也涉及多个方面,对于多目标电源规划的目标函数也应包容各种评价因素[2]。
目前,遗传算法[3-8]在电源规划问题中被广泛运用,是一种模仿生物进化过程的随机方法。遗传算法包括选择、交叉、变异3个基本操作,在处理一些多目标、非线性函数优化问题时可以得到较好的结果,但实现过程较为复杂。此外,粒子群算法[9-10]、免疫算法[11]、蚁群算法[12]、0-1规划[13]等算法在电源规划问题中也被经常使用。其中,粒子群算法源于对鸟群捕食的行为研究,是一种基于迭代的优化工具,与遗传算法类似,但没有交叉和变异的环节,而是通过在解空间跟踪最优粒子进行搜索。
本文利用模拟退火算法和等微增率模型[14-15]对优化目标进行合理探讨和求解。模拟退火算法是一种基于蒙特卡洛思想设计的近似求解最优化问题的方法,算法思想源于对固体物质退火的模拟。该算法以一定的概率来接受一个比当前解要差的解,因此有可能会跳出这个局部的最优解,达到全局的最优解。此外,为了取得经济上的正确评价,本文将不同时刻的资金折算为同一时刻的资金,然后在相同的时间基础上进行比较,并引入了等年值[16]的概念。
1 工程经济性分析
在不同时刻投建发电机组所需的成本和获得的利润会有所不同,其价值也不相同。为了取得对电力系统规划经济性的正确评价,应该将不同时刻的资金折算为同一时刻的资金,并在相同的时间基础上进行比较。假设P表示一笔资金的当前等效金额(现值),F为未来第t年的等效金额(将来值),A为分摊到每一年的等效金额(等年值)。
资金现值、将来值和等年值的关系式分别为
F=P(1+r)t
(1)
(2)
(3)
式中:r——贴现率;
N——机组的使用寿命或规划年限;
R——资金回收系数。
当R用于折算机组投资成本时,N表示机组使用寿命,P表示机组投资成本现值;当R用于折算运行成本时,N表示规划年限T,P表示T年内的运行总成本。
对发输电可靠性测试系统(Institute of Electrical and Electronics Engineers-Request to Send,IEEE-RTS),若在未来10年内增装10台机组,现有以下3种投资方案。
第1种投资方案是在第一年投建全部机组,则机组的投资成本现值为
P=10P1
(4)
第2种投资方案是在每一年投建1台,第1年的现值为P1,第2年的现值为P1/(1+r),以后每一年的资金现值成等比关系,可得
(5)
第3种投资方案是分别在第一年和最后一年投建5台,可得
(6)
将式(4)~式(6)代入到式(1)~式(3)中,对求解得出的值进行比较。结果越小,方案越优。在所有结果中,方案2的等年值最小,即该投资方案为最优。
2 IEEERTS单阶段电源扩展规划
某电力公司的IEEE-RTS系统由32台发电机组构成,总装机容量为3 405 MW,峰值负荷为2 850 MW。以2019年为基准年,假设2030年系统峰值负荷增长30%,规划2030年当年增装机组的类型和数量。不考虑机组运行费用和系统停电损失费用。
该系统原有机组和待增装机组的电气参数、经济性参数分别如表1和表2所示。

表1 IEEERTS系统已有发电机组参数

表2 IEEERTS系统待增装发电机组参数
2.1 数学模型的建立
假设规划年限为T年,Xt表示规划年t增装的各类型机组,Y表示现有系统中的机组,则电源规划模型的目标函数为
(7)
式中:CIt——机组的等年值投资成本;
COt——电厂运行成本;
CLt——停电损失费用(成本)。
电厂运行成本为
(8)
式中:Pitτ——第i台机组在t年τ时刻的输出功率。
系统待装机组有4种类型。以2019年为基准年,至2030年结束,总共11年。假设mij为第i年第j种类型机组的数量(i=1,2,3,…,11;j=1,2,3,4),可以得出多项式
(9)
由上可得
(10)
可得目标函数为
(11)
约束条件如下
(12)
式中:L′——2030年发电容量;

L——2019年发电容量。
2.2 模拟退火算法概述
模拟退火算法最早由METROPOLIS N提出,1983年KIRKPATRICK S等人将模拟退火的思想成功引入组合优化领域。目前,模拟退火算法已经应用于各门学科,以解决非线性系统的优化问题。理论上已经证明,模拟退火算法是一个全局最优算法,而且概率为1接近最优值,克服了对初值的依赖。算法的基础源于对固体退火过程的模拟,采用Metropolis准则,用冷却进度表控制算法进程,最终得到一个近似最优解。固体退火是指将固体加热到足够高的温度后,使分子呈随机排列状态,然后逐步降温使之冷却,最后分子以低能状态排列,固体达到某种稳定状态。热力学中的退火现象是指物体逐渐降温时发生的物理现象。温度越低,物体的能量状态也越低,到达足够的低点时,液体开始冷凝与结晶,在结晶状态时,系统能量状态最低。
物理退火过程中,在温度Tc,分子停留在状态S满足Boltzmann概率分布
(13)
E(S)——状态S的能量;
kB——Boltzmann常数,kB>0。
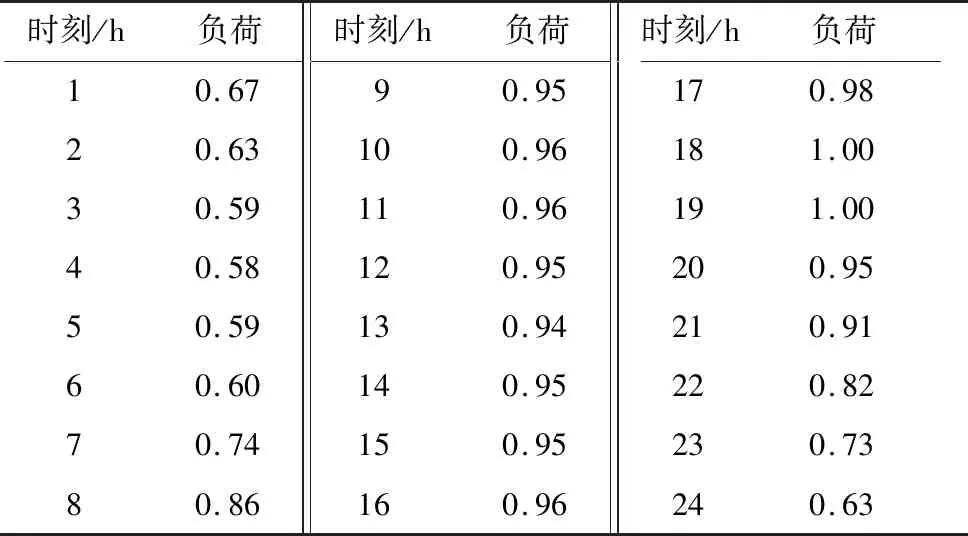
在同一温度下,选定两个能量值E1 (14) 模拟退火算法的基本思想是:在一定的温度下,搜素从一个状态随机地变化到另一个状态,随着温度的不断下降直到最低温度,搜索过程以概率1停留在最优解。根据玻尔兹曼概率分布可以得出:在同一个温度,分子停留在能量小状态的概率大于停留在能量大状态的概率;温度越高,不同能量状态对应的概率相差越小;温度足够高时,各状态对应的概率基本相同;随着温度的下降,能量最低状态对应的概率越来越大;温度趋于零时,其状态趋于1。 模拟退火算法的基本流程如下。 (1) 随机产生一个初始解x0,令xbest=x0,并计算目标函数数值E(x0);k=0;t0=tmax。 (2) 若在该温度下达到内循环,则停止循环。 (3) 否则,从当前最优解xbest的邻域N(xbest)中随机选一xnew,计算新的目标函数值E(xnew),并计算目标函数值的增量ΔE=E(xnew)-E(xbest):若ΔE<0,则xbest=xnew;若ΔE>0,且exp(-ΔE/t)>random(0,1)时,xbest=xnew。 (4)tk+1=update(tk),k=k+1:若满足停止条件,则终止计算,输出最优解;否则,回到第2步。 结合上述数学模型的相关参数,利用MATLAB软件求解,得出从2020—2030年4种新型机组每年新增的数量为:2030年增建1号新型机组1台,2号新型机组2台,3号新型机组2台,4号新型机组0台。当需要增建新型机组时,年份越靠后,所需费用相对越少。 系统典型日负荷(标幺值)信息如表3所示。其中峰值负荷为2 850 MW。 表3 系统典型日负荷 考虑典型日第12 h和第24 h现有系统各机组的最优负荷分配方案,不考虑机组启停和爬坡率限制。 对现有的32台机组进行负荷分配,使得机组的总运行费用最少。这个问题的目标函数及其约束条件为 (15) 式中:Piτ——机组i在τ时刻输出的有功功率; ατ——τ时刻相对于峰值负荷的标幺值; PL——2019年峰值负荷量; Pi,min,Pi,max——输出功率的最小值和最大值。 为了求解这一问题,需要运用等微增率法进行机组负荷分配。下面先对等微增率方程进行推导。 设第i台机组τ时刻运行费用为COiτ,则 (16) 32台机组τ时刻的运行费用为 (17) 系统负荷的平衡条件为 (18) 为求得在负荷平衡条件下目标函数的极小值,引入一个拉格朗日乘子λ,构造拉格朗函数为 (19) 除了各机组的有功出力外,函数La中还包含了独立变量λ,从而将原来的条件极值问题转换为求拉格朗日函数的无条件极值问题。当拉格朗日函数对全部变量的偏导等于零时,才能够取得极值,即 i=1,2,3,…,32 (20) (21) 由于机组的出力限制,并不是在所有条件下都可以按等微增率原则来分配机组或发电厂间的负荷,有一些条件并不适用。比如,当某些机组或发电厂的分配功率没有达到最小出力或超过最大出力范围时,等微增率原则被破坏。因此,在建立机组负荷最优分配问题数学模型时,必须考虑机组的出力上下限,在数学模型中将其作为机组负荷优化问题的约束条件,即增加不等式约束条件 Pi,min≤Piτ≤Pi,max (22) 当出力的计算值Piτ低于最小值或者高于最大值时,将等微增率与TUCKER K提出的最优条件结合使用。也就是说,依据等微增率原则在符合系统功率的一系列需求约束条件下分配负荷后:当Piτ 等微增率法的实现过程为 (23) 故可得 (24) 第τ小时中,32台机组的运行总成本为 (25) 设第τ小时中,32台机组输出的总功率为Pτ,则有 (26) 故目标函数为 (27) 约束条件有以下两个。 (1) 第τ小时中输出的总功率需要满足系统典型日在第τ小时所需的负荷。假设在典型日第τ小时所需的负荷相对于峰值负荷的标幺值为ατ,则 Pτ≥ατPL (28) (2) 每台机组都有各自的机组容量和最小机组出力,且当机组不工作时,其输出功率为零,则 Piτ∈{0}∪{Piτ|Pi,min≤Piτ≤Pi,max} (29) 结合已给出的相关数据,利用等微增量法求得现有系统各机组在典型日第12 h的最优负荷分配方案,如表4所示。 由表4可以看出,部分机组的输出功率超出了约束条件,故不能使用等微增量法。 利用模拟退火法结合MATLAB软件,求解现有系统各机组在典型日第12 h和第24 h的最优负荷分配方案,如表5所示。限于篇幅,仅列出部分结果。 由表5可以看出,要使得运行成本最低,并不是所有机组都必须工作。通过计算和比较可以得到,方案1和方案5分别为第12 h和第24 h各机组的最优负荷分配方案。 表4 利用等微增量法求得的各机组在典型日第12 h的最优负荷分配方案 表5 利用模拟退火算法求得的各机组典型日第12 h和第24 h的负荷分配方案 合理的电源规划是电力系统安全、可靠、经济运行的前提和基础。本文利用模拟退火算法,考虑投资成本和运行成本,给出了不同要求下的最优分配方案,体现了模拟退火算法在解决复杂最优规划上的优越性。此模型可推广到更多的最优分配方案,并可以考虑其非线性约束条件,对电源规划做进一步的探讨。拉格朗日乘数法一般用于解决常规的最优化问题,而面对较复杂的多目标、多条件优化问题,模拟退火等启发式算法能够较容易得到较优解。2.3 结果与分析
3 系统典型日负荷电源规划
3.1 数学模型
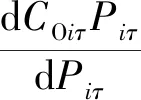
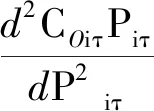
3.2 结果与分析


4 结 语
