基于最优导引律的高空滑翔鱼雷弹道设计

陈嘉杰, 王 中, 曹小娟, 张秦南, 蔡卫军

基于最优导引律的高空滑翔鱼雷弹道设计

陈嘉杰, 王 中, 曹小娟, 张秦南, 蔡卫军

(中国船舶重工集团公司 第705研究所, 陕西 西安, 710077)

高空滑翔鱼雷在打击潜艇的过程中, 采用滑翔增程方式增加攻击范围, 能够在潜艇防区外发起攻击, 可有效提高载机生存能力。其空中弹道主要包括滑翔增程弹道和雷伞弹道, 滑翔增程弹道结束后, 需要进行雷翼分离并进入雷伞弹道, 故其终端弹道约束相比于一般的空投鱼雷更为复杂。文中针对滑翔弹道终端的位置约束和终端弹道倾角约束, 依据最优控制理论, 建立高空滑翔鱼雷弹道模型, 提出了满足终端弹道倾角约束的最优导引律; 根据最优导引律和过载量控制的原理, 给出了滑翔翼的积分过载控制方法; 最后分别针对比例导引律和最优导引律进行弹道仿真对比。仿真结果表明, 采用比例导引律可以满足位置约束(水平控制精度和雷翼分离高度), 但无法控制弹道倾角; 而采用最优导引律则可在实现水平位置控制精度和雷翼分离高度均满足约束的同时实现对弹道倾角的控制。

高空滑翔鱼雷; 弹道最优控制; 比例导引律; 最优导引律

0 引言

反潜作战是各国海军的一项重要任务,在众多的反潜手段中, 航空反潜平台携带空投鱼雷打击潜艇已成为十分有效的反潜手段, 可以说航空平台对潜艇具有“不对称”的优势[1-2]。然而, 这种优势随着潜艇防空技术的发展正在逐渐缩小。传统方式的空投鱼雷技术, 在投放鱼雷前, 航空反潜平台首先需要降低高度和速度, 然后再进行投雷。美国的P-3反潜机在投放鱼雷前, 必须下降到距离海面150 m 左右, 减速后, 再进行鱼雷投放[3]; 俄罗斯的AIIP系列航空反潜武器, 搭载于图-142等飞机, 其投雷高度大约为500~600 m。随着潜艇防空技术的发展, 已有多国潜艇具备隐蔽发射潜空导弹的技术[4], 目前的潜射防空导弹射程已经达到10~15 km, 普通空投鱼雷的高度无法保证航空平台的安全[5]。

考虑到低空反潜安全性的降低, 美国海军带头开启了高空反潜武器的研制[6-7], 其在2006年6月授予洛克希德·马丁公司一份合同, 正式启动“高空反潜武器概念”(high altitude anti-submarine warfare weapon concept, HAAWC)的研制计划[3]。该公司的高空滑翔鱼雷系统由滑翔翼组件和鱼雷组成, 依据滑翔增程原理, 给MK54鱼雷加上其设计的“远程开火”(Longshot)高空滑翔装置, 以达到增加投放高度和射程的目的。相比于一般的空投鱼雷, 可有效提高轻型鱼雷的反潜攻击范围。试验验证了该系统在投放高度为6 km的情况下, 高空反潜武器的射程能够达到33~37 km[7], 较好地降低了航空反潜平台被攻击的危险。

空中滑翔增程弹道极大地扩大了高空滑翔鱼雷的攻击范围, 是高空滑翔鱼雷实现防区外攻击的关键[8]。高空滑翔鱼雷的滑翔增程阶段结束后, 需实现滑翔翼和鱼雷的分离、安全开伞, 然后进入雷伞弹道[9-10]。文中重点研究滑翔增程弹道, 这一段弹道的终点是雷-翼分离点, 其弹道设计需满足位置约束、姿态约束等约束条件, 是一个典型的多约束条件下的弹道导引律求解问题[11]。

在高空滑翔鱼雷导引律方面, 可查阅的资料较少, 但可以借鉴导弹、制导炸弹和火箭助飞鱼雷的相关经验。目前最常见的导引方法是比例导引法与最优导引法。以文献[12]为例, 该文献利用比例导引律, 对火箭助飞鱼雷弹道进行导引, 结果显示, 比例导引对位置导引效果较好, 而对鱼雷姿态无法进行调整。因此, 文中针对滑翔弹道终端的位置约束和弹道倾角约束, 研究最优导引规律, 并通过软件仿真弹道曲线, 验证推算的导引规律是否满足多约束要求, 并与比例导引律的导引效果进行对比。

1 高空滑翔鱼雷的运动描述与弹道倾角约束下的最优导引律推导

1.1 高空滑翔鱼雷数学模型

鱼雷动力学和运动学数学模型为

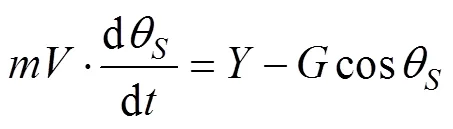
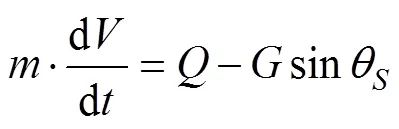
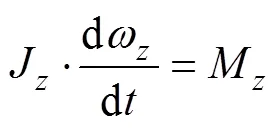
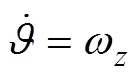
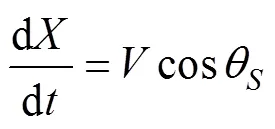
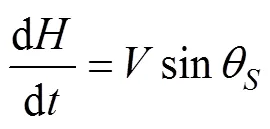
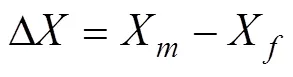
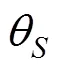
1.2 最优导引律推导

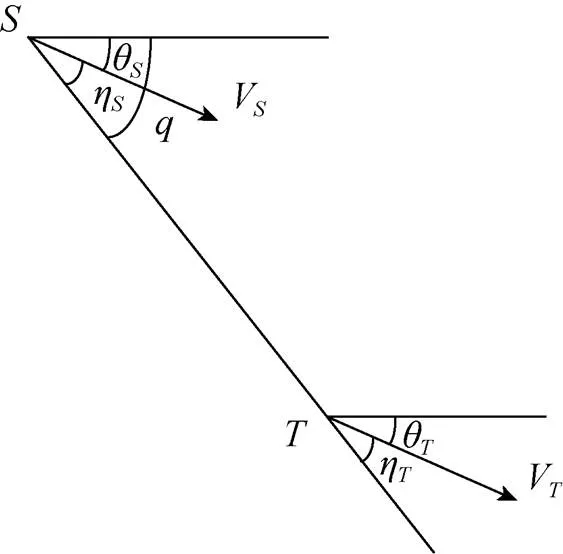
图1 高空滑翔鱼雷与滑翔翼分离点间的相对运动关系

由高空滑翔鱼雷与分离点间的相对运动关系, 可以列出如下相对运动方程

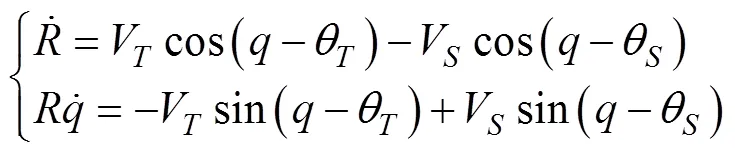
文中研究将滑翔鱼雷投放到固定位置的导引规律, 因此可将方程简化为

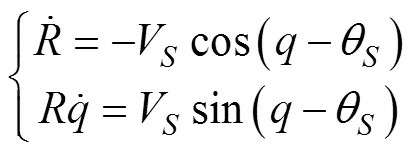
对上式第2项求导, 代入第1项, 进行化简, 得

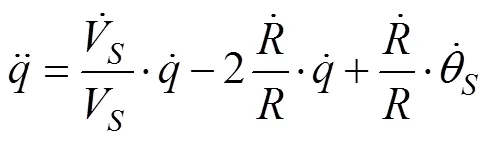
在被动飞行段, 有

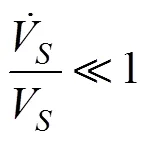
因此可令

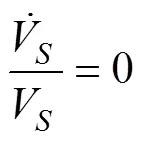
则

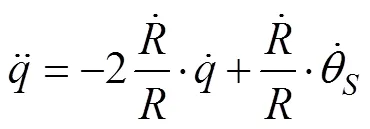
记

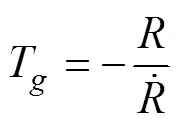
取状态变量和控制变量为

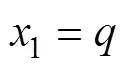
可以将上式改为状态空间方程

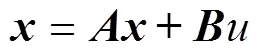
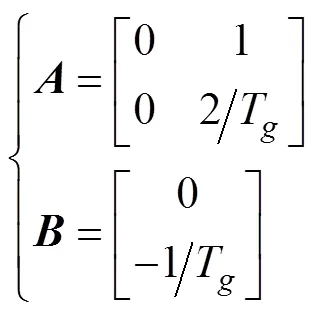
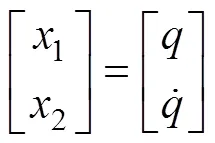
下面用最优导引理论计算导引律, 在这个状态系统中, 期望的终端状态变量为

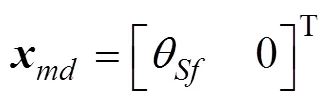
改变状态变量

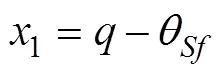
系统状态方程不变, 改变后的期望终端状态变量为

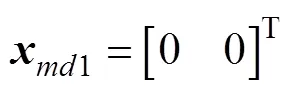
联立式(17)与式(22), 有

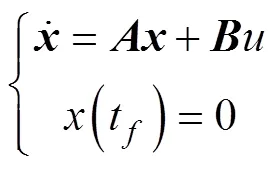
上式为变系数非齐次的线性微分方程组, 文中对高空滑翔鱼雷的弹道倾角作一定的要求, 根据最优控制理论, 选取性能指标如下

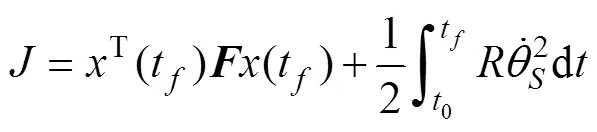
根据文献[13]的求解方法, 可以得到系统的带有二次型性能指标的最优控制为

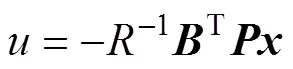
式中,可由逆Ricatti矩阵求解获得。逆Ricatti矩阵为

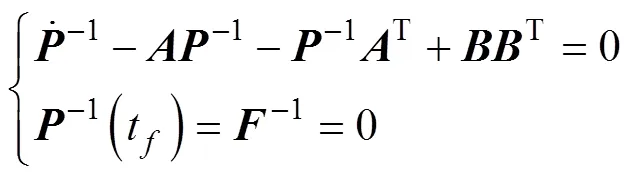
求解上式, 可得

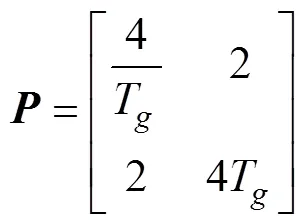
将上式代入到导引律式(25)中, 可得

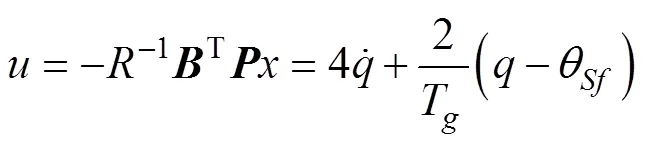
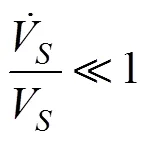
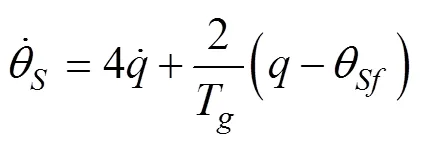
而在工程上, 常用的比例导引律形式为

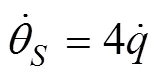
将比例导引律和有弹道倾角约束的最优导引律进行对比可以发现, 最优导引律在形式上, 增加了一项与期望弹道倾角相关的项, 正是因为在建立相对运动模型的过程中考虑了弹道倾角约束, 并将弹道倾角约束体现在了模型中。而导引律中和期望弹道倾角有关的项是最优导引能够对弹道倾角进行约束的关键所在, 在接下来的仿真过程中, 将对此进行验证。

在simulink软件中, 通过仿真比例导引和最优导引在高空滑翔鱼雷被动飞行段的作用情况, 验证2种导引律的导引效果。

1.3 滑翔翼控制规律

高空滑翔鱼雷在滑翔增程段中, 通过改变滑翔机的舵机, 完成对整个滑翔鱼雷的姿态控制。根据设计的导引律, 所采取的控制量为轨道倾角变化率。在实际飞行过程中, 滑翔机控制系统的执行器为滑翔机的舵机, 一般采用过载控制[12], 即将轨道倾角变化率转化为过载指令, 进而控制舵机。比例积分式过载控制方程为

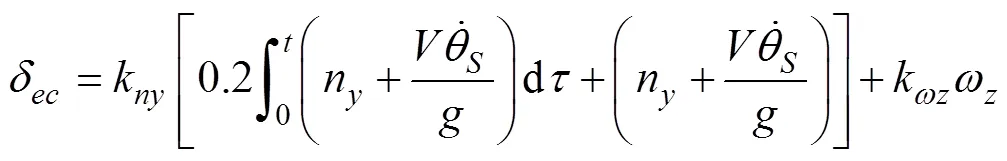
根据高空滑翔鱼雷的运动学和动力学方程, 以及设计的控制系统(见图2), 在simulink中搭建仿真系统进行仿真。

2 仿真结果与分析

2.1 仿真条件

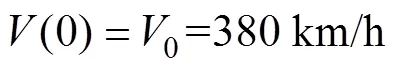
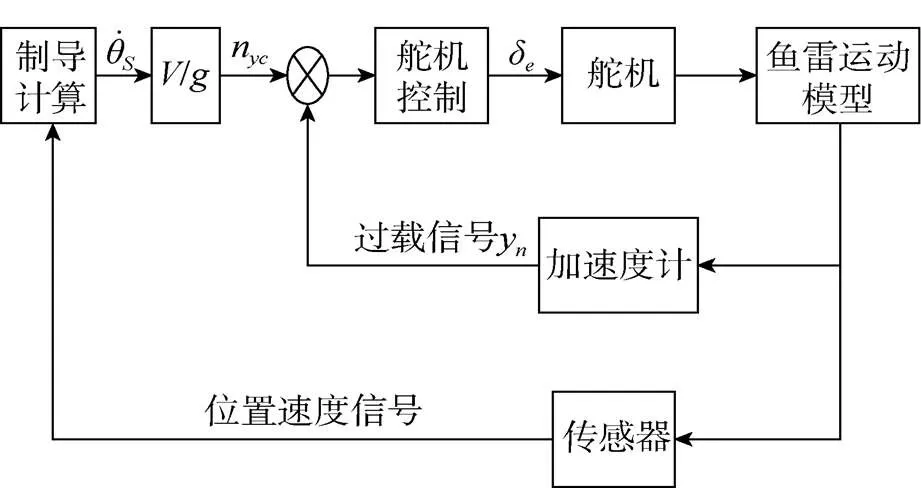
图2 控制系统框图

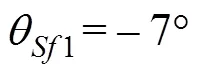
2.2 仿真结果

根据设定的仿真初始条件和终端约束条件, 通过更改制导模块中的参数, 分别对比例导引和最优导引进行仿真, 仿真结果如下。

2.2.1 比例导引律下滑翔鱼雷飞行情况

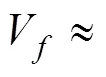
可以看出, 比例导引律可以较好地约束水平位置与雷翼分离高度, 但对弹道倾角无法进行约束。而观察鱼雷攻角变化曲线可知, 高空滑翔鱼雷在开始滑翔阶段后, 迅速形成了一个攻角, 由于存在滑翔翼, 因此在维持一定攻角的情况下, 可以实现滑翔增程, 并完成防区外攻击。

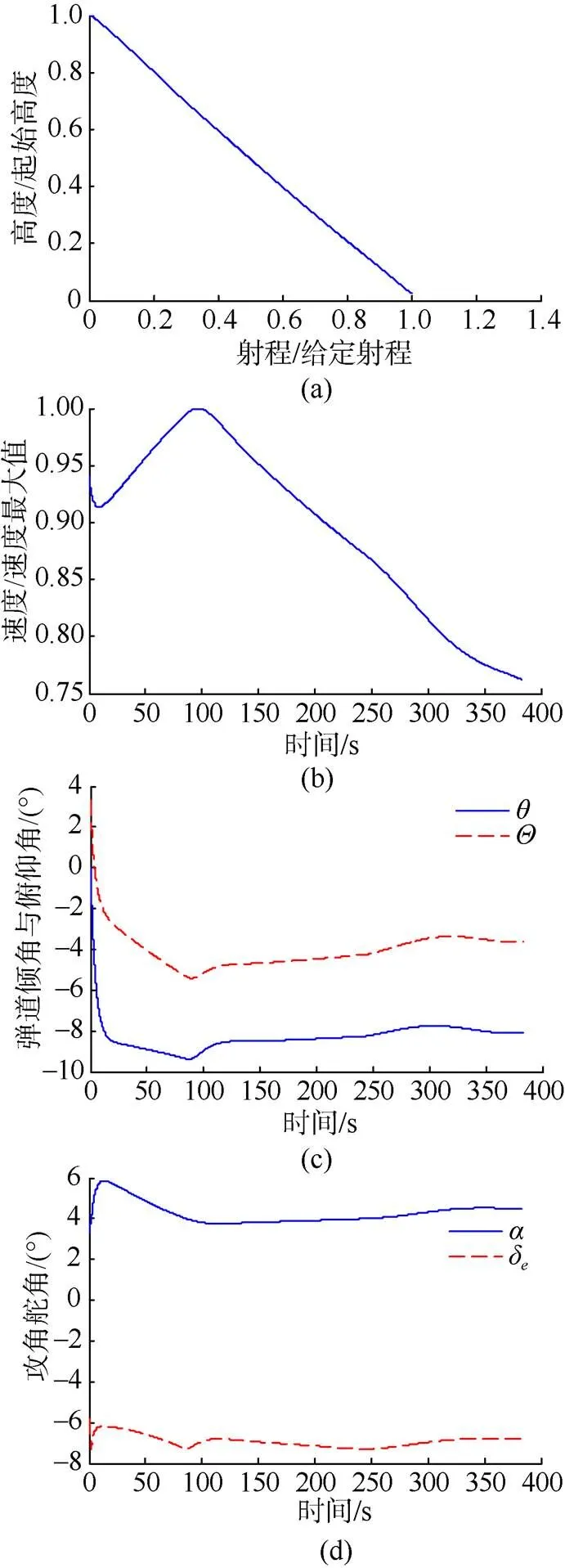
图3 比例导引仿真结果

2.2.2 带弹道倾角约束的最优导引律

可以看出,在最优导引律的作用下, 高空滑翔鱼雷不仅在位置约束(水平位置控制精度和分离高度精度)上能够符合要求, 还能够使鱼雷弹道倾角与期望的终端弹道倾角一致。而观察舵角和攻角变化曲线可以得知, 最优导引律与比例导引律不同的是, 最优导引在滑翔弹道的末段, 通过调整舵角实现了对弹道倾角的控制。

图4 期望的终端弹道倾角为7°时最优导引仿真结果

Fig. 4 Simulation results of optimal guidance as expe- cted terminal trajectory inclination angle is7°

图5 期望的终端弹道倾角为10°时最优导引仿真结果

Fig. 5 Simulation results of optimal guidance as expec- ted terminal trajectory inclination angle is10°

综合最优导引律的2个作用结果可以知道, 最优导引不仅能较好地进行位置约束(水平位置和分离高度), 还能调整终端弹道倾角, 导引效果良好。

3 结论

文中基于比例导引规律和最优控制理论, 综合考虑位置与角度约束, 通过理论分析计算, 给出了一种基于比例导引改进的满足弹道倾角约束的最优控制导引律, 并分别基于比例导引与文中得出的最优导引律进行了数学仿真, 结论如下:

1) 比例导引能够较好地满足位置约束(水平位置控制精度与分离高度), 但是无法对终端弹道倾角进行控制; 最优导引律能够满足终端弹道倾角的约束, 且水平位置控制精度和分离高度精度均能满足要求, 导引效果良好;

2) 比例导引和最优导引均是通过快速确定攻角, 实现滑翔增程, 而最优导引与比例导引的区别在于滑翔弹道的终端, 最优导引律能够通过改变舵角实现对弹道倾角的调整。

文中导引律推导过程中, 在建立模型时考虑到了弹道倾角期望值, 由此推导出的导引律可以对弹道倾角进行约束。在之后多约束导引律的推导过程中, 可以通过合理建立模型, 将不同的约束反映到模型中, 以实现对不同约束的满足。

[1] 杨世兴, 李乃晋, 徐宣智, 等. 空投鱼雷技术[M]. 昆明: 云南科技出版社, 2001.

[2] 王志杰. 研制高空反潜鱼雷的必要性及关键技术[J]. 鱼雷技术, 2009, 17(3): 1-4.Wang Zhi-jie. Necessity and Key Technologies for Deve- loping High Altitude Anti-submarine Torpedo[J]. Torpe- do Technology, 2009, 17(3): 1-4.

[3] 帅智浩, 曹小娟, 王志杰. 鱼雷高空投送载体结构设计特性研究[J]. 鱼雷技术, 2014, 22(4): 241-244, 253.

Shuai Zhi-hao, Cao Xiao-juan, Wang Zhi-jie. Analysis on Structural Design Characteristics of High Altitude Delivery Carrier of Torpedo[J]. Torpedo Technology, 2014, 22(4): 241-244, 253.

[4] 朱清浩, 吴锐, 朱君. 潜射防空导弹发展与应用现状综述[J]. 科技创新导报, 2010(3): 1, 3.

[5] 李伟, 荣海洋, 刘海光. 潜空作战与高空反潜概念武器[J]. 飞航导弹, 2010(6): 33-37.

[6] 潘光, 吴文辉, 毛昭勇, 等. 高空远程滑翔鱼雷全弹道仿真关键技术[J]. 鱼雷技术, 2009, 17(4): 10-15.

Pan Guang, Wu Wen-hui, Mao Zhao-yong, et al. Key Technologies about Complete Trajectory Simulation for High Altitude Long-range Gliding Torpedo[J]. Torpedo Technology, 2009, 17(4): 10-15.

[7] 谢力波, 李瑞红, 程辉辉. 航空反潜的新需求-高空反潜武器[J]. 飞航导弹, 2016(1): 40-43.

[8] 钱东, 孙正杰. 新型空潜攻防武器及其对反潜战的影响[J]. 鱼雷技术, 2008, 16(6): 1-8.Qian Dong, Sun Zheng-jie. Anti-submarine Warfare(ASW) Weapons and Sub-to-air Missile with Influences on Future ASW[J]. Torpedo Technology, 2008, 16(6): 1-8.

[9] 张礴, 宋保维, 王司令. 高空远程滑翔鱼雷弹道建模与仿真[J]. 弹箭与制导学报, 2012, 32(2): 144-146.Zhang Bo, Song Bao-wei, Wang Si-ling. Modeling and Tr- ajectory Simulation for High Altitude Longrange Gliding Torpedo[J]. Journal of Projectiles, Rockets, Missiles and Guidance, 2012, 32(2): 144-146.

[10] 帅智浩, 严海, 曹小娟, 等. 高空投送载体组合结构模态分析[J]. 鱼雷技术, 2015, 23(2): 81-85.Shuai Zhi-hao, Yan Hai, Cao Xiao-juan, et al. Modal An- alysis on the Composite Structure of High Altitude Deli- very Carrier[J]. Torpedo Technology, 2015, 23(2): 81-85.

[11] 张克涵, 温杰, 顾李冯, 等. 远程高空滑翔UUV的最优控制设计与仿真[J]. 测控技术, 2013, 32(3): 66- 69.Zhang Ke-han, Wen Jie, Gu Li-feng, et al. Optimal Cont- rol Design and Simulation of High-Altitude Long-Range Glider UUV[J]. Measurement & Control Technology, 2013, 32(3): 66-69.

[12] 刘哲, 王立文, 张秦南. 火箭助飞鱼雷纵向通道制导系统参数设计及仿真[J]. 鱼雷技术, 2006, 14(3): 52-54.Liu Zhe, Wang Li-wen, Zhang Qin-nan. Controller Para- meters Design and Simulation of Vertical Channel Guidance System for Rocket-Assisted Torpedo[J]. Torpedo Technology, 2006, 14(3): 52-54.

[13] 穆育强, 盛安冬. 基于复合制导的简易航弹制导控制系统设计[J]. 火力与指挥控制, 2010, 35(5): 83-85.Mu Yu-qiang, Sheng An-dong. Design of Guidance Control System based on Combined Guidance for Simple Guided Bomb[J]. Fire Control & Command Control, 2010, 35(5): 83-85.

[14] 赵红志. P-3C型“猎户座”岸基反潜巡逻机[J]. 环球军事, 2001(10): 10-12.

Trajectory Design of High-Altitude Gliding Torpedo Based on Optimal Guidance Law

CHEN Jia-jie, WANG Zhong, CAO Xiao-juan, ZHANG Qin-nan, CAI Wei-jun,

(The 705 Research Institute, China Shipbuilding Industry Corporation, Xi’an 710077, China)

In the process of attacking submarines, the high-altitude gliding torpedo can increase the attack range by gliding extended range, and can attack outside the submarine defense area to effectively improve the survivability of carrier aircrafts. The air trajectory of the high-altitude gliding torpedo includes gliding extended range trajectory and parachute trajectory, and at the end of the gliding extended range trajectory, the torpedo will separate from its glider and open the parachute. As a result, the terminal trajectory constraint of the high-altitude gliding torpedo is more complicated than normal airdropped torpedo. To satisfy the terminal position and terminal trajectory inclination angle constraints, a trajectory model of high-altitude gliding torpedo is established based on the optimal control principle, and an optimal guidance law is proposed in this paper. According to the optimal guidance law and the overload control principle, the integral overload control method of the glider is given. The trajectory simulations between the traditional proportional navigation(PN) and the proposed optimal guidance law are compared. The results show that PN can satisfy the position constraint, which contains the horizontal control accuracy and the separation altitude of glider and torpedo, but exerts no control over the trajectory inclination, while the optimal guidance law can satisfy not only the constraints of horizontal control accuracy and separation altitude, but also the constraint of terminal trajectory inclination angle.

high-altitude gliding torpedo; trajectory optimal control; proportional navigation(PN); optimal guidance law

TJ630.33; TJ765.22

A

2096-3920(2020)03-0278-06

10.11993/j.issn.2096-3920.2020.03.006

2019-07-22;

2019-09-05.

陈嘉杰(1995-), 男, 在读硕士, 主要研究方向为鱼雷总体技术.

陈嘉杰, 王中, 曹小娟, 等. 基于最优导引律的高空滑翔鱼雷弹道设计[J]. 水下无人系统学报, 2020, 28(3): 278- 283.

(责任编辑: 杨力军)