基于小波变换的电子音乐信号降噪算法
2020-06-30周玉花刘勇飞
周玉花 刘勇飞
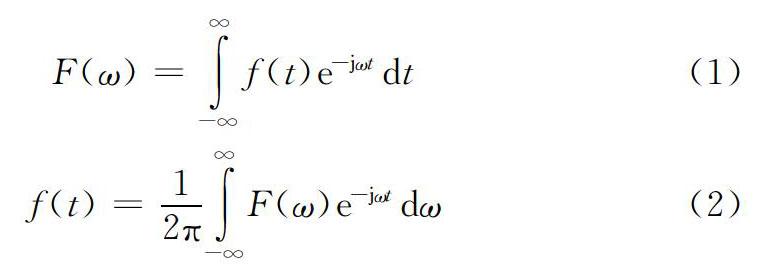

摘 要: 电子音乐信号受到多种因素的影响,包含了大量的噪声,直接影响电子音乐信号的后续处理。为了提高电子音乐信号质量,改善信号的信噪比,针对当前电子音乐信号降噪算法存在的局限性,设计了一种基于小波变换的电子音乐信号降噪算法。首先分析电子音乐信号降噪的研究现状,指出各种电子音乐信号降噪算法的弊端,然后采集电子音乐信号;对其进行截尾操作,提取最有效的电子音乐信号,最后引入小波变换对电子音乐信号进行多尺度分解和重构操作,过滤掉电子音乐信号中的噪声。并采用Matlab 2018编程实现电子音乐信号降噪仿真实验。结果表明,小波变换克服了当前电子音乐信号降噪算法的不足,电子音乐信号降噪的精度高,能够有效识别噪声,使得降噪后的电子音乐信号具有更高的信噪比。
关键词: 电子音乐; 信号质量; 仿真实验; 噪声过滤; 信号信噪比
中图分类号: TP 391 文献标志码: A
Denoising Algorithm of Electronic Music Signal Based on Wavelet Transform
ZHOU Yuhua1, LIU Yongfei2
(1. Ministry of Basic and Quality Education, Qinghai College of Architectural Technology, Qinghai Xining 810012, China;
2. The Computer College, Qinghai Normal University, Xining, Qinghai 810012, China)
Abstract:
Electronic music signal is affected by many factors, including lots noises, which directly affects the follow-up processing of electronic music signal. In order to improve the quality of electronic music signal and reduce the signal-to-noise ratio, aiming at the limitations of current electronic music signal denoising algorithm, a denoising algorithm based on wavelet transform is designed. Firstly, the electronic music signal is analyzed. The research status of music signal noise reduction is summarized, the disadvantages of various electronic music signal noise reduction algorithms are pointed out, then electronic music signals are collected and their tails are truncated, the most effective electronic music signals are then extracted, finally wavelet transform is introduced to carry out multi-scale decomposition and reconstruction of electronic music signals, and filter out the noise in electronic music signals. Matlab 2018 is used to complete electronic music signal noise reduction simulation experiments. The results show that the wavelet transform overcomes the shortcomings of the current electronic music signal denoising algorithms. The electronic music signal denoising accuracy is high. It can identify noise, the electronic music signal after denoising has a higher signal-to-noise ratio.
Key words:
electronic music; signal quality; simulation experiment; noise filtering; signal to noise ratio
0 引言
隨着信息技术和多媒体技术不断发展,两者不断的融合,很多音乐创作人通过计算机进行音乐合成,产生了大量的电子音乐。在电子音乐合成和传输过程中,由于外界环境和其它因素的综合作用,电子音乐信号中可能包含有一些噪声,这些噪声会对电子音乐信号进行污染,导致电子音乐信号质量下降,严重时,得到电子音乐信号无法描述实际音乐表示的内容,因此需要对电子音乐信号进行降噪处理研究,还原真实的电子音乐信号具有十分重要的实际意义[1-3]。
近几年来,国内外的一些电子音乐合成研究机构对电子音乐降噪高度重视,当前电子音乐信号降噪技术划分为两大类:一类是基于硬件技术的电子音乐信号降噪方法,另一类是基于软件技术的电子音乐信号降噪方法[4]。硬件技术的电子音乐信号降噪效果很好,但是由于其要求一定的辅助设备,不仅增加了电子音乐信号降噪的成本,而且对操作人员的专业程度相当高,因此通用性比较差[5];相对于硬件技术,软件技术的电子音乐信号降噪成本更加便宜,可以对各种类型的噪声进行过滤操作,成为当前电子音乐信号降噪的主要研究方向[6-8]。软件技术的电子音乐信号降噪方法又可划分为两种类型:基于空间域和基于变换域的电子音乐信号降噪算法,空间域的电子音乐信号降噪算法可以直接对噪声进行处理,十分容易去除一些重要、有用的信号,导致去噪后的电子音乐信号不完整,实际应用范围比较窄;变换域算法主要有傅里叶变换的电子音乐信号降噪算法,其对电子音乐信号进行适当变换,然后在变换的空间进行去噪,但是存在去噪精度低等弊端[9-10]。
为了提高电子音乐信号质量,改善信号的信噪比,针对当前电子音乐信号降噪算法存在的局限性,设计了一种基于小波变换的电子音乐信号降噪算法,采用Matlab 2018编程实现电子音乐信号降噪仿真实验。结果表明,小波变换的电子音乐信号降噪精度高,获得了理想的电子音乐信号。
1 传统的电子音乐信号降噪算法以及不足
基于热传导方程,Fourier提出了傅里叶变换算法,其是一种很好的信号分析工具,其具有正变换和逆变换两种形式,如式(1)、式(2)所示。
傅里叶变换将原始电子音乐信号看作是一些不同大小频率、振幅的电子音乐信号累加形成,通过振幅较大的分量来分析相对应的频率信号,由于噪声信号具有一定的周期性变化特点,因此可以过滤掉电子音乐信号中的噪声。对于变化比较平稳和确定的电子音乐信号,傅里叶变换可以对变化特点进行精确的刻画,但是对于非平衡和随机变化的电子音乐信号,傅里叶变换缺陷就体现出来,其只能从整体上分析电子音乐信号,无法从局部上描述电子音乐信号的特性,这样噪声比较复杂的电子音乐信号,噪声无法有效去除,为此有学者提出了短时傅立叶变换。短时傅立叶变换通过加窗操作可以对电子音乐信号实现局部化处理。
时变电子音乐信号x(t)与有限时窗信号ω(t)进行乘积运算,称之为傅立叶变换,在一定窗口内,时变电子音乐信号是平衡的,如式(3)所示。
短时傅立叶变换一定程度中克服了传统傅立叶变换存在的不足,但是当电子音乐信号随机变化比较剧烈时,其适应能力差,噪声经常出现欠去除现象,降低了电子音乐信号的质量。
2 小波变换的电子音乐信号降噪算法
2.1 小波变换
2.2 小波变换的电子音乐信号降噪步骤
Step1:采集电子音乐信号,对其进行截尾操作,提取最有效的电子音乐信号。
Step2:对原始电子音乐信号进行一定的处理,使其能够满足小波变换处理的要求。
Step3:采用小波变换对电子音乐信号进行多尺度分解,得到一系列不同频率的电子音乐信号分量,从而得到相对应的小波系数。
Step4:分析有用的电子音乐信号和噪声在频率系数尺度的分布特征,本文采用阈值方法对高频小波系数置零,由于噪声与高频小波系数相对应,低频小波系数保留。
Step5:将保留后的小波频率系数进行重构,得以受噪声污染的电子音乐信号。
综合上述可知,小波变换的电子音乐信号降噪原理,如图1所示。
电子音乐信号降噪过程中的小波阈值函数选取十分关键,当前有两种小波阈值函数:硬阈值和软阈值,它们分别定义如式(10)、式(11)所示。
式中,ω表示电子音乐信号分解后的小波系数,ωλ表示进行阈值处理后的电子音乐信号的小波系数,λ表示去噪的阈值,其取值方式如式(12)所示。
式中,σn与L分别为噪声标准差和小波系数总数。
3 电子音乐信号降噪算法的性能测试
3.1 实验对象
为了分析小波变换的电子音乐信号降噪性能,采用Matlab 2018编写电子音乐信号降噪程序,并采用一段电子音乐信号作为测试实验对象,其变化曲线如图2(a)所示。加入一定的噪声后,电子音乐信号变化曲线如图2(b)所示。
3.2 降噪效果的主观分析
选择傅里叶变换的电子音乐信号降噪算法和文献[10]的电子音乐信号降噪算法在相同的实际环境下,对于图2的含噪电子音乐信号进行降噪仿真实验,得到的结果如图3所示。
对图3的电子音乐信号降噪效果进行对比和分析可以发现,对比算法的电子音乐信号降噪效果差,噪声去除不干净,去噪后的电子音乐信号失真效果比较严重,一些有用的信号被误作噪声去除掉了,而小波变换的电子音乐信号降噪后,与原始信号的变化曲线拟合精度相当高,能够有效过滤掉电子音乐信号中的噪声,获得了理想的降噪效果,體现了小波变换在降噪过程中的优势。
3.3 降噪效果的客观分析
为了对电子音乐信号降噪效果进行更加精确分析,采用信噪比对降噪后的电子音乐信号进行评价,信噪比的计算式如式(13)—(15)所示。
式中,f(n)和N(n)分别表示有用的电子音乐信号和噪声。
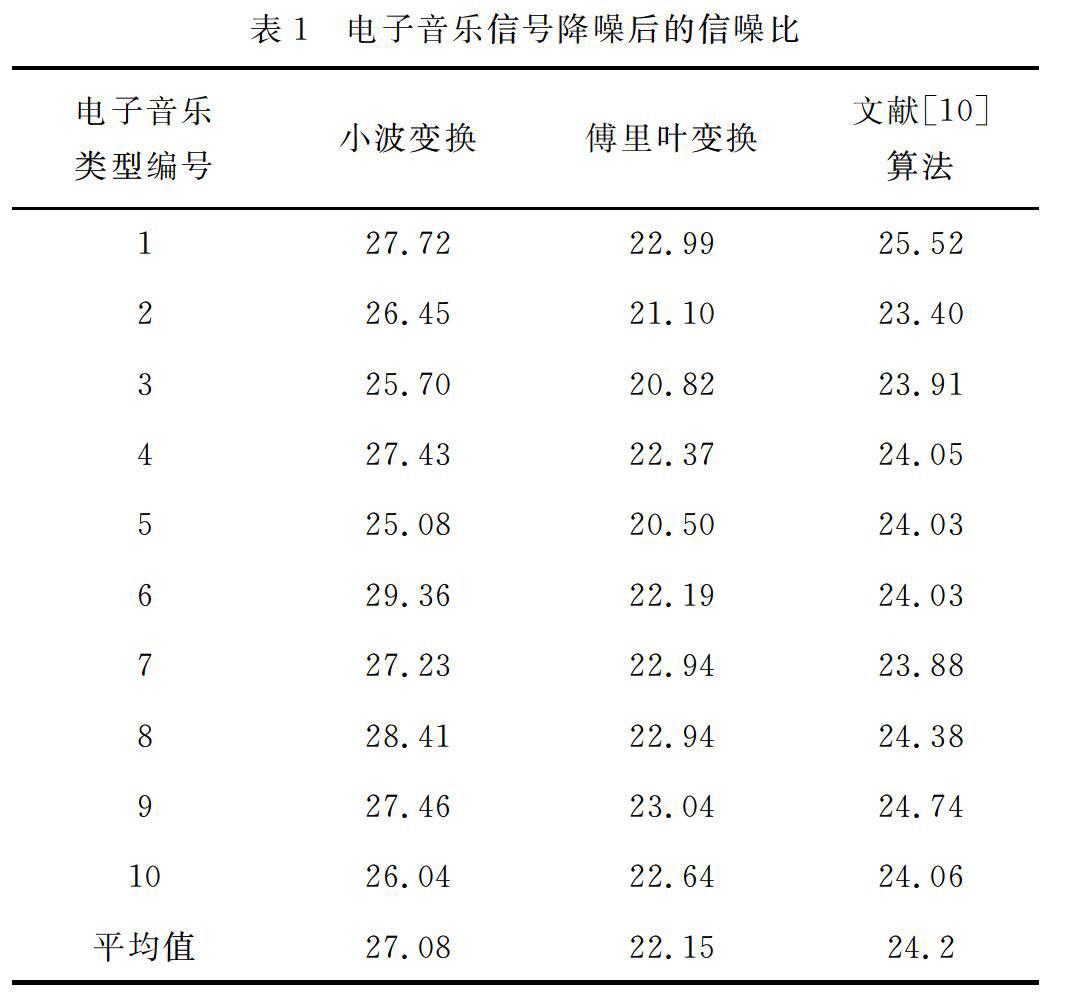
选取10种类型的电子音乐信号作为研究对象,分别给它们加入不同程度的噪声,采用三种算法分别对10种含有噪声的电子音乐信号进行降噪处理,统计它们降噪后的电子音乐信号信噪比,结果如表1所示。
对表1的电子音乐信号信噪比进行分析可以知道,小波变换的电子音乐信号降噪后信噪比要远远高于傅里叶变换和文献[10]的降噪算法,改善了电子音乐信号质量。
4 总结
针对传统电子音乐信号降噪算法存在的降噪精度低,噪声残留大的缺陷,为了获得干净的电子音乐信号,设计了小波变换的电子音乐信号降噪算法,仿真测试结果表明,对于不同类型的噪声,小波变换均可以有效识别,对它们进行高精度的去除,不仅电子音乐信号信噪比高,而且降噪效果要明显优于当前其它电子音乐信号降噪算法,具有十分广泛的应用前景。
参考文献
[1] 刘天华. 基于多特征融合和神经网络的电子音乐分类模型[J].现代电子技术, 2018, 41(19): 173-176.
[2] 周婧,范凌云. 基于最小二乘支持向量机的电子音乐识别研究[J].现代电子技术, 2018, 41(9): 109-112.
[3] 廖逢钗,李鹏,徐波. 音乐噪声环境下的双声道语音活动检测[J].信号处理, 2009, 25(11): 1820-1824.
[4] 邓高峰,叶金才,王国富, 等. 基于蜂群算法和新阈值函数的信号降噪算法[J]. 计算机应用研究, 2019,36(10):2974-2976.
[5] 孔薇,杨杰,周越. 基于独立成分分析的强背景噪声降噪方法[J].上海交通大学学报, 2004(12): 1957-1961.
[6] 刘迪,关欣,李锵,等. 基于鲁棒主成分分析的音乐信号降噪[J].计算机工程, 2016, 42(9): 292-296.
[7] 杨璐,李醒飞,纪越,等. 基于EMD-DFA-NLM的电涡流传感器信号降噪方法[J].传感技术学报, 2019, 32(9):1318-1323.
[8] 李占辉,刘晓强,李柏岩. 小波域降噪方法及其在历史音频保护中的应用[J].噪声与振动控制, 2010, 30(4):68-71.
[9] 朱文斌,雷秉山,雷志勇.基于小波变换的红外探测系统信号降噪[J].红外技术, 2018, 40(11): 1047-1051.
[10] 陈光武,刘孝博,王迪,等. 基于改进小波变换的MEMS陀螺信号降噪算法[J].电子与信息学报, 2019,41(5):1025-1031.
(收稿日期: 2019.07.23)
