基于灰靶决策模型的燃气管道腐蚀风险对比
2020-06-30张雪娇马旭卿郭保玲张玉星
张雪娇, 马旭卿, 郭保玲, 张玉星
(北京市燃气集团研究院, 北京 100011)
1 概述
随着城市燃气的快速发展,燃气管网敷设的数量和压力等级越来越多,埋地管道所处的环境也越来越复杂[1-2]。受周围环境的影响,埋地钢质燃气管道容易发生腐蚀,并且腐蚀风险与所处的环境关系密切,比如管道敷设在不同的土壤中时,其腐蚀风险不同,在不同的压力等级下,管道的腐蚀风险也有差异。管道腐蚀后会发生一系列危险情况,影响燃气管网的正常运行,威胁人民群众的生命财产安全,造成不可忽视的经济损失[3-5]。埋地钢质燃气管道的腐蚀是管道周围环境以及管道自身条件多参数长期共同作用的结果。为对比多参数影响下的埋地钢质燃气管道的腐蚀风险,本文结合某城市不同环境下的埋地钢质燃气管道腐蚀参数的现场实际数据,选取土壤电阻率[6]、管道周围环境pH值、管地电位[7]、硫酸盐还原菌(SRB)含量[8]、管道运行压力、管道埋深以及服役时间7个影响管道腐蚀风险的重要参数,建立埋地钢质管道腐蚀风险多参数灰靶决策模型[9-14],利用熵值法求取参数权重[15],计算待评价管道的综合靶心距,通过综合靶心距比较不同管道的腐蚀风险,从而为比较不同管道在多参数影响下的腐蚀风险提供了一种可行可靠的方法。
2 燃气管道腐蚀影响参数表征
本文以某城市不同环境下的5段埋地钢质燃气管道为研究对象,进行5段管道腐蚀风险的比较。在现场实际调研中发现,土壤电阻率、管道周围环境pH值、管地电位、硫酸盐还原菌含量、管道运行压力、管道埋深以及管道服役时间是影响埋地钢质燃气管道腐蚀的重要参数。本文基于某城市不同环境下的埋地钢质燃气管道的现场实际数据,列出以上7个影响管道腐蚀的风险参数在5段管道中的值,见表1。
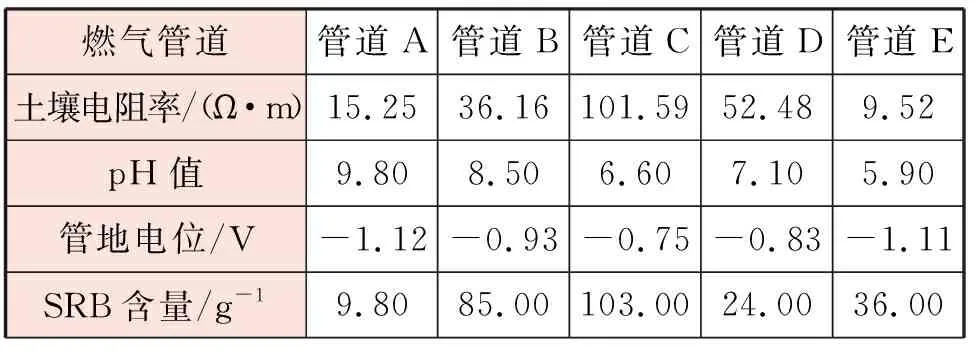
表1 燃气管道腐蚀影响参数现场实际数据
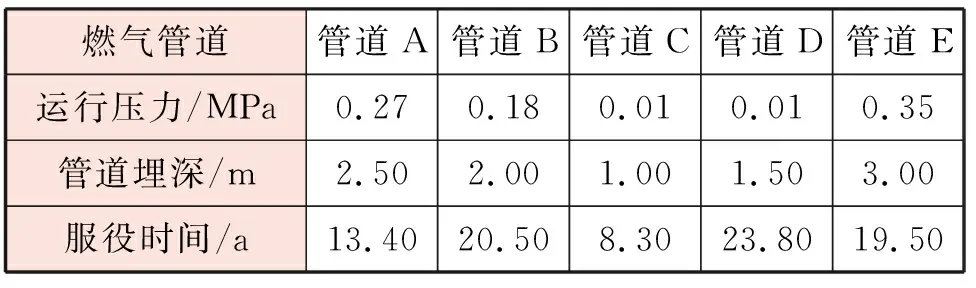
续表1
3 多参数灰靶决策模型描述
多参数灰靶决策模型是灰色系统理论中解决多参数决策问题的重要方法,本文利用该方法来比较不同管道在多参数影响下的腐蚀风险。其主要思想是对参数集进行初始化处理得到无量纲参数,即灰靶,所有研究决策对象都分布在灰靶上。由于各参数对决策对象的作用不同,采用熵值法确定参数权重。在灰靶上选取靶心作为决策标准,比较决策点与靶心点的距离,通过计算决策点的靶心距进行决策对象间的风险排序,从而得到不同管道在多参数影响下的腐蚀风险对比结果。
3.1 效果样本决策矩阵描述
本文5段管道的腐蚀风险是待评价决策对象,它们组成决策集J,J={J1,J2,J3,J4,J5};7个评价参数组成参数集C,C={C1,C2,…,C7};决策集J对参数集C组成了效果样本值aij(i=1,2,…,5;j=1,2,…,7),从而得到矩阵A,矩阵A从第1行到第5行分别代表管道A、管道B、管道C、管道D、管道E,从第1列到第7列分别代表土壤电阻率、管道周围环境pH值、管地电位、SRB含量、运行压力、管道埋深、服役时间的具体值。矩阵A如下:

式中A——燃气管道腐蚀风险的效果样本决策矩阵
aij——燃气管道腐蚀风险参数的效果样本值
3.2 参数集初始化处理与正负靶心确定
本文选取的7个参数具有不同的量纲和量级,为了消除效果样本决策矩阵值在量纲和量级上的差异,增强不同腐蚀参数之间的可比性,需要对原始效果样本决策矩阵进行初始化处理。初始化处理的方法较多,比如灰色极差变换、区间值化变换、百分比变换等。针对这些方法中存在“只奖不罚”的不足,本文总结前人经验,引入“奖优罚劣”算子进行初始化处理。其基本原则为:决策对象的参数值优于均值,赋以[0,1]内的正值;决策对象的参数值劣于均值,赋以[-1,0]内的负值。
令:
(1)

n——待评价燃气管道数量,本文n=5
j——燃气管道腐蚀影响第j个参数
7个参数中,土壤电阻率、管道周围环境pH值、管道运行压力、管道埋深为低风险腐蚀参数,参数值越大,管道腐蚀风险越低;管地电位、SRB含量和服役时间为高风险腐蚀参数,参数值越大,管道腐蚀风险越高。
设经过初始化处理后,效果样本值aij变换为无量纲样本值bij(i=1,2,…,5;j=1,2,…,7)。
对低风险腐蚀参数,有:
(2)
对高风险腐蚀参数,有:
(3)
式中bij——燃气管道腐蚀风险参数的无量纲样本值
max{aj}——第j项参数的最大值
min{aj}——第j项参数的最小值
利用式(1)、(2)、(3)对以上参数进行初始化变换,得到矩阵B,矩阵B从第1行到第5行分别代表管道A、管道B、管道C、管道D、管道E,从第1列到第7列分别代表土壤电阻率、管道周围环境pH值、管地电位、SRB含量、运行压力、管道埋深以及服役时间的无量纲值。矩阵B如下:
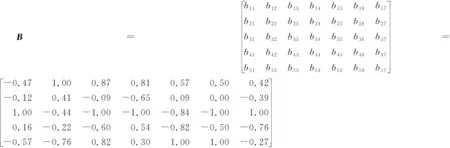
式中B——燃气管道腐蚀风险的无量纲决策矩阵
由无量纲决策矩阵B可以看出,经过初始化处理,B中所有参数值都在[-1,1]之内,与“奖优罚劣”的基本原则相吻合。
对任意bij,有:
bi=(bi1,bi2,bi3,bi4,bi5,bi6,bi7)
式中bi——决策方案i的效果向量
设最优效果向量为灰靶决策模型的正靶心b+,它是由初始化参数值最优值构成,为:
其中:
则正靶心为:
b+={1.00,1.00,0.87,0.81,1.00,
1.00,1.00}
设最劣效果向量为灰靶决策模型的负靶心,它是由初始化参数值最劣值构成,为:
其中:
则负靶心为:
b-={-0.57,-0.76,-1.00,-1.00,
-0.84,-1.00,-0.76}
4 基于熵值法的参数权重计算
权重的计算方法有很多,例如网络分析法和层次分析法,为了使权重的计算不带有主观色彩,本文采用熵值法计算参数的权重。利用待评价管道腐蚀风险参数的固有值,通过计算得到各个参数的信息熵,信息熵越小,信息无序度越低,信息效用值越大,参数权重越大。熵值法的优点是直接利用效果样本决策矩阵进行权重的计算,不会引入决策者的主观判断,计算的权重更加准确客观。
熵值法的具体计算步骤如下:
① 效果样本决策矩阵参数标准化处理
正向指标是指参数值越大,腐蚀风险越低的指标,本文中土壤电阻率、管道周围环境pH值、管道运行压力、管道埋深属于正向指标。对于正向指标有:
(4)
负向指标是指参数值越大,腐蚀风险越高的指标,本文中管地电位、SRB含量和管道服役时间属于负向指标。对于负向指标有:
(5)
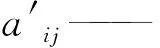
② 计算管道i第j项参数值的比重
设管道i第j项参数的比重为Yij,则有:
(6)
式中Yij——管道i第j项参数的比重
③ 计算参数的信息熵
(7)
式中ej——第j项参数的信息熵
④ 计算参数的信息熵冗余度
dj=1-ej
(8)
式中dj——第j项参数的信息熵冗余度
⑤ 计算参数的权重
(9)
式中Wj——第j项参数的权重
m——参数个数,本文m=7
由(4)~(9)式,得:
7项参数的信息熵为:
e=(0.67,0.91,0.50,0.73,0.67,0.80,
0.82)
最后得到熵值法计算的参数权重为:
W=(0.17,0.05,0.26,0.14,0.17,
0.11,0.09)
5 管道腐蚀风险对比
① 燃气管道腐蚀综合靶心距计算
管道i的实际参数值与正负靶心值的接近程度反映了管道腐蚀风险的高低。决策方案i的效果向量bi的综合靶心距越小,对应的管道腐蚀风险越低。
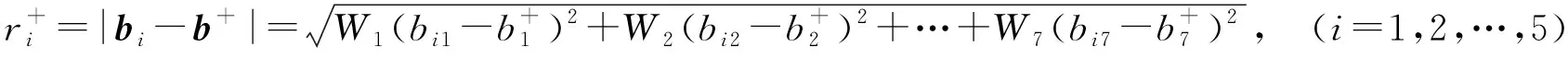
(10)
(11)


由式(10)、(11)计算出各管道正、负靶心距,结果见表2。

表2 埋地燃气管道正、负靶心距
正靶心与负靶心之间的距离称为正负靶心距,记为rb,其计算公式为:
rb=|b+-b-|=
(12)
式中rb——正负靶心距
由式(12)得出正靶心与负靶心之间的距离为1.81。

(13)

θ——效果向量bi在正、负靶心连线上的投影角度
由式(13)计算出各燃气管道综合靶心距,结果见表3。

表3 埋地燃气管道综合靶心距
由表3得到综合靶心距排序:
② 埋地钢质燃气管道腐蚀风险比较与分析
由综合靶心距的排序结果得到埋地燃气管道腐蚀风险对比,风险由高到低为:管道C、管道D、管道B、管道E、管道A。管道C为该市某路段小区内一段低压管道,经现场初步测试,管地电位比正常管地电位偏高,有部分杂散电流从管道流出造成管道腐蚀,并且管道没有施加阴极保护,腐蚀风险较大。
6 结论
① 以埋地钢质燃气管道为研究对象组成方案集,选取土壤电阻率、管道周围环境pH值、管地电位、硫酸盐还原菌含量、管道运行压力、管道埋深、服役时间为影响管道腐蚀的参数组成参数集,建立灰靶模型效果样本决策矩阵,利用“奖优罚劣”算子对其进行初始化处理,得到决策矩阵。
② 采用熵值法计算管道腐蚀参数权重,不涉及决策者的主观判断,计算结果准确客观。
③ 由决策矩阵得到灰靶模型的正负靶心,计算各个管道参数集的综合靶心距,利用综合靶心距对不同管道的腐蚀风险进行比较,对比结果与现场测试结果相吻合,表明基于熵值法确定权重的多参数灰靶决策模型可以应用于多参数影响下的管道腐蚀风险对比。
