基于改进Dijkstra 算法的自驾游最优路径规划研究

刘洋洋

（郑州师范学院地理与旅游学院，河南 郑州450044）

随着经济的高速发展和私家车的大量普及，相比传统的旅行社组织的团体旅游，如今的游客们越来越倾向于灵活随性的自驾游。与传统的集体参团旅游不同，自驾游是一种新的旅游形态，在选择景点、参与过程和个人体验等方面，自驾游能为游客提供更加随性自如的旅游空间，与以往的旅游方式相比，自驾游所体现的自由化与个性化、灵活性与舒适性、选择性与季节性等内在特点，具有更加独特的魅力和吸引力。据调查显示，游客一般喜欢在节假日外出旅游，但由于假期时间有限，再加上交通条件、天气条件、驾驶路线等各种因素的影响和制约，因此对游客来说，旅游景点的选择和出行路线的规划就显得尤为重要。自驾游时，首先需要制定一条科学合理的旅游路线，但由于目前常用的地图导航软件一般只提供从游客位置到单个旅游目的地两点之间的最优路径，并不能对多个旅游景点间的最优路径进行规化。鉴于此点，为满足游客自驾游时的具体需求，本文改进了用于求两点间最短路径的Dijkstra 算法，以帮助游客实现多景点间的最优旅游路线[1-5]。

1 Dijkstra 算法

Dijkstra（迪杰斯特拉）算法是解决最短路径问题的经典算法，常用于在非负权值图中计算一个节点到其他所有节点的最短路径[7-8]。该算法的计算流程如下所示：

1.1 首先初始化存放已确定的最短路径节点集合Y 和未确定的最短路径节点集合Q，然后通过权图的邻接矩阵来初始化起始点到其他所有节点的最短路径长度N。如果起始点到其他节点有连接弧，则对应的值为连接弧的权值，如果没有，则默认对应的值为极大值。

1.2 其次选择N 中的最小值N[i],记N[i]为起始点v 到点i的最短路径长度，把点i 从集合Q 中取出来放入集合Y 中。

1.3 然后根据节点i 来更新修改数组N 中起始点v 到集合Q 中的节点M所对应的路径长度值。

图1 采用贪婪思想的Dijkstra 算法

1.4 最后重复上述步骤1.2 和步骤1.3 的操作，直到找出起始点到所有节点的最短路径为止。

Dijkstra 算法的核心思想是以遍历的形式找到图中所有节点的最短路径，从而确立目标点的最短路径。在使用Dijkstra 算法计算最优路径时，为了提高算法效率，一般会在寻找路径的穷举过程中加入贪婪思想[9-10]。大致过程如下所示：

1.4.1 设C 为约束节点的集合，P 为找到的路径，G 为图，x为任一约束点，s 为路径起点，t 为终点。

1.4.2 首先计算s 到C 中每个约束点的距离，并按距离对C中的约束点进行排序，优先选择离s 近的约束点，最后选择离S远的约束点。

1.4.3 在计算s 到C 中每个约束点的距离时，会生成以s 为根的最短路树，从这棵树中，可直接取到Dijkstra（s，x，G）的结果。如果想取到Dijkstra（s，x，G-C+x）的结果，可修改生成最短路树的过程，使其遇到约束点时不再生长，即约束点必须是最短路树的叶节点[10]。加入贪婪思想的Dijkstra 算法虽能提高算法效率，但在很多情况下计算效果并不理想，如图1 所示，在计算s到t 的路径过程中，加入贪婪思想的Dijkstra 算法会按照黑线顺序来穷举约束节点，这样很容易计算失败。相反，如果按红线顺序穷举约束节点，成功率就会提高很多。

图2 改进后的Dijkstra 算法

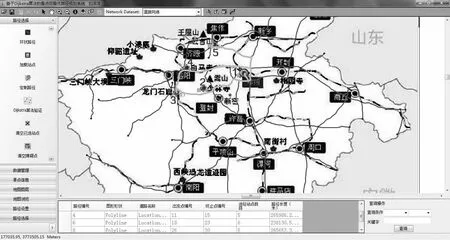
图3 河南自驾游最优路线

2 算法改进

针对上述问题，该文对Dijkstra 算法进行了改进，使其在计算每个约束点到s、t 的距离时，优先选择离s 近且离t 远的点，然后再选择离s 远且离t 近的点。最后针对每个约束点，计算一个权重，该权重是以约束点为自变量的函数，称为指导函数h。得出权重结果后，对权重进行排序，权重小的优先处理。

h（c）= |sc| - |ct| + |xc| （|sc|表示s 到c 的最短距离）(1)

采用改进后的算法，只需经过几轮迭代，便可精确计算出s到x 的最优路径，然后再依次得出x 到剩余约束点的距离，如图2 所示。在运用该算法进行计算时，各约束点到s、t 的距离只需要计算一次，不用在每次迭代中都重复计算，有效的提高了计算成功率和计算效率。

实现该算法的伪代码如下所示：FindPath（s，t，G，C）： return P

BEGIN

对C 中的每个约束点，计算其引导函数h(c)，按h(c)对C 进行排序

3 实验验证

对Dijksatra 算法进行优化后，本文以C#语言为编程语言，以.net 为开发环境，以SQL Server 为数据库，对ArcGIS 进行了二次开发，成功搭建了基于景点间最优路径规划的Dijkstra 算法验证系统。

鉴于河南省丰富的旅游资源，本文选取了该省若干知名景点作为实验对象，规划了一条自驾游河南的最优路线。首先，本文设定省会郑州为出发点和终点，然后选取少林寺、龙门石窟、白马寺、云台山四大景点为旅游目的地，最后规定约束条件为：游客从郑州出发，以最优路径游览以上四个景点后返回郑州。条件设定完毕后，在Dijkstra 算法验证系统的主界面地图中标出以上四个景点的准确位置，然后点击Dijkstra 算法验证按钮，通过改进后的Dijkstra 算法计算，系统成功得出了自驾游河南的最优路径。如图3 所示，从图中序号顺序及高亮显示的路径可以看出，自驾游河南的最优路线为：郑州→白马寺→龙门石窟→少林寺→云台山→郑州。经实验结果表明，改进后的Dijkstra 算法准确高效的计算出了多约束条件下多个景点间的最优旅游路径。

4 结论

随着私家车的大量普及，自驾游已逐渐成为人们外出旅游的首选方式。基于游客自驾游时对景点间最优路径的需求，该文对Dijkstra 算法进行了改进，加入了指导函数h，使其能够有效实现多景点间最优路径的计算。最后，实验结果表明，改进后的Dijkstra 算法成功规实现了以郑州为起点和终点，以少林寺、龙门石窟、云台山和白马寺为旅游景点的多景点间的自驾游最优路径，从而验证了该算法的合理性和实用性。