双馈风力发电机无速度传感器控制方法研究

海樱 宁丙辰

摘要：建立了可用于控制算法研究的双馈风力发电机数学模型，在确定电网电压定向矢量控制策略的基礎上，提出了采用基于转子电流的模型参考自适应方法进行电机转速观测的无速度传感器控制方法。在双馈风力发电系统模拟实验平台上对控制方法进行了实验验证，结果证明了无速度传感器定向矢量控制策略的有效性。

关键词：双馈风力发电机;无速度传感器;模型参考自适应

0    引言

风能作为一种可再生清洁能源，在世界范围内得到了广泛的应用。双馈风力发电系统采用转子双馈发电机，其功率变换是在转子侧实现的，转子侧电路流过的功率由转差功率决定，一般仅为发电机定子额定功率的30%左右[1]，大大降低了变换器的容量和成本。因此，该方案在兆瓦级以上风电系统中应用尤为广泛，发展前景十分广阔[2-3]。

在双馈风电控制系统中，需要实时采集电机转子的转速或位置信号，通常是通过安装光电编码器等速度传感器或位置传感器来实现的。然而传感器的安装一定程度上降低了系统的可靠性[4]，增加了系统的运行和维护成本。近40年来，国内外学者对无速度传感器控制策略展开了研究，一般采用直接计算、状态估计、参数辨识、间接测量等方法对转子的速度进行计算[5-6]。

本文对双馈风力发电机的控制算法展开了研究，在确定了电网电压定向矢量控制策略的基础上，采用以转子电流为观测量的模型参考自适应方法进行电机转速辨识，实现了系统的无速度传感器定向矢量控制。最后在实验室搭建的双馈风电模拟实验平台上进行了算法验证，证明了控制策略的有效性。

1    双馈发电机的数学模型

为了研究双馈风力发电机的控制方法，首先要建立可用于控制算法研究的数学模型。基于双馈电机在三相静止坐标系下具有非线性、高阶、强耦合的特点[7]，为便于分析研究，通常采用坐标变换的方法[8]，将其在三相静止坐标系下的数学模型变换到（d，q）同步旋转坐标系下。同步旋转坐标系下的电压方程式为：

2    电网电压定向矢量控制策略

本文采用电网电压定向矢量控制，即将同步旋转坐标系的d轴定向于电网电压空间矢量方向，由于电网电压可以直接测量，因此该定向方式不易受电机参数的影响，可以实现准确定向，保证控制算法的有效性[9]。此时，电网电压的d、q轴分量为：

双馈发电机采用转子电流环、定子侧功率环的双闭环控制策略，控制器可根据风机实际转速和电网容量需求，实时动态调节发电机输出的有功功率和无功功率。

3    无速度传感器控制策略

在双馈风电系统中，为了保证运行效率，发电机通常运行在同步转速附近，这会导致转子侧的频率和电压值都比较小，直接将电机转子反电动势或磁链作为观测量将变得非常困难[10]。考虑到电机转子电流可以直接进行测量的优势，本文将转子电流作为直接观测对象，采用基于转子电流的模型参考自适应方法，将转子电流作为模型的输出量，通过比较参考模型和可调模型的误差，并输入到自适应比较器中，不断缩小参考模型输出电流和可调模型输出电流之间的偏差，当偏差为0时，即得到转子转速。

在不考虑电机定子、转子电阻影响的情况下，由双馈电机的电压、磁链方程式，可计算出转子电流为：

在两相同步旋转坐标系下，定子电压和电流的大小与转子位置无关，因此式（8）所表示的转子电流也与转子位置角无关，可认为是准确值，将其作为参考模型。

图1所示为转子电流准确值Ir与观测值Ir′之间的矢量关系，其中，Δθ为转子电流准确值与观测值之间的角度差。

当转子电流准确值与观测值之间的角度差为0时，广义误差e即为0，此时转速值ωr稳定不变。对式（12）中的转速信号进行积分可得到转子实际位置角，该位置角是电机转子侧电压和电流进行坐标变换的必要值。将双馈风力发电机的速度辨识方法与上节提出的电网电压定向矢量控制策略结合，则得到双馈风力发电机无速度传感器控制系统。

4    实验研究

在实验室搭建的15 kW双馈风力发电系统模拟平台上对控制策略进行验证。实验平台基本结构如图2所示，主要由双馈发电机、风机模拟系统、电机侧变换器、网侧变换器及其控制系统组成。

控制系统是风电模拟平台的核心，它由两个TMS320F2812型号DSP控制器及其采集调理电路组成。DSP1负责对网侧变换器进行控制，实现网侧变换器功率因数的可调;DSP2对电机侧变换器进行实时控制，通过改变转子电流调节双馈发电机的输出功率。

在实验室模拟平台上，先后进行了系统静态实验和动态实验研究。图3为发电机转速约为800 r/min时的静态实验波形，此时风电系统为亚同步速状态。从图3中可以看出，在亚同步速运行状态下，网侧变换器电压和电流同相，变换器工作在整流状态;定子侧电压、电流保持反相，向电网输出3 kW的恒定功率。对比图3（d）和图3（e）可以看出，通过模型参考自适应辨识的电机转速与码盘读出的实际转速基本一致，其辨识精度较高。当采用无速度传感器控制方案时，系统具有优良的静态性能。

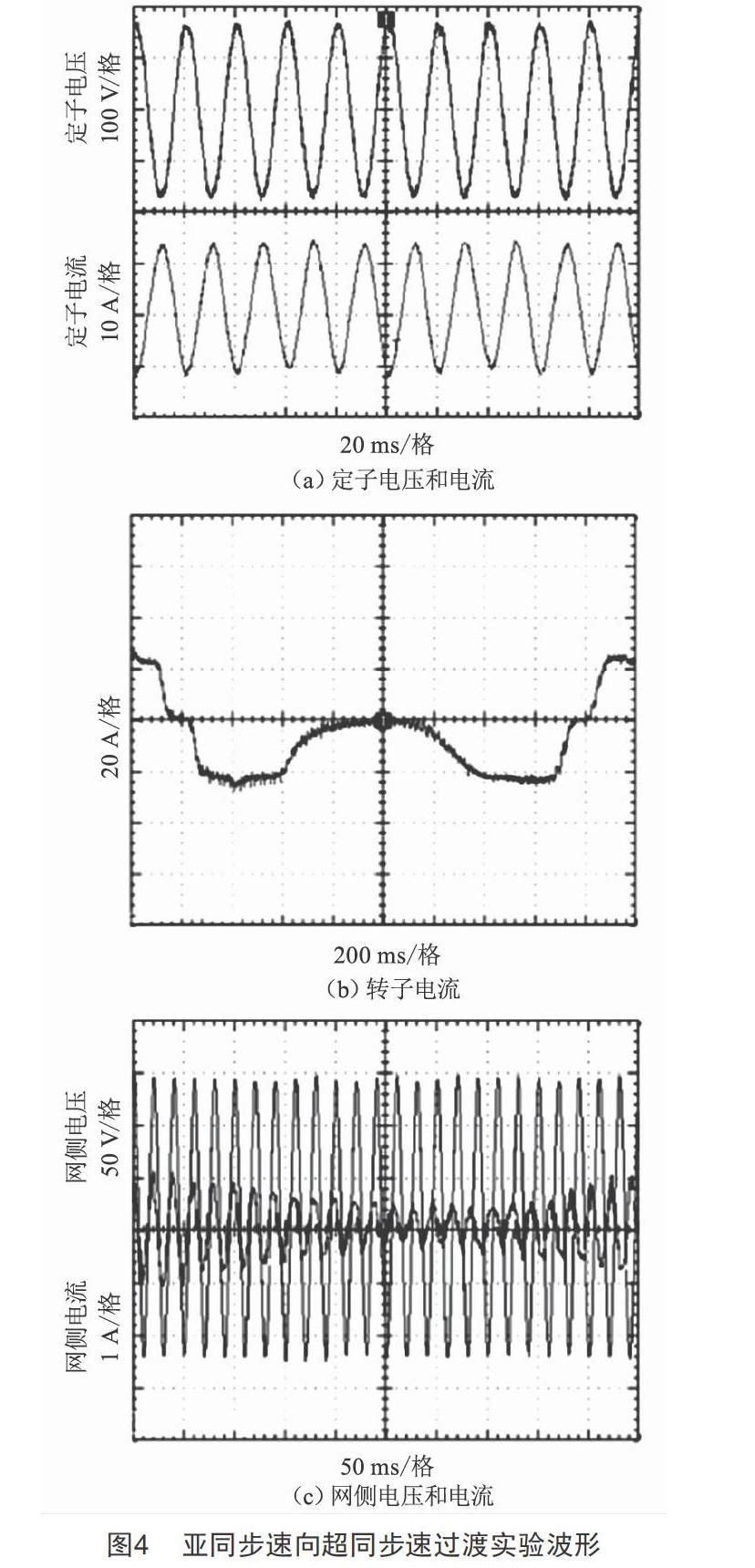
图4为动态实验过程波形，当发电机转速由800 r/min向1 100 r/min变化时，系统从亚同步速过渡到超同步速。在电机转速变化的整个过程中，定子侧的电压和电流始终反相，电机始终处于发电状态，输出功率保持不变;当电机转速变化时，转子电流的频率随之发生变化，电机转速越接近同步转速，转子电流的频率越小，当双馈电机达到同步转速1 000 r/min时，转子电流频率为0，此时，双馈电机相当于同步电机;在电机转速从亚同步速向超同步速变化的过程中，网侧变换器功率因数由1变为-1，从整流状态变化为逆变状态。在该策略的控制下，系统具有良好的动态响应。

5    结语

本文对双馈风电系统无速度传感器电网电压定向矢量控制算法进行了研究，并在实验室风电模拟平台上进行了静态和动态实验验证，结果表明该控制策略可以实现无机械速度或位置传感器下，双馈风力发电机并网运行的控制，并且具有较好的静态和动态特性。

[参考文献]

[1] 沙非，马成廉，刘闯，等.变速恒频风力发电系统及其控制技术研究[J].电网与清洁能源，2009，25（1）：44-47.

[2] 马洪飞，徐殿国，苗立杰.几种变速恒频风力发电系统控制方案的对比分析[J].电工技术杂志，2000（10）：1-4.

[3] 肖亚平，肖洒，任贝婷，等.双馈变速恒频风力发电机并网运行控制研究[J].电力学报，2017，32（5）：370-375.

[4] AMIRAT Y，BENBOUZID M E H，AL-AHMAR E.A Brief Status on Condition Monitoring and Fault Diagnosis in Wind Energy Conversion Systems[J].Renewable and Sustai-

nable Energy Reviews，2009，13（9）：2629-2636.

[5] 李永东，李明才.感应电机高性能无速度传感器控制系统——回顾、现状与展望[J].电气传动，2004，34（1）：4-10.

[6] 陈伟昌，王孝洪，田联房.基于DSP的無速度传感器异步电机矢量控制[J].电机与控制应用，2015，42（3）：20-23.

[7] 王志新，罗文广.电机控制技术[M].北京：机械工业出版社，2010.

[8] 张兴，张宗巍.PWM整流器及其控制[M].北京：机械工业出版社，2012.

[9] 海樱，崔岩梅，宁丙辰.双馈风电系统控制策略及测试研究[J].计测技术，2013，33（2）：19-23.

[10] MOHAMMED O A，LIU Z，LIU S.A Novel Sensorless Control Strategy of Doubly Fed Induction Motor and Its Examination with the Physical Modeling of Machines[J].IEEE Transactions on Magnetics，2005，41（5）：1852-1855.

收稿日期：2020-03-02

作者简介：海樱（1985—），女，河北人，工程师，研究方向：环试检测、风电变流器控制技术。