偏置曲柄连杆摇摆机构受力分析

徐智 马长帅

摘 要：對偏置曲柄连杆摇摆机构进行运动及受力分析，建立方程，进一步说明其工作原理，计算出机构运转需要的外力，为驱动机构的选型提供理论基础，同时为机构设计中材料的选用等提供理论依据。

关键词：偏置曲柄连杆摇摆机构;运动分析;受力分析

0    引言

在食品包装机械设计中，为了将盒子夹持住，需要使用到偏置曲柄连杆摇摆机构，这种机构在伺服电机的驱动下往往是成对使用，实现对包装盒的夹持。这种偏置结构由于摆动的角度比较小，可以实现短时的快速运动，完成一次对盒子的夹持动作，提高了工作效率。这种结构比较简单、易于制造，所以制造成本比较低廉。目前，随着数控加工机床的广泛使用，偏置曲柄连杆摇摆机构在制造和安装方面已不存在技术问题。

1    偏置曲柄连杆摇摆机构说明

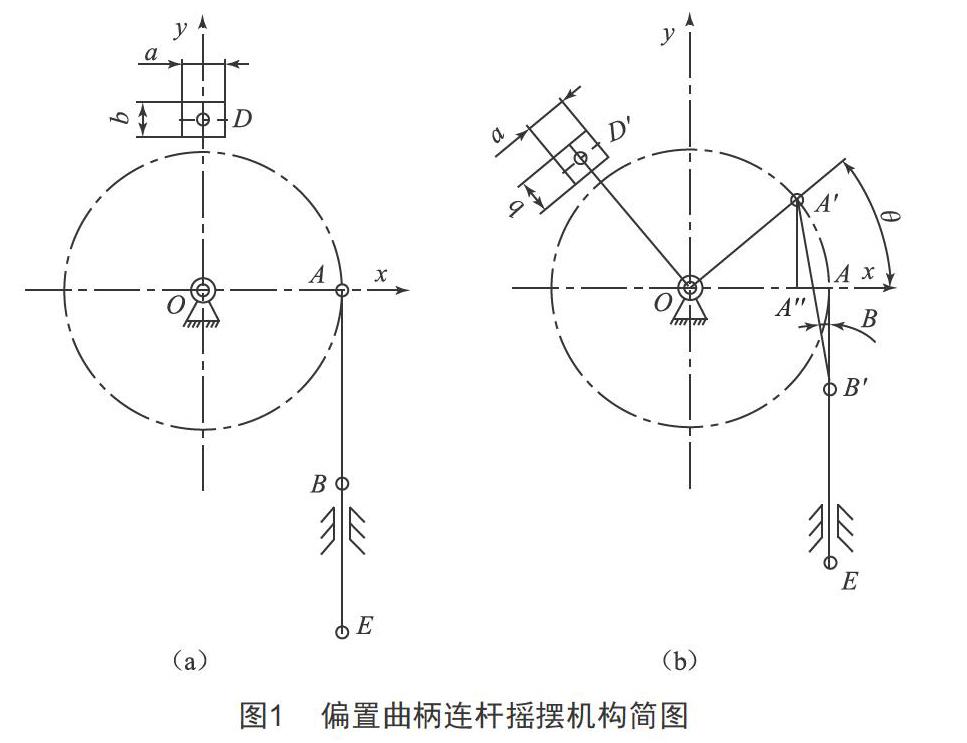
图1为偏置曲柄连杆摇摆机构简图，曲柄OA的长为R1，质量为m1;中心转轴是半径为R2、长为L1、质量为m2的圆轴;杆OD的长为R3，质量为m3;在OD杆的顶端固连一个质量为m4、长为a、宽为b的长方体;滑杆AB长为L，质量不计，滑杆AB在设计过程中要求L/LA″A≥4;BE杆在滑槽内沿Y轴做上下运动，质量不计，角度θ的工作范围为-10°～10°。长为a、宽为b的长方体，曲柄OA，杆OD，质量为m2的圆轴固连为一个刚性连接体。图1（a）表示连杆OA在水平位置，连杆OA和AB处于垂直状态;图1（b）表示连杆OA转过一定角度对应的位置状态。

2    偏置曲柄连杆摇摆机构运动分析

2.1    运动方程建立

由于设计需求（图2（a））已经将连杆OA的转动角度限定在-10°～10°，滑杆AB的运动过程是由伺服电机控制，连杆OA的转动角度在-10°～

-8°以及8°～10°这个区间是伺服电机的加减速区间，-8°～8°这个区间是伺服电机的正常工作区间，滑杆BE受到周期性伺服电机的控制做上下运动，为机构提供动力，产生一个周期性的速度变化（图2（b）），在刚性体AOD上也将产生一个周期性的摇摆动作，根据图2（c）行程S与角度θ之间的关系，建立连杆BE的运动方程为：

LA″A=R1（1-cos θ）=Lsin β               （1）

β=arcsinsin2                        （2）

S=L+R1sin θ-=L+R1sin θ-   （3）

∵已知条件-10°≤θ≤10°，可知：（1-cos θ）≈0。

∴                                S≈R1sin θ                               （4）

公式（4）反映了连杆BE的运动矢量与角度之间的关系，两边分别对时间求导可以得到连杆BE的线速度以及连杆OA绕O点转动的角速度。对角度二次求导可以导出角加速度参数，这样就可以利用这些参数计算出各个零部件的运动转矩。

2.2    曲柄OA以转轴O旋转的角速度及角加速度

对公式（4）两边对时间求导，可以得到滑杆BE的运动线速度：

v==R1cos θ          （5）

曲柄OA以旋转基点O旋转的角速度为：

ω=            （6）

将公式（6）代入公式（5）可以得到：

v=ωR1cos θ         （7）

由公式（7）得到：

ω=               （8）

对公式（8）两边对时间求导得到曲柄OA以旋转基点O旋转角加速度：

?=ω′=

′==    （9）

将公式（8）代入公式（9）得到：

?=     （10）

3    偏置曲柄连杆摇摆机构受力分析

刚性连接体AOD围绕支撑点O做往复旋转运动，会根据速度的变化产生角加速度，由于自身有质量又会产生转动惯量，就会产生旋转扭矩。刚性连接体AOD的受力如图3（a）所示，连杆AB的受力如图3（b）所示，滑杆BE的受力如图3（c）所示。为便于设计工作的计算，连杆AB和滑杆BE的质量可以忽略不计，这样只要计算出刚性连接体AOD的转动惯量，就可以通过围绕O点的力矩的平衡原理计算出力F。

3.1    转动惯量计算

对m1、m2、m3、m4对应的J1、J2、J3、J4的转动惯量计算：

J1=                                （11）

J2=                                 （12）

J3=                                （13）

J4=+m4R32=         （14）

3.2    计算BE杆受到Y轴方向上的作用力F

因为围绕O点的各个力矩的矢量∑M=0，所以通过建立方程可以计算出作用A点的作用力FA，如图3（a）所示。

（J1+J2+J3+J4）α++m2g×0-

-m4gR3sin θ-FAR1=0    （15）

将公式（11）（12）（13）（14）代入到公式（15）中，得到：

FA=

+

+

+

·

+-

-m4           （16）

∵在图3（a）中：

F′cos （θ-β）=FA           （17）

∵在圖3（c）中：

F′cos β=F   （18）

∵滑杆AB在设计过程中通过作图法要求AB杆的长度L/LA″A≥4：

∴                                           β≈0°         （19）

通过公式（17）（18）（19）可以推导出：

F=     （20）

将公式（16）代入公式（20），得到：

F=

+

+

+

·

+-

-m4                 （21）

对公式（21）分析可以知道外部需要提供力F与各个参数之间的关系，运动构件的质量、外形尺寸、连杆OA与水平轴X之间的夹角、滑杆的运行速度v等越大，需要的力F越大。通过上面的分析可知，在设计过程中要尽量减小各个构件的质量与外形尺寸，用较小的夹角来满足运动需求，只有这样设计出来的运动架构才能以较小的力满足使用要求，达到环保、节能、高效的目标。

4    结语

偏置曲柄连杆摇摆机构在实际生产生活中被广泛运用，通过对偏置曲柄连杆摇摆机构的运动分析及受力分析，我们知晓了偏置曲柄连杆摇摆机构是如何实际工作的，对后续设计有很大的参考意义，使得进一步优化设计有了依据，做到了在提高产品质量和技术性能方面有据可依。

在实际工作中需要充分利用经济、技术、生产等各类原理知识，使偏置曲柄连杆摇摆机构的设计工作更加优化，充分利用各种有利因素，不断对产品进行整合创新，使其满足设计使用功能的需求。

[参考文献]

[1] 成大先.机械设计手册[M].5版.北京：化学工业出版社，2008.

收稿日期：2020-04-01

作者简介：徐智（1971—），男，江苏人，工程师，研究方向：食品机械设计。