同步调相机的小干扰运行稳定分析

摘 要：为精确确定同步调相机运行极限，提出了一种在稳定极限约束条件下计算同步调相机稳定极限的方法。该方法运用原始模型对小干扰情况下同步调相机进行建模，得出对应的小干扰线性化模型，进而实现运行极限的计算。仿真结果表明，该方法可以准确计算出稳定运行极限，给实际同步调相机运行提供技术依据。

关键词：同步调相机;海佛容-飞利蒲斯;运行极限

0    引言

随着新能源接入电网的容量不断增大，其大规模、远距离输送成为电网需要解决的问题。实践中为解决此问题，我国大规模建造了直流输电系统。传统直流输电系统一般配置交流滤波器进行无功补偿，然而，直流闭锁后无功迅速过剩，交流滤波器无法迅速切除，将导致严重的过电压，所以提出采用同步调相机来解决直流闭锁后的电压、无功过剩问题。

目前，国内已对同步调相机展开了深入研究，文献[1]研究了同步调相机的控制和运行特性，为其他研究提供了模型基礎。文献[2]研究了同步调相机自动电压控制策略对华东电网稳定运行的影响。文献[3]研究了同步调相机对直流闭锁后的电压支撑作用。上述文献针对同步调相机和电网交互作用作出了深刻研究，为同步调相机实际运行提供了更多经验，但这些文献均未从稳定极限约束的角度去分析同步调相机的运行极限。本文在前人研究的基础上，为准确计算同步调相机下的运行范围，使同步发电机在运行时保持较好的稳定性，推导了同步调相机的模型，通过特征值分析方法给出自动电压控制模式下调相机稳定的约束条件，然后进行仿真建模，对理论推导进行验证，仿真结果表明该方法可以准确计算同步调相机的运行范围。

1    初值计算

建立单机系统无穷大模型时，需要首先确定初值的计算方法，本节介绍同步调相机的初值计算方法，本文计算采用的单位除特别说明的情况外，均为标幺值。

假设同步调相机处于自动电压控制模式，已知量为无功功率Q、发电机有功功率P，根据上述两个电气量求解其他状态量。

同步调相机有功功率很小，同时可以认为功角近似为0，可以根据式（1）计算出有功为：

P=sin δ+sin 2δ         （1）

式中，Eq′为q轴暂态电动势;U为母线电压;xds′=xd′+xs，xd′为发电机d轴暂态同步电抗，xs为变压器和发电机送出线路电抗和;xqs′=xq′+xs，xq′为发电机q轴暂态同步电抗。

由于δ近似为0，可认为sin δ≈δ，sin 2δ≈2δ，则式（1）可以近似改写为：

P=δ+U2δ          （2）

同步调相机的无功表达式Q可以近似写为：

Q=Uqid-Udiq       （3）

式中，Uq为机端电压q轴分量;Ud为机端电压d轴分量;id为机端电流d轴分量;iq为机端电流q轴分量。

由于δ近似为0，可认为：

Uq=Ut

Ud=0                   （4）

综合式（3）和式（4）可以将无功功率表达式改写为：

Q=Utid          （5）

q轴暂态电动势表达式为Eq′：

Eq′=U+xds′id              （6）

将式（5）代入式（6）中可以得到：

Eq′=U+xds′Q/Ut         （7）

而机端电压Ut和母线电压U的关系为：

Ut=U+xsid          （8）

将式（8）代入式（7）中可得：

Eq′=U+xds′Q/（U+xsid）      （9）

将式（9）代入式（2）中可得：

P=δ+U2δ   （10）

机端功率P的表达式为：

P≈Ut δid≈（U+xsid）δid          （11）

根据式（11）可以计算出id的表达式：

id=       （12）

将式（12）代入式（10）中可以得出功角和有功关系：

P=δ+U2δ   （13）

2    海佛容-飞利蒲斯模型

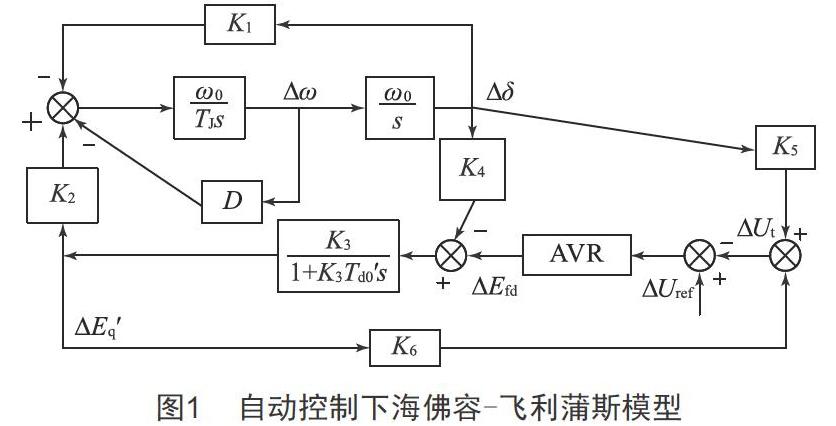
根据上节计算出同步调相机初值后，根据初值可得自动电压控制模式下的海佛容-飞利蒲斯模型。

自动控制模式的海佛容-飞利蒲斯模型中，K1～K6参数具体表达式请参考文献[4]。计算得出K1～K6，可以画出自动电压控制模式下的海佛容-飞利蒲斯模型的控制框图，对应形式如图1所示。

3    仿真研究

为了研究本文提出算法的有效性，下面以一台300 MW调相机为例进行分析。发电机参数如下：xd=1.3，xd′=0.296，xd″=

0.234，xq=1.474，xq′=0.243，xq″=0.234，xs=0.3，TJ=6.4，Td0′=6.5，D=0.2，额定机端电压UN=20 kV。

3.1    工況对调相机稳定的影响

调相机处于自动控制模式下，研究无功和稳定性之间的关系对于运行至关重要。

计算每种有功和无功运行范围下海佛容-飞利蒲斯模型中最弱阻尼，提取出每种工况下的特征值实部，得出每种运行工况下的运行稳定曲线，对应等高线如图2所示。

从图2可以看出，随着有功的增加，阻尼在不断增强;而对于无功变化的趋势，阻尼最强对应在P=0.02 p.u.、Q=-0.5 p.u.附近，超出Q=-0.5 p.u.范围外，调相机的阻尼迅速变弱，但最弱阻尼在-0.05 p.u.附近。

3.2    电力系统稳定器对调相机稳定的影响

在图1中加入电力系统稳定器，计算每种有功运行范围内对应无功，提取出每种工况下的特征值最大实部，得出每种运行工况下的运行稳定曲线，对应等高线如图3所示。

从图3可以看出，加入电力系统稳定器后，最弱阻尼与有功和无功变化规律基本和电力系统稳定器退出时一致。与图2相比，加入电力系统稳定器之后，特征值最大实部分布与退出电力系统稳定器相比更为均匀，虽然在P=0.02 p.u.、Q=-0.05 p.u.时没出现最强阻尼极值点，但在边缘运行区域，阻尼也明显增强。

3.3    放大倍数对稳定的影响

为研究放大倍数KA对自动电压控制模式下发电机稳定性的影响，选取不同的放大倍数KA，计算每一种放大倍数下的特征值最大实部，KA=250对应曲线如图4所示。

图2为KA=200时的特征值最大虚部，对比图2和图4，KA=200时的特征值最大虚部略强于KA=250，说明合理的放大倍数对于维持调相机的稳定是有利的，过大的放大倍数对调相机的阻尼稳定反而不利。

4    结论

本文应用海佛容-飞利蒲斯模型计算同步调相机的稳定极限，为调相机运行提供了技术依据。与以往工作相比，本文的创新点主要体现在：（1）研究同步调相机的稳定分布规律，调相机在特定无功出力情况下最为稳定，超出该范围，阻尼在不断减弱。（2）电力系统稳定器对调相机稳定起着重要作用，电力系统稳定器的加入使得调相机的阻尼分布更为稳定，改善了调相机的稳定性。

[参考文献]

[1] 赵国炫，李辉，鲁文军，等.调相机运行特性和控制策略综述[J].湖南电力，2019，39（3）：43-49.

[2] 巩伟峥，肖洋，夏潮，等.华东电网调相机AVC控制策略研究[J/OL].电网技术：1-10（2020-02-25）[2020-03-28].https：//

kns.cnki.net/KCMS/detail/11.2410.TM.20200225.0831.

001.html.

[3] 李志强，种芝艺，黄金军.快速动态响应同步调相机动态无功特性试验验证[J].中国电机工程学报，2019，39（23）：6877-6885.

[4] 刘取.电力系统稳定性及发电机励磁控制[M].北京：中国电力出版社，2007.

收稿日期：2020-03-30

作者简介：王鹏（1987—），男，黑龙江哈尔滨人，工程师，研究方向：电力系统继电保护。