转化思想在小学数学教学中的渗透

沈骏杰

【摘 要】 转化是一种重要的数学思想，运用转化思想能将问题化繁为简、化难为易。在数学教学中渗透转化思想，需要教师研读教材，理解转化思想的本质;需要教师做实教学过程，逐步渗透数学思想的内涵;需要教师注重实践，为学生构建自主创新的平台，深化转化思想，体会转化思想的奥妙。

【关键词】 转化;研读教材;过程;实践

小学数学要传授的不仅是数学知识本身，而且要让学生在学习过程中理解、掌握一些数学思想。转化是一种重要的数学思想，通过寻找新、舊知识之间的本质联系，将一些难以直接解决的问题变为易于解决的问题，这就是转化思想。本文就以《解决问题的策略——转化》一课为例，分析怎样在小学数学教学中渗透转化思想。

一、研读教材，理解转化思想的本质

如何研读教材、分析教材、把握教材，抓准教学重点，挖掘出简单文字、图片背后的数学思想是提高教学效果的前提;如何把数学教材中的数学思想渗透到教学中去，是数学老师应该思考的问题。

学生的内在需求是学习新知、解决问题的源动力，要产生需求就少不了课程的导入。导入是课堂教学的一个重要组成部分，一个精彩的、睿智的导入能迅速集中学生的注意力。因此教师要挖掘合理的、有趣的素材，激发学生获得新知的欲望。

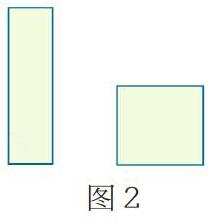
在本课的导入部分，我设计了一个小游戏“比比谁的眼力好”：依次出示三组图形（如下图），比较每组图形的面积大小，看谁看得又准又快。我先出示图1，不到一秒，全班同学异口同声地说右边图形面积大。接着我出示图2（不在方格图中比），只有一小部分同学举手并且结果不一，有位同学认为一样大的同时说出了理由：放到方格图中就能快速算出两个一样大了。最后，我出示图3，基本没人能快速判断，我问学生：“哪个图形难倒你了？”学生说第二个图形不认识，不会算，自然而然地想办法去转化。

图1 图2 图3

在此之前，我尝试过在一个小故事导入后让学生直接比较书上例1两个不规则图形的面积，因为两个图形摆得比较整齐，有学生一眼就看出两个图形一样大，学生的注意力一直在怎么比上，而不是在转化上，重点偏移。因此在仔细研读教材后，我把导入部分和例题部分进行了改编整合，设计了如上一个“比眼力”游戏，一是通过竞赛的方式调动了学生的积极性，集中学生注意力;二是由比较第一组图形一眼就能比出大小，到第二组需要计算面积后才能比，再到第三组直接计算面积遇阻需要转化才能计算，这样一步步地引导学生对转化产生需求，体现转化的优越性;三是这样由易到难的过程符合学生的认知规律，逻辑思维能力也在潜移默化中得到提高。

在例题中我把他们的方法依次板书下来，让他们找找不同方法的共同点——不规则变规则，帮助学生领会转化的思想。在教学中，不仅要让学生比出两个图形的面积大小，也不仅要得出变成长方形的结果，更重要的是凸显出变化过程中的转化思想。

二、做实教学过程，渗透转化思想的内涵

转化思想要在教学过程中逐步渗透。因此，教师要了解学生的学情，设计合理的教学过程。一是让学生经历由具体到抽象的过程，体味转化思想;二是加强知识联系，感受转化思想价值。

1.设计由具体到抽象的过程，渗透转化思想

在本课中，上面图3中比较两个图形的面积大小，让学生用自己的方法来解决右边不规则图形的面积。交流时，学生1：“把左右两边的半圆割掉，补到上面去，原来的花瓶图就变成一个长方形，6×4是24。”学生2：把上面的部分切成两部分，补到下面，这样原来的图形就变成一个“横”的长方形，8×3也是24。”我一边听学生的介绍，一边板书：原来的花瓶图→长方形;原来的图形→“横”的长方形，接着我让学生观察板书：“这2种方法有什么相同的地方？”通过交流，学生很快就能意识到，这两种都是由不规则的图形变成规则的图形，由未知变成已知，由复杂变简单，这就是转化的思想。

通过上述过程，首先让学生经历解决不规则图形面积的具体过程，其次让学生去观察不同方法之间的共同点，归纳出都是不规则图形变成规则图形，最后由归纳的结论抽象出“转化”的思想。不仅要学生比出两个图形的面积大小，得出变成长方形的结果，更重要的是让学生在过程中体会到转化的思想，理解转化的本质。

2.加强知识联系，感受转化思想价值。

教师要加强知识之间的联系，组织学生适时地回顾反思，在学习本课之前，我安排了一个问题：同学们，你们还记得我们以前在解决哪些问题时也用到过转化的策略？学生列举了图形和计算中的转化，我又补充了生活中的转化：测量树叶周长、“曹冲称象”、测量灯泡体积等，结合生活实际，加强知识间的联系，进一步体会转化思想的价值。

三、注重实践，创设深化思想的活动。

“一个人，只有在实践中运用能力，才能知道自己的能力。”在实践活动中获得知识、运用知识能帮助学生更好地领悟转化思想。因此，我们要努力创设深化转化思想的实践活动，让学生感受转化思想的魅力。在本课中最后一个环节，自主设计图形，在实践中深化转化思想。我突破常规的练习思路，尝试让学生自己设计能够用转化思想来解决的图形问题。学生在短短8分钟之内设计了许多形状各异的不规则图形，并能用转化思想来解决面积或周长问题。这样的一个设计活动，不仅仅是画一个简单的图形，更是要逆向思考，让学生首先在脑中勾画出一个规则的图形，再结合自己的个性加工，最终形成一个符合转化要求的不规则图形，既渗透了转化思想，还在无形中锻炼了学生创新能力和逆向思维能力。

转化是数学上一种重要的数学思想，运用转化思想能将问题化繁为简、化难为易。我们教师在教学中要研读教材，认真做实教学过程，以学生为主体，引导学生抓住数学知识的本质，用转化的思想去解决更多的数学问题。

【参考文献】

[1]刘长福.在小学数学“空间与图形”教学中渗透转化思想[J].科学咨询，2014（2）：77-78.

[2]蒲春燕，数学思想方法的教学价值及实践途径——以转化思想为例[J].教育科学论坛，2014（5）：26-28.

[3]曾玉梅.关于小学生数学计算能力的培养与研究[J].小学生，2016（02）.