摩擦副曲率半径对织构动压润滑性能的影响

廖文玲

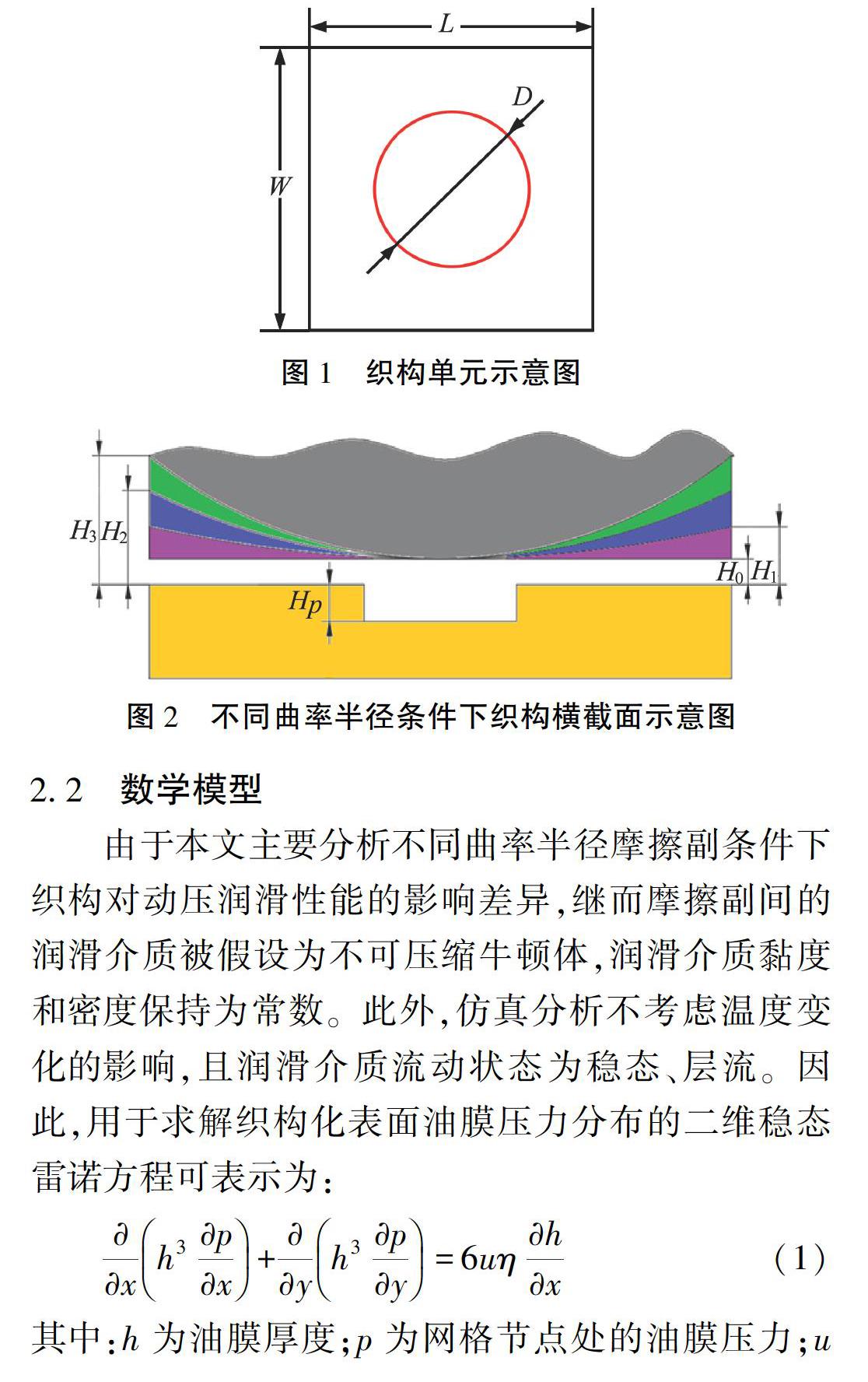
摘要：基于雷诺方程建立不同曲率半径织构化摩擦副动压润滑理论模型，采用有限差分和高斯赛德尔迭代法对模型进行求解，研究不同摩擦副曲率半径条件下表面织构对动压润滑性能的影响差异。数值仿真分析结果表明：织构化曲面摩擦副流体动压尽管由曲面摩擦副流体动压和织构微流体动压组合而成，而两部分之间的干涉将对摩擦副的动压润滑效果带来负面影响，且摩擦副曲率半径越小，干涉越明显;而摩擦副曲率半径对织构分布和最优织构深度的影响则需要对两参数综合分析。

关键词：不同曲率摩擦副;表面织构;动压润滑性能

中图分类号：T117.2 文献标志码：A

文章编号：2095-5383（2020）02-0001-08

Abstract： The aim of the present research was to investigate the influence of curvature radius of friction pair on hydrodynamic lubrication performance of texture. For this purpose， the hydrodynamic lubrication theoretical model of textured surface with different radius of curvature was established based on the Reynolds equation， and finite difference algorithm and Gauss-Seidel iterative method were used as numerical approach. The results of numerical simulation show that although the dynamic pressure of the friction pair of the texture surface is composed of the dynamic pressure of the hook surface friction pair and the dynamic pressure of the texture micro-fluid， the interference between the two parts will have a negative impact on the hydrodynamic lubrication performance the friction pair， and the smaller the radius of curvature of the friction pair， the more obvious the interference. Besides， the influence of curvature radius of friction pair on texture distribution and optimal texture depth requires a comprehensive analysis of the two parameters.

Keywords：friction pairs with different curvature; surface texture; hydrodynamic lubrication performance

1 研究背景

在機械产品设计过程中，可靠性、工作性能和使用寿命是需要考虑的主要因素。因此，提高机械产品的工作性能和使用寿命对提高其市场竞争力具有重要的意义，而各机械零部件配合表面的摩擦磨损又是影响机械系统工作性能和使用寿命的重要因素。针对如何提高摩擦副表面的润滑及摩擦学性能，研究人员从多方面进行了探索和分析，在一定程度上有效改善了机械零件的工作性能和使用寿命[1-3]。近年来，研究人员结合自然界中生物表皮特殊结构具有良好减磨效果这一现象，提出了将仿生表面织构技术应用于机械系统摩擦副表面，以探索新的机械摩擦磨损有效改善方法。通过大量的仿真和实验研究发现，基于不同润滑状态下的作用机理：全油膜润滑状态下产生微流体动压[4]、混合润滑状态下补充润滑介质[5]、干摩擦状态下捕获磨屑，仿生表面织构的存在能够有效改善相对运动表面的摩擦学性能[6]，且不同工况下存在最优织构参数使得织构的润滑减磨效果最佳。针对全油膜润滑条件下，织构参数的优化设计，研究人员开展了大量的研究工作，并取得了一系列的研究成果。对于曲面摩擦副，Kango等[7]建立织构化动压滑动轴承润滑模型，分析织构分布方式的影响，结果指出，织构分布于油膜压力收敛区域时相比于光滑轴承和全织构化轴承润滑性能更好。Gadeschi等[8]通过建立织构化活塞环动压润滑理论模型，分析了织构密度、织构深度和织构分布方式对活塞环动压润滑性能的影响，结果指出，最大无量纲化表面承载力对应的最优无量纲化深度分别为1.866和2.0、无量纲织构长度为2.55、织构面积比为60%。Brizmer等[9]分析结果表明，轴承偏心率小于0.3时，全尺寸分布及部分区域分布织构均能提高轴承的润滑性能，但更大偏心率时织构对轴承润滑性能的提高并无明显效果。Meng等[10]通过建立复合织构化滑动轴承几何模型，研究了复合凹坑织构对滑动轴承动压润滑性能的影响。仿真研究结果表明，相比于简单凹坑织构，由于复合织构的二次流体动压效应，复合表面织构对滑动轴承动压润滑性能的提升更优。而对于平面相对运动摩擦副，Shi等[11]建立了椭圆形、圆形、封闭性沟槽形和穿插式沟槽形织构机械密封动压润滑理论模型，分析了4种不同类型织构对机械密封表面润滑性能的影响，结果表明，织构面积比小于10%时，微沟槽型织构对表面承载力和油膜刚度的提升优于微凹坑型织构，而织构面积比大于10%时，则椭圆形织构表面表现出最优承载性能。Wang等[12]建立了织构化推力滑动轴承动压润滑理论模型，分析表面织构对推力轴承承载性能的影响，研究结果指出，存在最优织构参数获得最优织构化推力轴承承载力，织构深度太深或太浅都将对表面承载力有消极影响。陈源等[13]在建立不同参数的织构化螺旋沟槽干气密封几何模型基础上，分析了高速高压条件下螺旋沟槽结构参数对气膜动压特性的影响，计算结果表明，不同沟槽结构对气膜动态特性有不同的影响，当沟槽台宽比为0.9～1.5、沟槽坝比为1.8～2.4、沟槽螺旋角为18° ～24° 、沟槽深度比为6～8 μm时，螺旋沟槽干气密封气膜具有良好的动态特性。因此，根据国内外的研究结果可以发现，无论平面相对运动摩擦副还是曲面相对运动摩擦副，表面织构的存在都能有效改善摩擦副的动压润滑性能。但是，对于两种摩擦副，研究人员基本采用其中一种接触运动形式，未对两种运动摩擦副（平面相对运动和曲面相对运动摩擦副）的差异进行对比分析，探索其中的差异性。

因此，本文通过设计平面与不同曲率圆弧相对运动的几何模型（平面曲率为无限大），并基于雷诺方程建立织构化动压润滑理论模型，采用有限差分法对方程进行求解，研究摩擦副曲率半径变化时织构对动压润滑性能的影响差异，为探索适用性更广的织构优化设计方法奠定基础。

3 结果与讨论

3.1 相同条件下曲率半径的影响

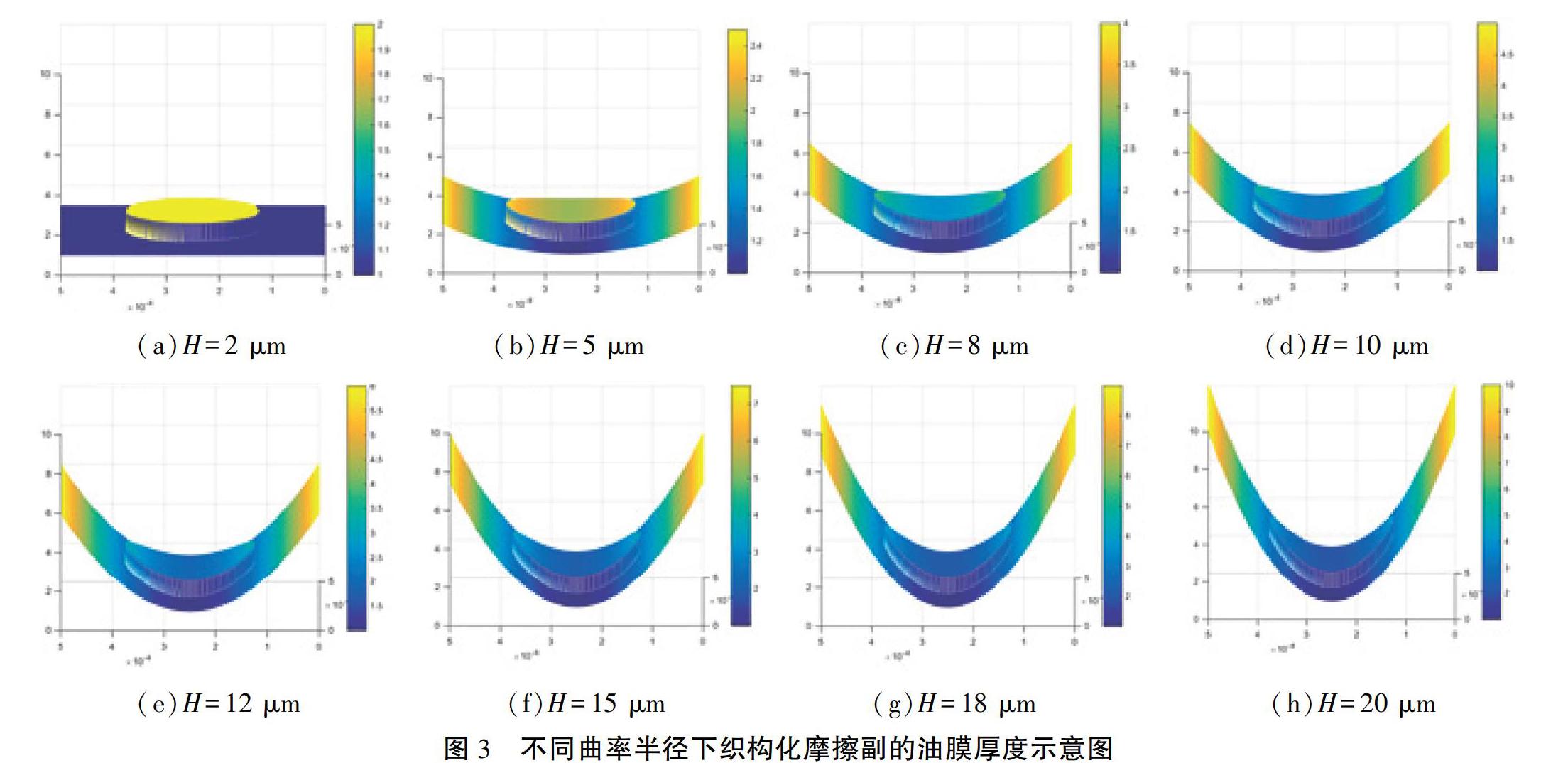
为了研究摩擦副曲率半径对织构动压润滑性能的影响，本文将织构加工于织构单元中间，对应的不同曲率半径下摩擦副表面的油膜厚度如图3所示。摩擦副曲率半径变化时对表面承载力的影响规律，如图4所示，当摩擦副表面未加工织构时（HP=0 μm），随曲率半径的减小，表面承载力也基本呈现线性递减的变化趋势，因此，摩擦副曲率半径越大，其动压润滑性能将越好。而当摩擦副表面加工有圆形凹坑织构时（HP=1～10 μm），从图4中可以看出，在织构深度为1 μm、2 μm和5 μm情况下，表面承载力随曲率半径的减小先快速降低而后递减趋势变缓，即两摩擦副表面均为平面时承载力最大;此外，可以发现，相比于无织构不同曲率摩擦副，织构化摩擦副承载力快速递减时的减小趋势更大、而缓慢递减时的减小趋势则更小。在织构深度为10 μm的情况下，织构化摩擦副表面的承载力随曲率半径的减小则先表现出先增加后减小的变化趋势，曲率半径为10 418.2 μm（对应摩擦副两端的油膜厚度为5 μm）时表面承载力最大;且随摩擦副曲率半径的减小，织构深度为5 μm和10 μm时表面承载力变化曲线逐渐重合，即2种织构深度下，摩擦副曲率半径对织构动压润滑性能的影响规律基本相同。

为了进一步探索摩擦副曲率半径对动压润滑性能的影响机理，无织构情况下，摩擦副曲率半径对油膜压力分布的影响，如图5所示，随摩擦副曲率半径的逐渐减小，摩擦副表面的最大动压油膜和动压油膜分布区域呈现逐渐减小的变化趋势，即摩擦副曲率半径越小，最大油膜动压值和动压油膜分布区域均越小，很好地解释了图4中无织构情况下摩擦副曲率半径对承载力的影响规律。织构深度为2 μm时，摩擦副曲率半径对表面油膜动压分布的影响，如图6所示。从图6（a）中可看出，当曲率半径无限大（即两摩擦副均为平面）时，由于表面织构的存在，在摩擦副表面将产生流体动压润滑的效果，且流体动压区域主要分布在织构出口端;而当摩擦副曲率半径减小时，从图6（b）～6（h）可知，摩擦副表面的动压油膜将由两部分组成，分别为曲面摩擦副产生的流体动压和织构产生的流体动压，且从图中可以看出，表面织构入口端空化效應的存在将削弱曲面摩擦副流体动压效果，而曲面摩擦副的存在也将削弱织构出口端的流体动压效果，导致两部分最大油膜动压大大减小。取摩擦副表面中线上的油膜压力进行对比，结果如图7所示，也可以发现，当摩擦副曲率半径无限大时（两摩擦副均为平面），摩擦副中线上的最大油膜动压均大于摩擦副为曲面的情况、且织构深度越小越明。而曲面摩擦副尽管能产生额外的动压油膜，但相比而言油膜动压数值较小;随摩擦副曲率半径的减小，额外的油膜动压也将越来越小。因此，图5～7中动压油膜分布规律和大小关系很好的解释了图4中摩擦副曲率半径对表面承载力的影响规律。

3.2 曲率半径对织构分布位置的影响

为了分析摩擦副曲率半径对织构分布位置的影响，本文分别选择了5种不同分布位置情况，不同分布位置情况下的油膜厚度，如图8所示。同一摩擦副曲率情况下，随织构从最左边到最右边分布时表面承载力的对比，如图9所示，可知在4种不同织构深度条件下，当摩擦副为平面时，最织构从最左边分布到最右边分布，摩擦副表面的承载力呈现出逐渐减小的变化趋势，即织构分布在左边（润滑介质入口处）;而当摩擦副去曲面时，承载力则表现出波动的变化规律，织构深度为1 μm是先减小后增加、织构深度为5～10 μm是先增减后减小而后再增减的变化。此外，从图9也可以看出，在各织构深度下，对于任意曲面摩擦副，织构分布于摩擦副中间时表面承载力最小，即动压润滑性能最差;但当织构深度小于或等于最小油膜厚度时，曲面摩擦副织构分布在摩擦副左边（润滑介质入口处）时其动压润滑性能较好，而织构深度大于最小油膜厚度时则织构分布在摩擦副右边（润滑介质出口处）逐渐展示出优越性。

相同摩擦副曲率条件下，当织构深度等于最小油膜厚度2 μm时，织构不同分布位置对摩擦副中线油膜压力的影响，如图10所示。从图10（a）中可以看出，当两摩擦副均为平面时，中线上的油膜压力按织构从左到右分布一次下降;而图10（b）和图10（c）中则可发现，摩擦副为曲面时，在不同曲率下，中线上的油膜压力基本呈现为：左边>右边>中间，因此，中线上油膜压力的大小关系与图9中承载力的变化规律完全吻合。则描述了织构深度为10 μm时，不同摩擦副曲率半径条件下，织构分布对中线上油膜压力影响的对比，如图11所示，不同曲率条件下，中线上油膜压力在不同织构分布时的大小关系与图9中表面承载力的大小规律也同样完全吻合。

所以，综上可知，当摩擦副为平面时，织构位于润滑介质入口处其动压润滑性能最优，而摩擦副为曲面时织构分布的影响规律则与织构的深度有关，但与曲面摩擦副的曲率半径无关。

3.3 曲率半径对最优织构深度的影响

图12描述了不同摩擦副曲率半径条件下，织构深度对表面承载力的影响。从图12（a）和图12（b）中可以看出，当表面织构分布在左边（润滑介质入口端）或中间时，摩擦副曲率半径对表面承载力的影响规律基本相同，即织构深度小于或等于最小摩擦副间隙时表面承载力更大，而织构深度大于最小摩擦副间隙时则承载力偏小。从图12（d）和图12（e）中可知，当织构分布在右边（润滑介质出口处）时，织构深度的影响在两摩擦副面均为平面时差异较大，而摩擦副为曲面时则不同曲率半径条件下织构深度基本无影响。因此，对于不同曲率半径的摩擦副，曲率半径对最优织构深度的影响与织构分布有关，分布在左侧时织构深度小于或等于最小摩擦副间隙情况下的动压润滑性能更好，而分布在右侧则仅在两摩擦面均为平面时织构深度影响较大，摩擦面为曲面基本无影响。

4 结论

基于雷诺方程建立不同曲率织构化摩擦副动压润滑理论模型，并采用有限差分和高斯赛德尔迭代法进行求解，研究摩擦副曲率半径对织构动压润滑性能的影响。数值仿真研究结果可得出以下结论：

1）相比于两平面相对运动摩擦副，织构化曲面摩擦副表面的流体动压尽管由曲面摩擦副流体动压和织构微流体动压两部分构成，但两部分之间的相互干涉作用将大大削弱整体的流体动压效应，且曲面摩擦副曲率半径越小，干涉作用将越明显;

2）摩擦副为平面时，织构位于润滑介质入口处其流体动压效果最好，而摩擦副为曲面时最优织构分布则与织构深度有关，与曲面摩擦副的曲率半径无关;

3）摩擦副曲率半径对最优织构深度的影响与织构分布位置有关;织构位于左侧（润滑介质流入端）或中间时，织构深度小于或等于最小摩擦副间隙情况下的动压润滑性能更好;织构位于右侧（润滑介质流出端）时，仅当两摩擦面为平面时织构深度影响的差异较大，而摩擦副为曲面则基本无影响。

参考文献：

[1]LIU Y H， WANG X K， LIU P X， et al. Modification on the tribological properties of ceramics lubricated by water using fullerenol as a lubricating additive[J]. Science China Technological Sciences， 2012， 55（9）：2656-2661.

[2]FINK J K. Reactive polymers fundamentals and applications： a concise guide to industrial polymers [M]. Amsterdam： Elsevier inc， 2013.

[3]HUANG Z， LI Q， ZHOU Y， et al. Experimental research on the surface strengthening technology of roller cone bit bearing based on the failure analysis[J]. Engineering Failure Analysis， 2013（29）： 12-26.

[4]SHEN X H， TAO G C. Tribological behaviors of two micro textured surfaces generated by vibrating milling under boundary lubricated sliding [J]. The International Journal of Advanced Manufacturing Technology， 2015， 79（9-12）： 1995-2002.

[5]KIM B， CHAE Y H， CHOI H S. Effects of surface texturing on the frictional behavior of cast iron surfaces [J]. Tribology International， 2014（70）： 128-135.

[6]PETTERSSON U， JACOBSON S. Textured surfaces in sliding boundary lubricated contacts-mechanisms， possibilities and limitations[J]. Tribology-Materials， Surfaces & Interfaces， 2007， 1（4）： 181-189.

[7]KANGO S， SHARMA R K， PANDEY R K. Thermal analysis of microtextured journal bearing using non-Newtonian rheology of lubricant and JFO boundary conditions[J]. Tribology International， 2014（69）： 19-29.

[8]GADESCHI G B， BACKHAUS K， KNOLL G. Numerical analysis of laser-textured piston-rings in the hydrodynamic lubrication regime[J]. Journal of Tribology， 2012， 134（4）：041702.

[9]BRIZMER V， KLIGERMAN Y. A laser surface textured journal bearing[J]. Journal of Tribology， 2012， 134（3）： 031702.

[10]MENG F M， ZHANG L， LIU Y， et al. Effect of compound dimple on tribological performances of journal bearing[J]. Tribology International， 2015（91）： 99-110.

[11]SHI L， WANG X， SU X， et al. Comparison of the load-carrying performance of mechanical gas seals textured with microgrooves and microdimples[J]. Journal of Tribology， 2016， 138（2）：88-90.

[12]WANG W， HE Y， ZHAO J， et al. Numerical optimization of the groove texture bottom profile for thrust bearings[J]. Tribology International， 2017（109）： 69-77.

[13]陳源， 彭旭东， 李纪云， 等. 螺旋槽结构参数对干气密封动态特性的影响研究[J]. 摩擦学学报， 2016， 36（4）： 397-405.