XT260卧式冷室压铸机大杠再制造工艺路线优化研究
2020-06-29付悦,杨林,崔晶
付 悦,杨 林,崔 晶
(沈阳工业大学 机械工程学院,辽宁 沈阳 110000)
0 前言
再制造工艺路线优化问题受到众多学者的关注。如:江亚等以再制造能耗、成本、时间等多种因素为优化目标,以修复工艺与参数、资源配置等为约束前提,提出了一种基于遗传-神经网络的混合优化方法[1]。Li等建立了基于gert图的再制造工艺路线模型,并就再制造生产计划和控制策略等方面问题提出了基于混合细胞遗传算法的再制造工艺优化方法[2]。基于此,本文以废旧XT260卧式冷室压铸机大杠为研究对象,以失效特征为切入点,采用遗传算法对其进行再制造工艺路线优化研究。
1 XT260卧式冷室压铸机大杠概况
压铸机大杠结构简单,但其对设备刚性和稳定性有着很大的影响,长螺纹一端装调模螺母连接尾板,短螺纹一端装大杠螺母连接头板。大杠在压铸成型过程中承受巨大的锁模力,且在服役过程中不可避免受工况及外界因素等影响,容易出现磨损、腐蚀等失效形式而影响整机的压铸效果。由于大杠制造周期、加工成本及其本身的结构特点,通常对失效的大杠进行再制造修复后使用。由于废旧大杠有很多不确定因素(如剩余寿命、失效特征等),导致其再制造工艺路线多种多样。修复工艺是再制造的关键环节,选择合适的工艺路线并对其进行优化有利于提高生产效率、降低成本。
XT260卧式冷室压铸机大杠材料为42Cr,新件价格约为3 580元,主要参数信息如图1所示。该大杠再制造工艺路线优化是对每一道工序选择合适的机器与刀具,通过最佳设备组合达到成本与工时最小化的目标。
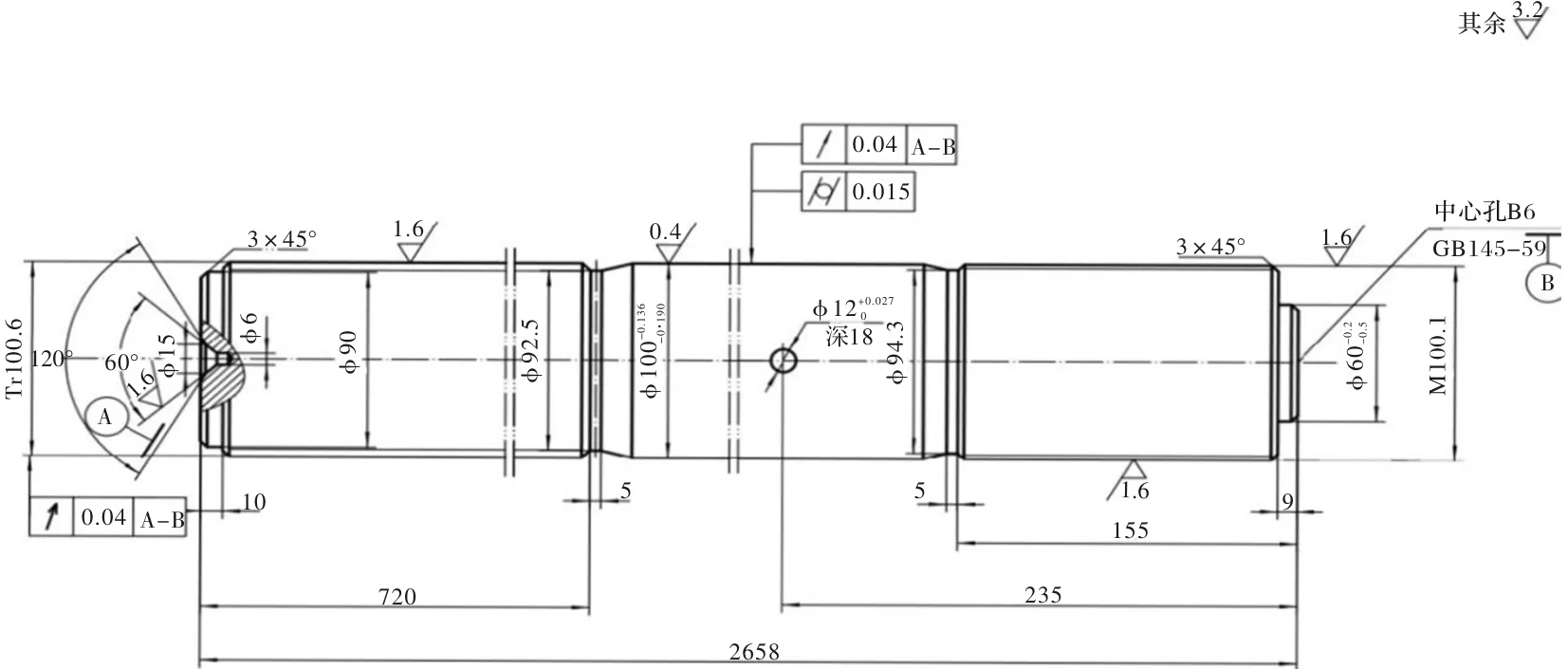
图1 XT260卧式冷室压铸机大杠
2 失效特征分析
2.1 故障树法提取失效特征
故障树法是一种由上往下的演绎式失效分析法,并用专门的符号来表示上、下层次之间的联系与制约[3]。废旧XT260卧式冷室压铸机大杠故障树的建立是从其表面状况追溯到失效特征进而确定失效原因的过程。失效特征有利于选择合适的修复工艺,为设计最佳修复方案提供依据。图2为XT260卧式冷室压铸机大杠的故障树模型,提取的失效特征为:P4、E1、E2、E3、E4、E5、E6,分别表示:变形、长螺纹磨损、表面损伤、短螺纹腐蚀、表面点蚀、长螺纹根部裂纹、局部疲劳裂纹。
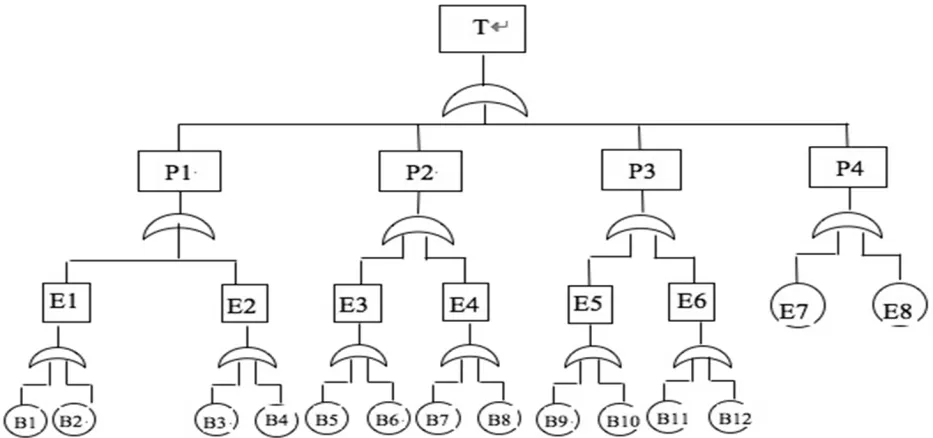
图2 XT260卧式冷室压铸机大杠故障树模型
2.2 损伤量模型获取
损伤部位模型可通过图3获取,在此过程中,配准的两模型对应点间的最大距离即为最大损伤深度,损伤深度决定镀层厚度,影响修复工艺的选择[4]。损伤深度将作为该大杠修复方案生成的主要参考依据。
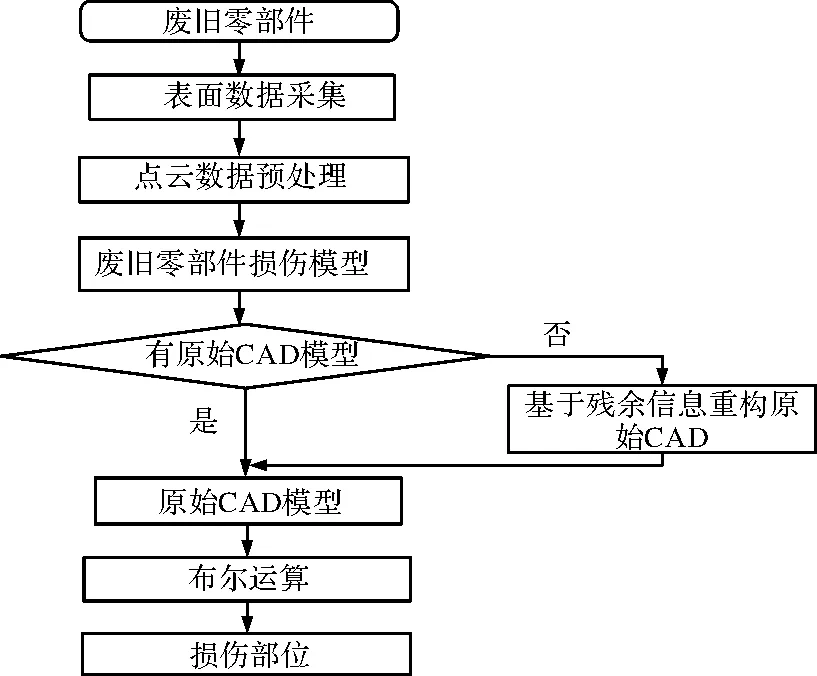
图3 损伤量模型获取流程图
3 基于规则推理的再制造初始方案生成
针对废旧零部件不同的失效形式、损伤程度等,一般会有与之相对应的修复工艺,且两者存在一定的规则。采用规则推理的方法生成废旧XT260卧式冷室压铸机大杠的再制造初始方案如表1所示,其表达形式为if
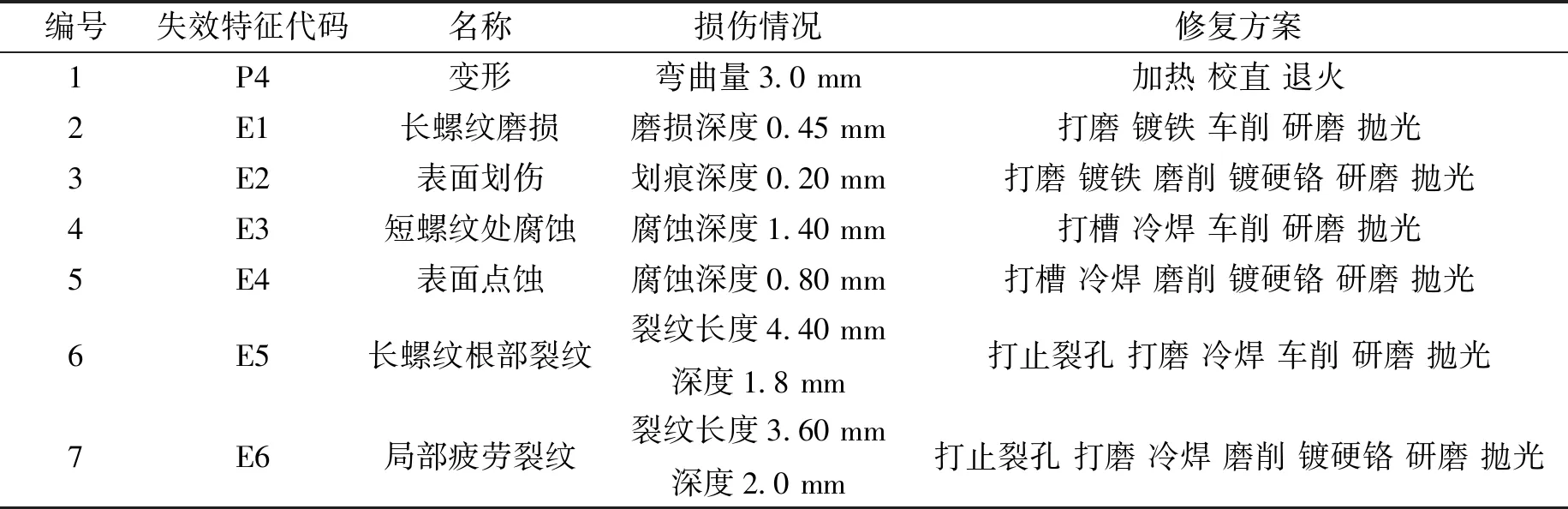
表1 大杠再制造修复方案
if失效部位=长螺纹表面
and失效特征=磨损
and磨损深度<0.5mm
then修复方案为:打磨,镀铁,车削,研磨,抛光
4 压铸机大杠再制造相关设备
压铸机大杠再制造过程中相关设备信息如表2和表3所示,刀具信息如表4所示。
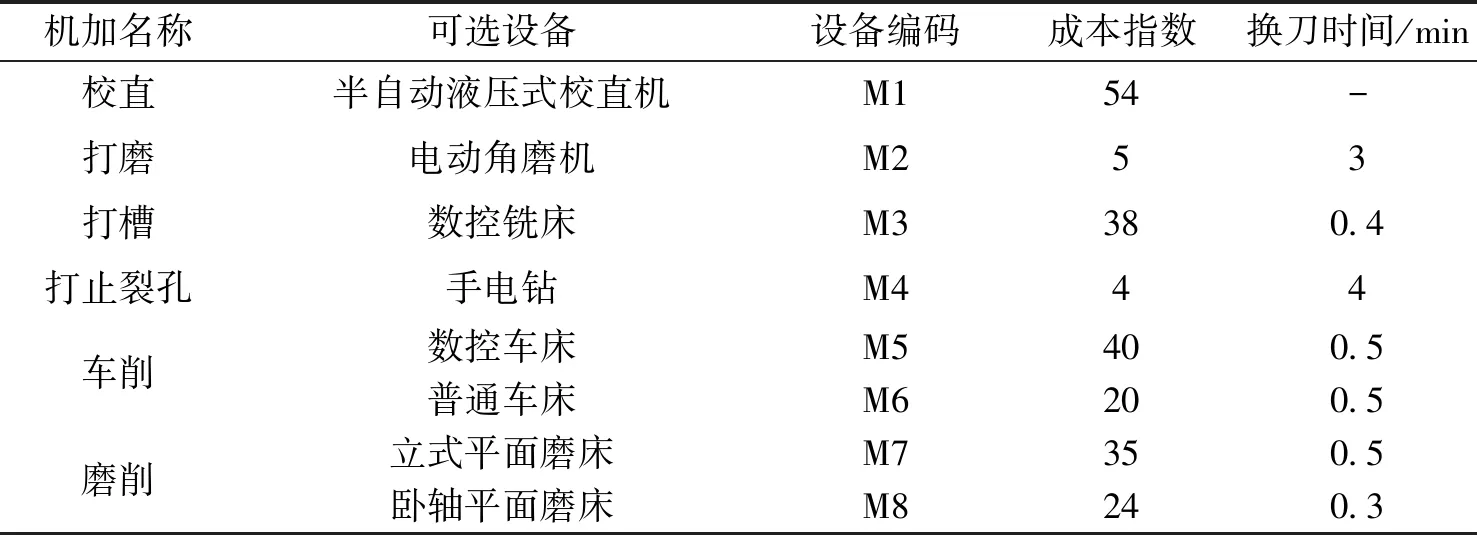
表2 机械加工设备信息
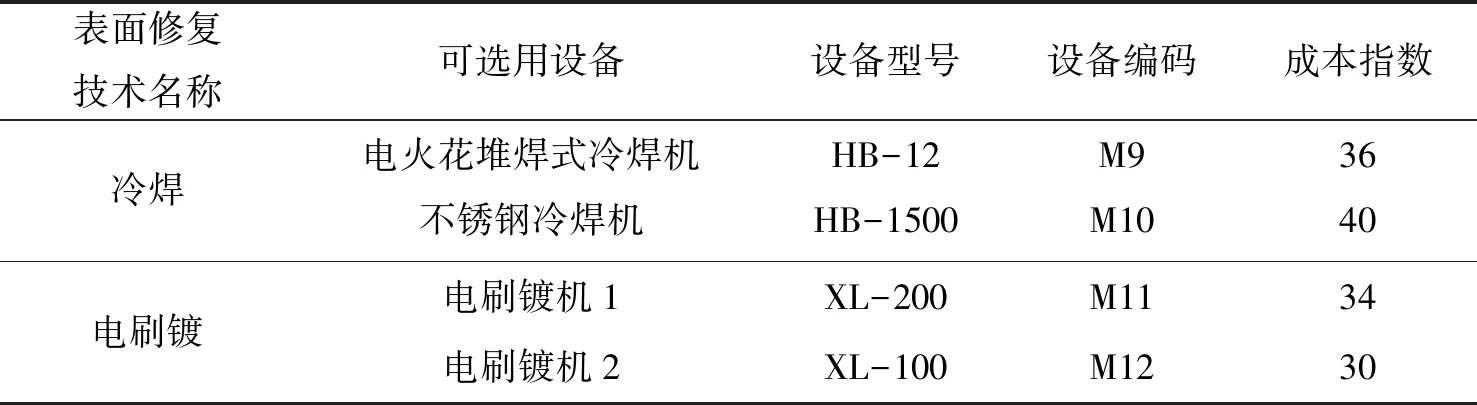
表3 表面修复设备信息
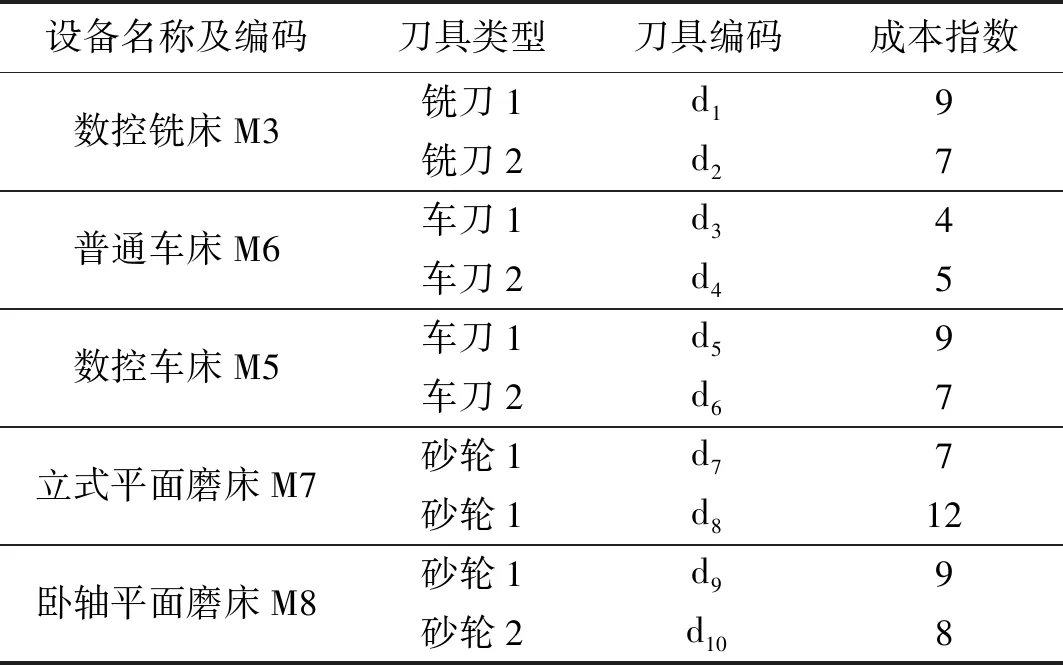
表4 刀具信息
5 基于遗传算法的再制造工艺路线优化求解过程
5.1 约束描述
建立废旧XT260卧式冷室压铸机大杠优化数学模型前,需要对其约束条件进行说明,具体如下:
(1)在优化过程中同一时刻该工件只能在一台机器上加工且不发生中断[5]。
(2)该工件各个失效特征间工序没有先后约束关系,但一个具体失效特征的工序之间有先后约束关系。
(3)不同的失效特征具有相同的优先级。
5.2 构建目标函数
时间是再制造效率的直观体现,费用直接关系到再制造产品的经济性与企业效益。因此在构造大杠再制造优化目标函数时考虑时间和成本两个因素[6]。
5.2.1 再制造时间函数
在不考虑装夹、运输等辅助时间的情况下,大杠的再制造时间函数可表示为表面工程技术加工时间(Tb)与机械加工时间(Tj)之和,即
(1)
式中,n为最大表面修复设备数量;ti为第i台设备运用表面工程技术的加工时间。m为最大机加设备数量;tkq为第k台机加设备切削时间;tkz为第k台机加设备空载时间;tkh为第k台机加设备换刀时间。

(2)
5.2.2 成本函数
大杠再制造时的成本主要考虑人工费(Cr)和设备费(Cs),可表示为
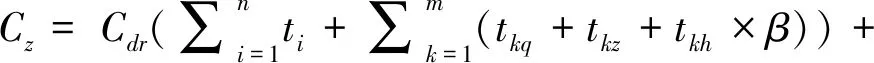
(3)
式中,Ck为第k台设备在单位时间内的成本指数,对于具体规格的设备来说是个定值,Cdr为单位时间与人相关的成本指数,Cdr=30元/时。
5.2.3 目标函数转化
在实际生产中成本与时间两个目标函数往往存在冲突关系,且处理起来十分困难,不易求解。若将其先转换为单目标优化问题再进行求解,会使得整个运算过程更加简单直接,转化后的数学模型可描述为
(4)
式中,w为权重系数,w1=0.35,w2=0.65,其数值通过层次分析法确定。
时间与成本两个目标函数的量纲不同,在运算前统一规范成可以比较的形式。规范后的时间与成本目标函数可表示为
(5)
式中,Tmax、Cmax表示函数最大值,Tmin、Cmin表示函数最小值。
5.3 遗传算法实现过程
(1)编码。编码的方法有很多种,但对于约束优化问题常用的是实数编码法。实数编码法无需特定的编码与解码过程,运算难度降低,执行效率提高,所以大杠再制造工艺路线优化采用实数编码。
(2)适应度函数。大杠再制造工艺路线优化的目标函数总是非负的且是求最小值问题[7],其适应度函数可表示为
(6)
(3)初始种群。一般群体规模在10~200之间,在运行该算法时将其设置为50。逐次以适应度值高的个体为模板并将不同的个体模板组成种群。若达到种群规模则进行下一步操作,否则在滤除的个体中选取适应度值大的来补缺[8]。
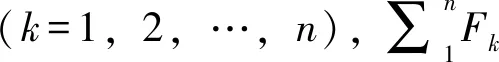
(5)交叉。根据再制造工艺路线优化特点,采用单点交叉操作,减少了不可行解的产生,使得算法效率显著提高。交叉概率一般建议取值范围是0.4~0.99,该算法中将其设置为0.6。
(6)变异。变异概率一般建议取值范围是0.0001~0.1,该算法中将其设置为0.03,运行时根据该变异概率随机的做某一规则的基因突变[10]。
(7)终止。算法迭代到500次时终止运行。
5.4 优化结果
根据初始信息、约束条件及设置参数等,通过matlab来运行该遗传算法得到图4。优化后的单目标函数值为72.54。其再制造成本为72.8元,时间为72.4 min ,最佳设备组合情况如表6所示。
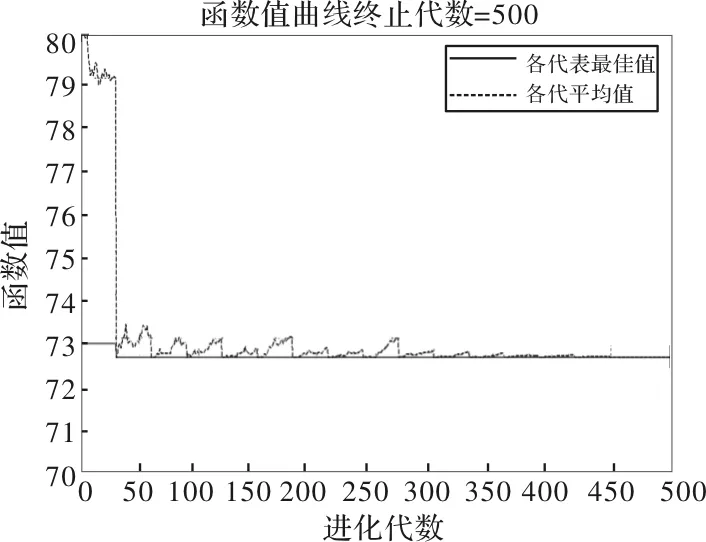
图4 函数值与迭代次数关系图
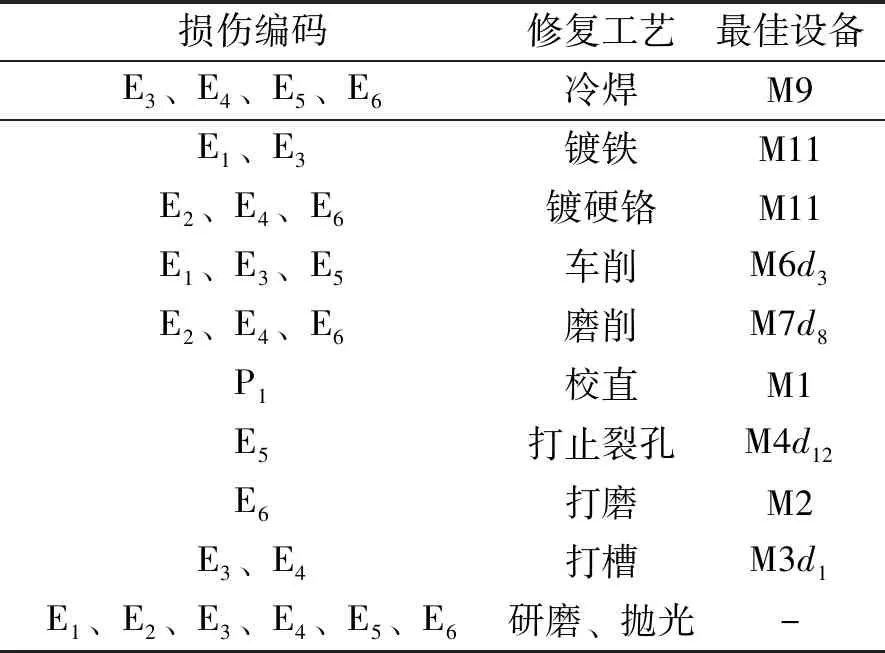
表6 最佳设备组合
6 结论
多数情况下大杠的再制造工艺路线仍由技术人员凭借经验制定,具有强烈的主观性缺乏科学性。因此采用遗传算法对其进行优化研究,得到时间和成本最小化时的设备组合情况,可为车间实际生产提供些许参考。但再制造工艺路线优化是一个动态问题,在应用遗传算法进行求解时,如何对算法中的重要步骤进行改善提高运算效率与准确度仍需进行深入研究。
