引入失效数据的腐蚀管道结构可靠性评价方法

2020-06-29张佩颖虞维超王圣洁

安全与环境工程 2020年3期

张杰，张佩颖，虞维超，刁逢，王圣洁，宫敬

(1.中国石油大学(北京) 油气管道输送安全国家工程实验室,北京 102249;2.中国石油天然气股份有限公司北京油气调控中心，北京 100007)

管道输送是油气资源输送最有效的方式，管道失效数据统计结果表明，管道腐蚀失效占管道失效总量的近30%，是造成管道失效的主要原因之一[1]。为了提高管道的安全运行能力，国内外学者对腐蚀管道的结构可靠性进行了大量研究[2-4]。腐蚀管道结构可靠性评价是评估腐蚀对管道完整性破坏程度的一种有效方法，生产和运行过程中所涉及的不确定性都通过概率方法纳入其中[5-7]。腐蚀管道结构可靠性分析通常基于含腐蚀缺陷管道的极限状态函数，通过建立管道腐蚀缺陷生长模型，采用蒙特卡罗等方法计算管道的失效概率，进而评价管道在全生命周期内的可靠性[8-10]。

建立适当的管道腐蚀缺陷生长模型对腐蚀管道结构可靠性评价的准确性和有效性至关重要：一方面，过高估计管道腐蚀速率会导致对管道进行不必要的检测和维护，造成管道管理成本过高；另一方面，过低估计管道腐蚀速率则会由于未能及时对管道进行预防性维护而导致管道失效，造成严重的后果[11]。管道腐蚀缺陷的生长过程本质上是随机的，包括时间和空间的变异性。时间变异性意味着管道腐蚀缺陷的增长速率会随时间变化，空间变异性意味着不同管道腐蚀缺陷的增长速率不同。文献[12]采用随机过程的方法建立了管道腐蚀缺陷的概率增长模型。

由于设计、制造和运行工况的原因，管道的结构参数、缺陷的尺寸参数之间相互关联，多个腐蚀缺陷的增长相互依赖，在统计意义上均表现出一定程度的相关性[13-16]。张鹏等[14]研究了单个缺陷的尺寸参数之间的相关性对腐蚀管道结构可靠性的影响，但未考虑多个腐蚀缺陷生长过程的相关性；Li等[15]将缺陷之间的相关性视为概率交集进行研究，提出了一种管道腐蚀缺陷的概率增长计算方法，但没有模拟多个腐蚀缺陷相互依赖生长的物理过程。此外，管道失效数据是管道结构退化到临界值的直接体现，蕴含了宝贵的管道完整性信息。为了准确地反映腐蚀管道的安全水平，腐蚀管道结构可靠性评价中涉及的参数不确定性、随机变量之间的相关性以及失效数据均需要加以考虑。然而，在现有的腐蚀天然气管道结构可靠性评价中，鲜有研究全面考虑随机变量之间相关性的影响，更没有涉及到管道失效数据对腐蚀管道结构可靠性评价结果的更新和校正。基于此，本文建立了考虑失效数据和随机变量之间相关性的腐蚀管道可靠性评价方法，以完善目前的研究，为提高腐蚀管道的安全管理提供理论基础。

1 腐蚀管道结构可靠性预测

腐蚀管道结构的可靠性评价是一个典型的预测问题，其利用管道在线检测得到的有限数据，评估未来一段时期内管道结构的可靠性，并预测管道系统达到极限状态的时间，从而制定相应的预防性维修策略。

1.1 管道极限状态方程和管道腐蚀缺陷生长模型

管道腐蚀缺陷存在两种极限状态：小孔泄漏失效和爆裂失效。对于一个给定的管道腐蚀缺陷，给出管道在时间t时对应小孔泄漏失效和爆裂失效的极限状态方程g1(t)和g2(t)分别如下[17-18]：

g1(t)=0.8wt-dmax(t)

(1)

g2(t)=pb(t)-pop(t)

(2)

(3)

式中:0.8为安全系数；wt为管道壁厚(mm)；t为上一次在线检测后经过的时间(a)；dmax(t)为时间t时管道腐蚀缺陷的最大深度(mm)；pop为管道运行压力(MPa)；pb(t)为腐蚀缺陷处的管道爆破压力(MPa)；χ为模型误差；σu为抗拉强度(MPa)；D为管道直径(mm)；l(t)为时间t时管道腐蚀缺陷的轴向长度(mm)。

g1(t)≤0和g2(t)≤0分别代表含腐蚀缺陷管道小孔泄漏失效和爆裂失效的发生。含腐蚀缺陷管道小孔泄漏失效和爆裂失效对应的数学表达式如下[19]：

Psl(t)=Prob[(g1(t)≤0)∩(g2(t)>0)]

(4)

Pbu(t)=Prob[(g1(t)>0)∩(g2(t)≤0)]

(5)

式中：Psl和Pbu分别为含腐蚀缺陷管道的小孔泄漏失效概率和爆裂失效概率。

在给定的管道腐蚀缺陷处发生小孔泄漏和爆裂失效被认为是互斥事件[20]，因此含腐蚀缺陷管道的总失效概率Pf为发生小孔泄漏和爆裂失效的概率之和：

Pf(t)=Psl(t)+Pbu(t)

(6)

腐蚀缺陷深度是影响腐蚀管道结构可靠性评估的一个关键参数，而腐蚀缺陷长度的增长对腐蚀管道结构可靠性评价结果的影响很小[20]，故假设管道腐蚀缺陷长度不随时间增长。本文采用线性随机变量模型来描述管道腐蚀缺陷深度的生长，将多个腐蚀缺陷的年深度增量量化为具有相关性且服从特定分布的多维随机变量：

di,max(t)=di,max(0)+Xi(t)

(7)

其中：

(8)

式中：di,max(t)为管道腐蚀缺陷i在时间t时的最大深度(mm)；di,max(0)为管道腐蚀缺陷i的初始最大深度(mm)，通过内检测数据来确定；Xi(t)为管道腐蚀缺陷i的总深度增量(mm)；ΔXi,j(Δt)表示管道腐蚀缺陷i在第j年的年深度增量，即深度腐蚀速率(mm/a)；Δt为模拟时间步长，取1 a；T为腐蚀管道结构可靠性的评价周期(a)。

1.2 基于Copula函数的随机变量之间相关性描述

腐蚀管道结构可靠性评价涉及的随机变量之间的相关性可分为两个层次：第一层为管道结构参数、缺陷尺寸参数等随机变量之间的相关性；第二层为多个腐蚀缺陷生长过程的相关性。前者是一个二维随机变量之间的相关性问题，而后者则是与腐蚀缺陷数量有关的多维随机变量之间的相关性问题。具体来说，本文考虑了管径与壁厚、腐蚀缺陷初始长度与初始深度以及多个腐蚀缺陷年深度增量之间的相关性，它们都可以采用具有特定相关系数矩阵的Copula函数来描述和解决。

Copula函数是一个包含n(n≥2)个标准均匀分布变量Ui(i=1,2,…,n)的联合分布函数[21]。本文采用高斯Copula函数来描述本研究所涉及的随机变量之间的相关性：

C(u1,u2,…,un)=Φn(Φ-1(u1),Φ-1(u2),…,Φ-1(un);R)

(9)

式中：C(u1,u2,…,un)表示Copula函数，其中ui是Ui的值(i=1,2,…,n);Φn(·;R)表示具有相关系数矩阵R(n×n)的n维标准正态分布函数，其中Φ-1(·)是一维标准正态分布函数的逆函数;R的非对角元素rij(i,j=1,2,…,n；i≠j)代表Φ-1(ui)与Φ-1(uj)之间的线性相关系数。

利用高斯Copula函数可以非常便捷地生成具有特定相关系数的n(n≥2)维随机变量样本，以本研究为例，首先通过具有相关系数矩阵R的高斯Copula函数Φn(·);R)生成相关样本ui(i=1,2,…,n)；然后利用等概率密度边缘变换方法[见公式(10)]，可生成具有特定分布的相关随机变量样本xi(i=1,2,…,n)。

Fi(xi)=ui(i=1,2,…,n)

(10)

式中：Fi(·)表示累积分布函数。

1.3 腐蚀管道失效概率计算

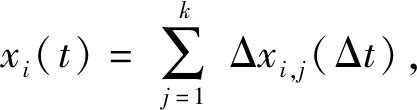
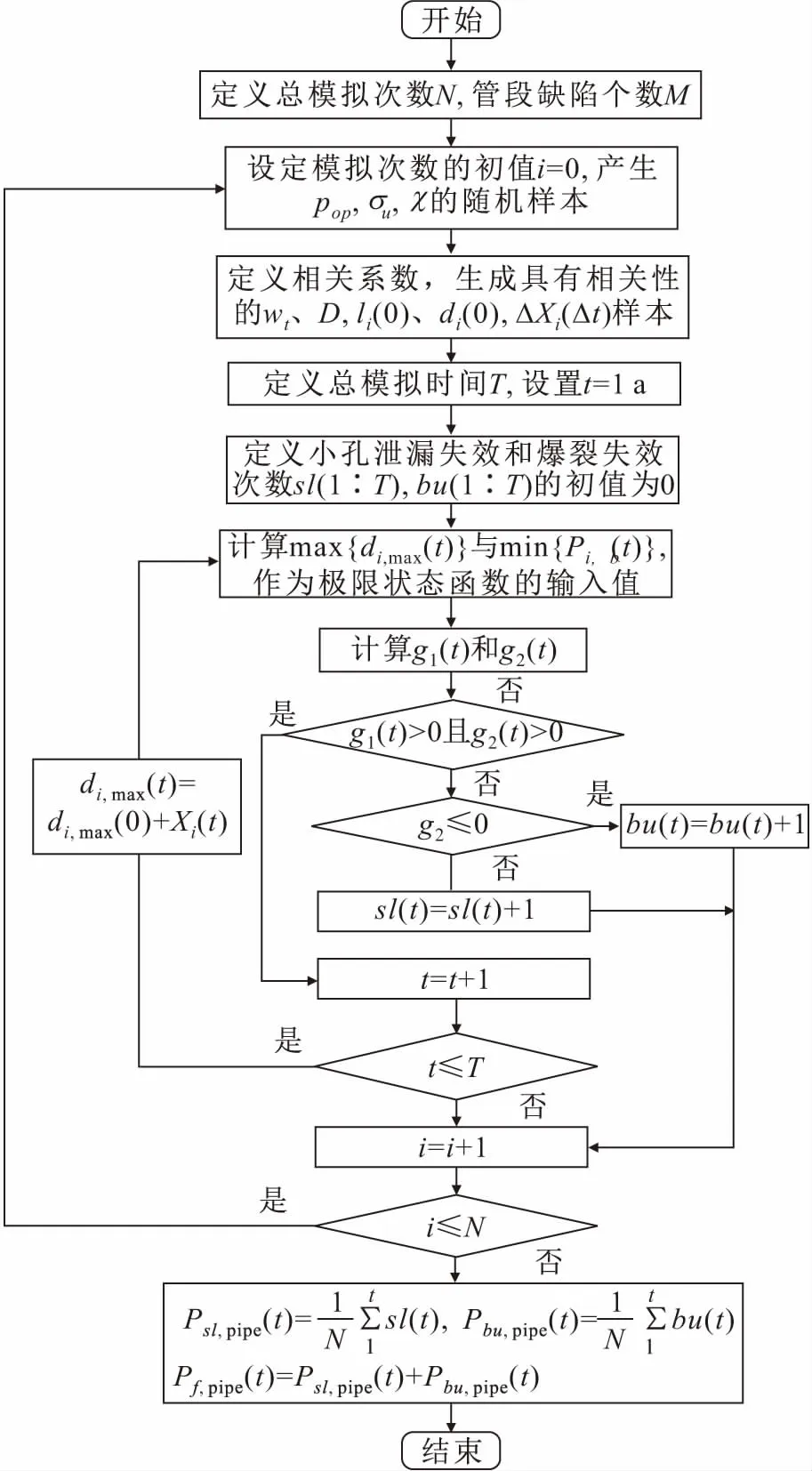
图1 含n个腐蚀缺陷的管段失效概率模拟计算流程图Fig.1 Flow chart for simulating calculation of failure probability of the pipeline segment with n corrosion defects注：pi,b(t)为腐蚀缺陷i处的管道爆破压力(MPa);Psl,pipe、Pbu,pipe和Pf,pipe分别表示含腐蚀缺陷管道的小孔泄漏失效概率、爆裂失效概率和总失效概率。

2 腐蚀管道结构可靠性评价结果的更新和校正

2.1 腐蚀管道失效概率的最佳分布描述

贝叶斯更新的对象为概率分布的参数值，故先基于秩回归方法确定失效概率的最佳分布，再通过贝叶斯方法更新腐蚀管段失效概率分布函数的参数。本文选取5种候选分布来描述腐蚀管段的失效概率，并从中得到最佳分布。具体步骤如下[1]：

(1) 选择指数分布、正态分布、对数正态分布、威布尔分布和耿贝尔分布作为腐蚀管道失效概率的候选分布，每种候选分布的累积分布函数和处理后的线性方程列于表1。

表1 描述腐蚀管道失效概率候选分布的累积分布函数和线性方程Table 1 Cumulative distribution functions and linear equations of candidate distributions describing the failure probability of corroded pipelines

(2) 将腐蚀管段逐年的失效概率{t,P(t)}代入各累积分布函数的线性方程中，采用秩回归方法获得线性方程系数A和B的值，进一步计算得到各累积分布函数的相应参数值。

(3) 采用下式计算各线性方程的相关系数，相关系数绝对值最大的分布则为描述腐蚀管道失效概率的最佳分布。采用其累积分布函数F(t|θ)表示腐蚀管段的失效概率，其中θ为上述步骤(2)得到的该累积分布函数的相应参数值。线性方程相关系数ρ的计算公式为

(11)

2.2 腐蚀管道失效概率分布函数的参数更新

在贝叶斯方法中，失效概率分布函数的参数θ被视为随机变量，并具有先验分布函数p(θ)。更新后的参数θ的分布称为后验分布，其概率密度函数可根据Bayes定理[23]计算如下：

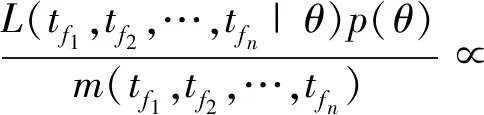
L(tf1,tf2,…,tfn|θ)p(θ)

(12)

其中：

(13)

(14)

式中：∝表示正比关系；tfi(i=1,2,…,n)为管道失效数据，即管道由于腐蚀缺陷而失效的时间；L(tf1,tf2,…,tfi|θ)为管道失效数据的抽样密度函数；m(tf1,tf2,…,tfi)为管道失效数据的边缘密度函数，其不依赖于参数θ；p(θ|tf1,tf2,…,tfi)为参数θ的后验分布函数。

为了便于描述，将参数θ设为q维实向量，同时为了得到每个未知参数θi的概率特性，推导得出θi的边缘密度函数如下：

p(θi|tf1,tf2,…,tfi)

(15)

式中：θ(-i)表示在θ中除去参数θi的剩余参数向量。

马尔科夫蒙特卡洛模拟技术是一种解决上述复杂高维函数积分问题的有效方法。该方法通过迭代得到参数向量θ的一个仿真序列θ(j)(j=1,2,…,),如果j足够大，θ(j)将收敛于一个由后验分布中生成的随机序列。因此，执行大量迭代后，算法产生的仿真序列θ(m),θ(m+1),…,θ(m+k),可认为是来自后验分布的样本；相反，θ(1)，θ(2)，…，θ(m-1)被认为是算法的老炼期，不能作为代表后验分布的样本。图2展示了马尔科夫蒙特卡洛模拟技术的原理。

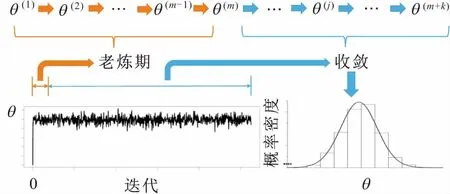
图2 马尔科夫蒙特卡洛模拟技术的原理图Fig.2 Principle diagram of Markov Monte Carlo simulation technology

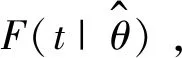
本次研究涉及的模型和方法较多，本研究整体方法流程图以及各个模型和方法在不同阶段的应用，见图3。

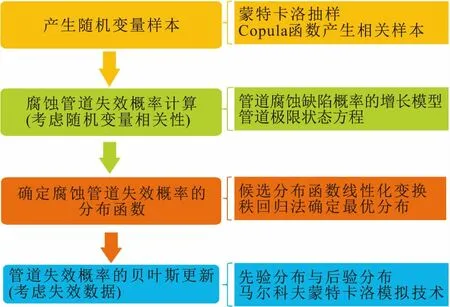
图3 本研究整体方法流程图Fig.3 Overall method flow chart of this article

3 算例分析

3.1 案例描述

本文采用我国某天然气管道的腐蚀失效数据，应用上述方法对一长2 km且包含5个腐蚀缺陷的管段进行了可靠性预测与更新，以验证本文方法的可靠性和可行性。根据2006年的在线检测报告结果，得到该管道和腐蚀缺陷基本参数的概率特征，见表2。腐蚀管道结构可靠性评价中所涉及的随机变量之间相关性的相关系数取值，见表3。该管道于2016年(上一次在线检测后的第10年)发生一起腐蚀失效事件，标记时间tf1=10(指上一次在线检测的时间是2006年，对应的标记时间为第0年)。

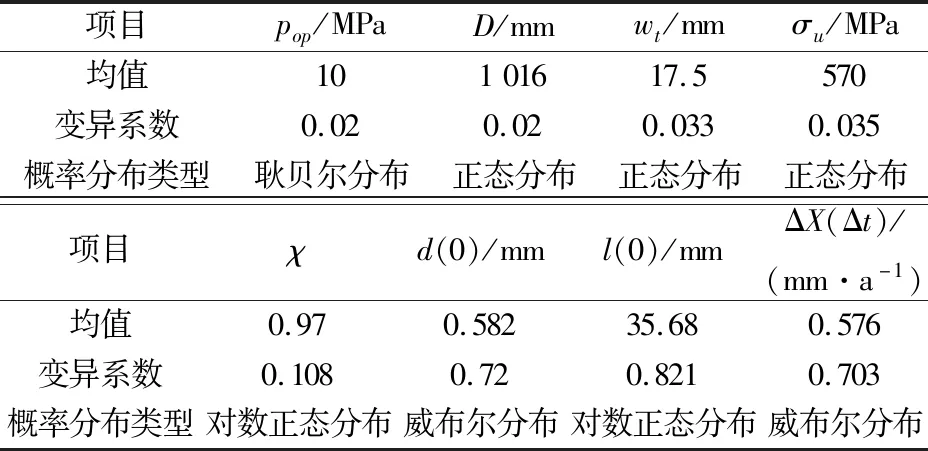
表2 管道和腐蚀缺陷基本参数的概率特征Table 2 Probability characteristics of basic parameters of the pipeline and the corrosion defects

表3 随机变量之间相关性的相关系数取值Table 3 Values of correlation coefficients between random variables

3.2 随机变量之间的相关性对腐蚀管道结构可靠性评价的影响

图4、图5和图6展示了基于Copula函数生成的随机变量相关样本，结果表明产生的随机变量相关样本确实具有特定的相关性，从而验证了Copula函数生成相关样本的有效性。

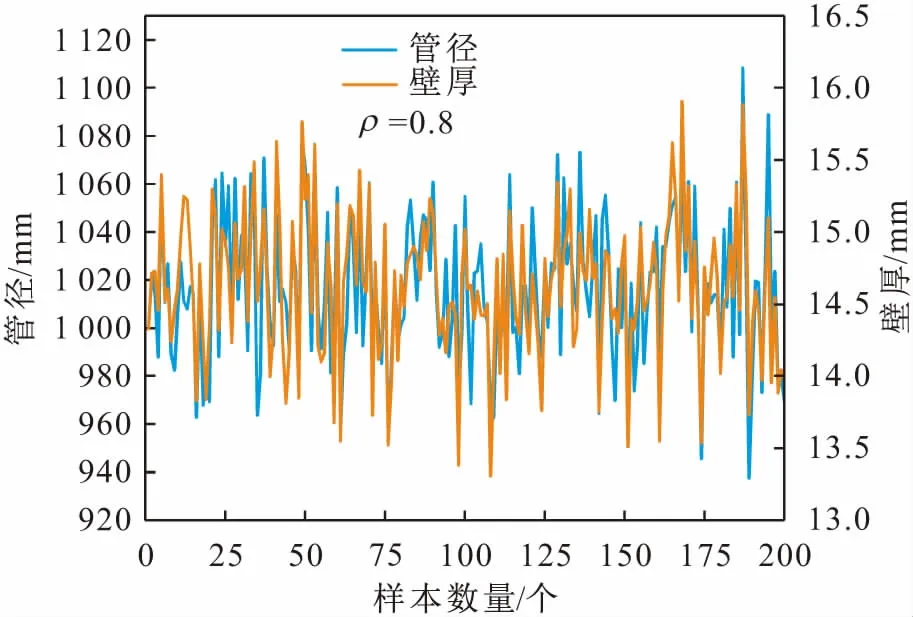
图4 管径与壁厚的相关样本Fig.4 Correlated samples of diameters and wall thickness

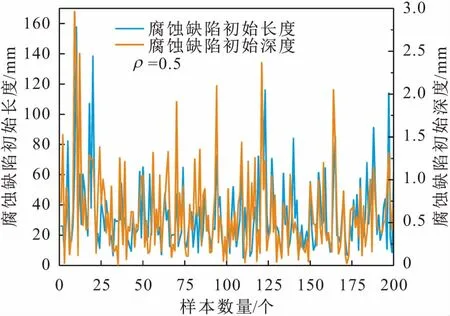
图5 腐蚀缺陷初始长度与初始深度的相关样本Fig.5 Correlated samples of defect initial lengths and initial depths

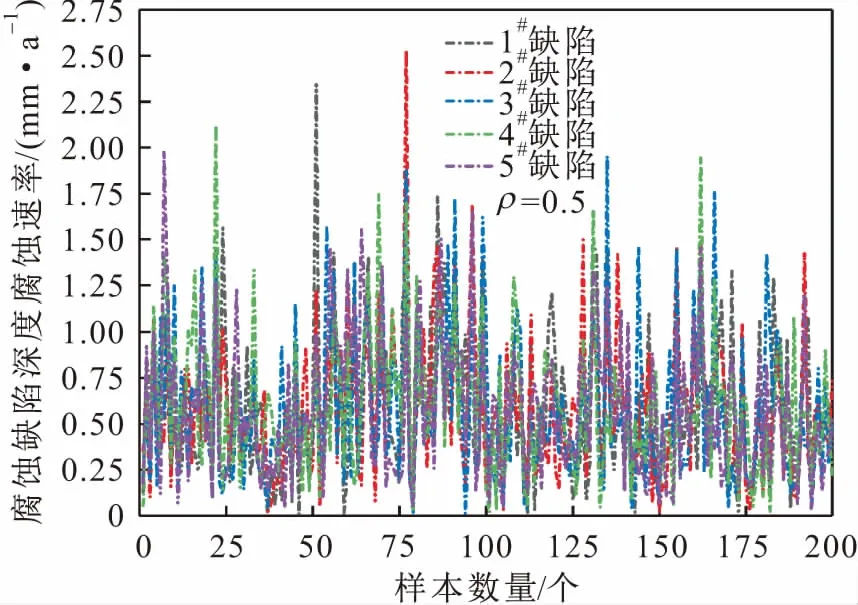
图6 不同腐蚀缺陷深度腐蚀速率之间的相关样本Fig.6 Correlated samples of defects depth growth rate

通过100万次的蒙特卡洛模拟试验，在50 a预测周期内分别对考虑随机变量之间相关性和不考虑随机变量之间相关性的腐蚀管段发生的小孔泄漏失效概率、爆裂失效概率和总失效概率进行了计算，其计算结果见图7。

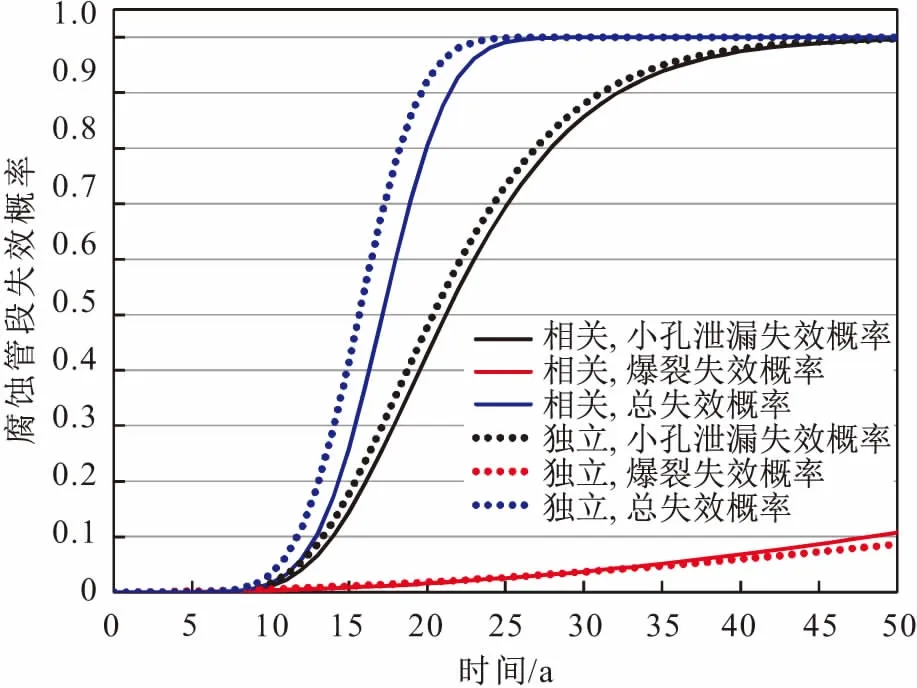
图7 随机变量之间的相关性对腐蚀管道失效概率的影响Fig.7 Effect of correlations between random variables on pipeline failure probability

由图7可见，考虑随机变量之间的相关性会引起腐蚀管段小孔泄漏失效概率和总失效概率的降低，而对腐蚀管段爆裂失效概率的影响则显现出双向性，即在大约27 a之前，会引起腐蚀管段爆裂失效概率的降低，在27 a之后又会引起腐蚀管段爆裂失效概率的增加。这种现象的出现与失效模式对应的管道极限状态方程和实际管道失效数据有关，这是由于工程实际中，与管道结构可靠性评价有关的一些参数之间确实存在相关性，所以考虑参数相关性的腐蚀管道失效概率的预测结果更为准确。模拟参数相关性的关键在于相关系数的确定，但目前尚未有明确的数关系数取值方法，通常根据管道内检测数据进行统计或经验判定。

3.3 失效数据对腐蚀管道结构可靠性的更新和校正

利用管道腐蚀失效数据对腐蚀管道结构可靠性进行更新的前提是将管道失效概率拟合为具有一定参数的概率分布。为了选择最优的概率分布函数来描述腐蚀管段的总失效概率，本文采用秩回归方法计算出了描述管道失效概率的5种候选分布函数的相关系数，见表4。

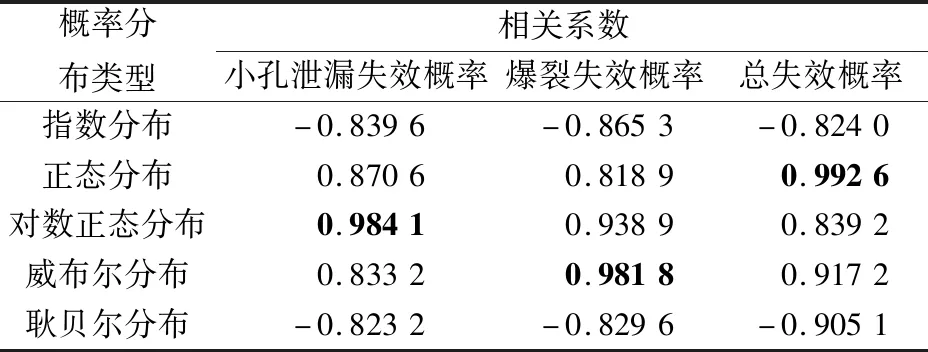
表4 描述管道失效概率的5种候选分布函数的相关系数计算结果Table 4 Calculation results of correlation coefficients of the five candidate distribution functions describing pipeline failure probability

由表4可以得到描述腐蚀管道失效概率的最佳分布及其分布函数。由于后文的主要研究目标为通过失效数据来更新和校正腐蚀管道结构的可靠性评价结果，而不关注管道具体的失效模式，故本文基于腐蚀管道总失效概率来说明贝叶斯推断在本研究中的具体应用。表4显示正态分布是描述腐蚀管段总失效概率的最佳分布，故采用表1中的线性方程计算得到了相应的分布函数的参数值为μ=17.003 3、σ=3.285 8，则腐蚀管段的总失效概率分布函数F(t|θ)的表达式为

(16)

采用贝叶斯方法，通过引入失效数据对公式(16)所描述的正态分布函数中的均值μ和标准差σ参数进行更新。由于μ和σ都具有正的增量，故采用伽马分布作为它们的先验分布。μ和σ在失效分布函数F(t|θ)中的先验信息可以用来定义它们的先验分布函数，采取均值和均值的10%分别作为它们的先验分布的均值和标准差。因此，p(μ)和p(σ)分别可表示如下：

(μ>0,α1>0,λ1>0)

(17)

(σ>0,α2>0,λ2>0)

(18)

式中：α1=170.033；λ1=10；α2=32.858；λ2=10；Γ(·)表示伽马函数。

根据管道腐蚀失效数据(失效时间为2016年，标记时间tf1=10)，结合贝叶斯定理，参数μ和σ的后验密度函数可表示为

p(μ,σ|tf1)∝fsl(tf1|μ,σ)×

(19)

式中:fsl(tf1|μ,σ)是关于参数μ和σ的似然函数；sl表示小孔泄漏事件。

采用OpenBUGS软件对本算例进行贝叶斯更新的模型示意图，见图8。由于这是一个多参数模型，因此为每个参数设置了两条马尔科夫链，每条链迭代50万次产生后验样本，认为前5 000次迭代为老炼期。表5列出了参数μ和σ的后验均值和95%置信区间。

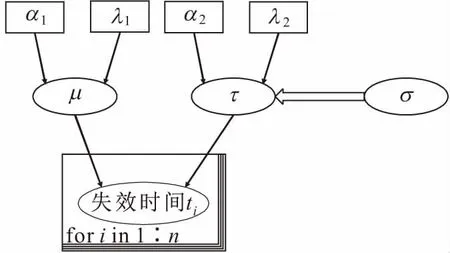
图8 基于OpenBUGS的贝叶斯更新模型示意图Fig.8 Diagram of OpenBUGS Bayesian updating model

表5 参数μ和σ的后验均值和95%置信区间Table 5 Posterior mean and 95% confidence interval of parameters μ and σ

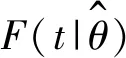
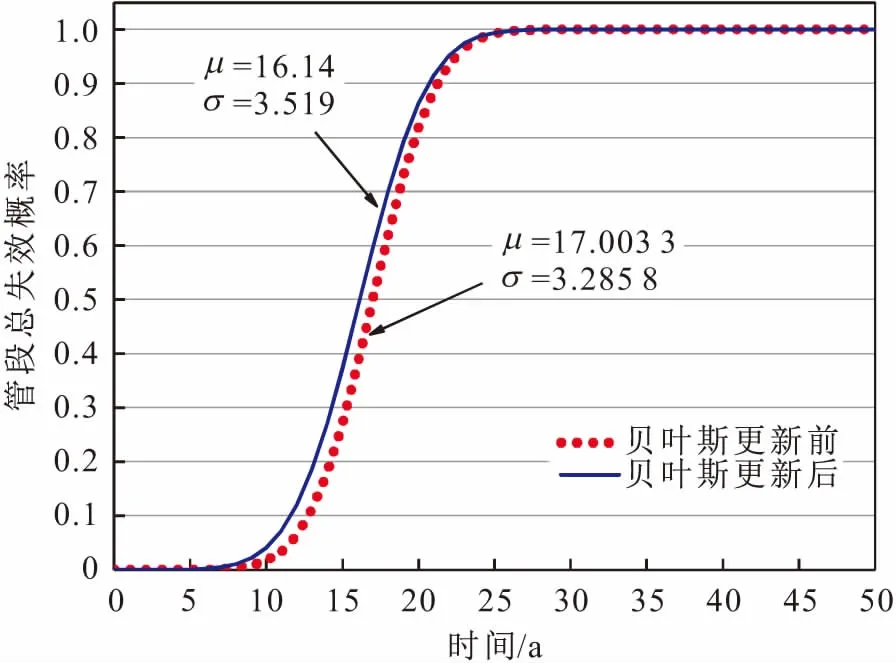
图9 失效数据对管道失效概率的更新和校正Fig.9 Update and correction of failure probability of pipeline with the failure data

由图9可见，贝叶斯更新前，管道失效时间的均值点估计为17.003 3 a，管道于第10年发生了一起小孔泄漏失效，由此可知管道的腐蚀情况比预期严重；基于失效数据，采用贝叶斯方法更新当前的管道失效概率评估结果，结果表明同一时间更新后的管段失效概率比更新前更高，更新后的管道失效时间均值点估计为16.14 a，这与前述分析相一致,即管道腐蚀情况比预期严重。可见，更新后的管道失效概率引入了失效数据蕴含的有效信息，能更准确地反映管道的腐蚀状态。需要说明的是，失效数据使后验均值低于先验均值，但后验均值不可能等于10 a，因为贝叶斯更新的意义是在先验分布的基础上，引入最新数据，得到后验分布，先验信息仍然是主导后验分布的主要原因。就本研究而言，管道是一个包含多个腐蚀缺陷的系统，先验分布是对管道系统整体的认知，失效数据则是关于管道上某个腐蚀缺陷的信息，因此失效数据可对管道结构可靠性评估结果起到更新和校正的作用。