综合能源系统中热力子系统的稳态特性分析

屈鲁，欧阳斌，袁志昌，张树卿，曾嵘

综合能源系统中热力子系统的稳态特性分析

屈鲁，欧阳斌，袁志昌，张树卿，曾嵘

（电力系统及发电设备控制和仿真国家重点实验室(清华大学电机工程与应用电子技术系)，北京市 海淀区 100084）

综合能源系统(integrated energy system，IES)涵盖能源形式多样，涉及运行模式复杂，包含控制设备和耦合环节丰富，给其稳态建模和稳态潮流计算带来了挑战。为了获取综合能源系统中热力子系统的稳态特性，给出了典型综合能源系统的拓扑架构；分别建立了电力子系统、热力子系统、冷力子系统和分布式能源站的稳态模型，进而建立了混合潮流模型，并利用Newton-Raphson算法进行了混合潮流求解；分析了热力子系统的关键技术参数(包括源节点的供水温度、负荷节点的出水温度、热网管道的长度和直径、热负荷功率) 变化对综合能源系统稳态潮流的影响。分析结果可支撑综合能源系统的规划、设计及优化运行。

综合能源系统(IES)；热力子系统；稳态建模；稳态潮流

0 引言

综合能源系统(integrated energy system，IES)是能源互联网物理层的基本组成部分，可以实现不同类型能源的互补和高效利用。从源侧来看，综合能源系统包含冷、热、电、气等不同形式能源；从网侧来看，综合能源系统包含冷网、热网、电网、气网等不同能源网络架构；从储侧来看，综合能源系统不仅含有储电，还包含储热、蓄冷等；从荷侧来看，综合能源系统除了主要的电力负荷之外，还涵盖热负荷和冷负荷。综合能源系统在源、网、荷、储侧的多元化，决定其模型将极其复杂[1-8]。

综合能源系统建模技术是研究其潮流状态和优化其规划运行的基础[9]。文献[10]建立了综合能源系统中电力和天然气子系统的数学模型，对电力系统潮流计算进行推广，提出了一种电‒气多能流整体计算方法。文献[11]考虑了负荷和可再生能源发电的时空相关性，基于Nataf变换和点估计法提出了一种电‒气耦合综合能源系统的概率多能流计算方法。文献[12]建立了综合能源系统的生产、传输和消费环节的数学模型，采用Energy Hub联系各环节，得到了综合能源系统的整体数学模型。文献[13]基于热电联产的电、热输出之间的关系对Energy Hub的不同运行模式进行了分析，在此基础上提出了一种多能流的分解计算方法，但是文中仅考虑了热负荷，没有考虑热网模型。文献[14]建立了综合能源系统中电、热、气3个子系统的数学模型，选取合适的优化变量建立了多时段最优多能流模型，采用智能优化算法对模型进行了求解。虽然国内外对综合能源系统的稳态建模已开展初步研究，但是在模型的精确性、求解速度、工程实用性等方面仍有待提升。

为了获取综合能源系统中热力子系统的稳态特性，本文首先给出典型综合能源系统的拓扑架构，然后建立综合能源系统稳态模型，最后分析热力子系统的关键技术参数变化对综合能源系统稳态潮流的影响。

1 综合能源系统拓扑架构

为分析综合能源系统中热力子系统的稳态特性，本文采用图1所示的综合能源系统拓扑，该系统采用33节点三相平衡电力系统[15]与修改的9节点热力系统[16]耦合，为减少能量传输损失，冷力子系统直接与负荷连接。

其中，冷热电耦合环节采用基于燃气内燃机的分布式能源站，图2为其拓扑结构和能流关系。图2中：g为输入合成气的能量；GE,E、GE,H和GE,G分别为燃气内燃机输出电功率、热功率和烟气的转换效率；HE和HE,W分别为热水换热器及缸套水热水换热器的转换效率；HP和AHP分别为热泵及吸收式热泵的转换效率；CP,C和CP,E分别为功冷并供设备输出电功率和冷功率的转换效率；LHS为低温热源的转换效率；和1−分别为从热泵输出的热量进入储热罐和进入吸收式热泵及热水换热器的分配系数；和1−分别为储热罐输出热量进入吸收式热泵和功冷并供设备的分配系数；和1−分别为从热泵输出的热量进入低温热源和热水换热器的分配系数；e、h、c分别为电力子系统、热力子系统和冷力子系统输出的能量。

图1 一种典型的综合能源系统拓扑

图2 分布式能源站拓扑

2 综合能源系统稳态建模

综合能源系统稳态建模是对综合能源系统进行稳态特性分析的基础，其主要包括电力子系统、热力子系统、冷力子系统和分布式能源站稳态建模4部分。

2.1 电力子系统稳态建模

电力子系统稳态模型可采用传统配电系统模型。若配电网有e个节点，节点1为平衡节点，节点2到节点1+pv为PV节点，其余为PQ节点。反映节点功率与节点电压、相角之间关系的节点功率方程[15]为：

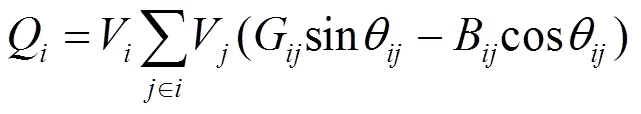
式中：V和V分别为节点和(,=1,2,…,e)的电压；P和Q分别为节点的注入有功功率和无功功率；gen,i和gen,i分别为节点上发电机发出的有功功率和无功功率；load,i和load,i分别为节点上负荷的有功功率和无功功率；G和B分别为节点和之间导纳Y的实部和虚部；θ为节点和之间的相角差。

2.2 热力子系统稳态建模

热力子系统通过供水管道和回水管道连接热源与用户，供热管道水头损失、质量流率以及每个供热节点的供水温度、回水温度往往是热力系统能量流求解的关键变量，其求解模型可分为水力模型和热力模型2部分。

2.2.1 水力模型

基于图论思想对热力子系统的管道特性进行描述，借鉴电力系统基尔霍夫定律，对热力管网中水流的流动规律进行建模，其能量流连续性方程[15-16]可描述为

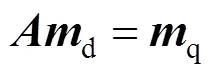
式中：为热力子系统的节点‒管道关联矩阵；d为管道的水流质量流率；q为节点的注入水流质量流率。

水头损失是由于管道摩擦而引起的单位长度的压力变化。在一个闭合回路内，水头损失的和为0，即

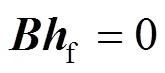
式中：为热力系统的回路‒管道关联矩阵；f为水头损失。

2.2.2 热力模型

热力模型的求解部分主要涉及以下3种温度：供水温度s(从热网进入各热负荷节点时的温度)、出水温度o(各热负荷节点出水温度，为已知量)以及回水温度r(多个节点的出水混合到回水管道时的温度)。

各节点热功率[15-16]可表示为

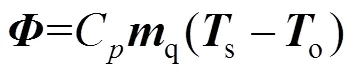
式中C为水的比热。

考虑到管道热损失，在其传输中管道首末节点的水流温度的降落为

式中：start和end分别为水流进入和离开管道时的温度，℃；a为外界环境温度，℃；为管道单位长度的热传导系数，W/(m·K)；为管道长度，m。

在多个管道的交汇节点，其汇合后的温度计算式为

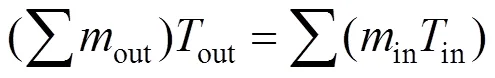
式中：in、out分别为进、出水管道温度，℃；in、ou分别为进、出水管道质量流率，kg/s。

2.3 冷力子系统稳态建模

冷力子系统与热力子系统的模型类似，亦可以由式(5)—(9)描述，此处不再赘述。

2.4 分布式能源站稳态建模

分布式能源站采用能源集线器理论[17]进行建模，得到能源站的数学模型为

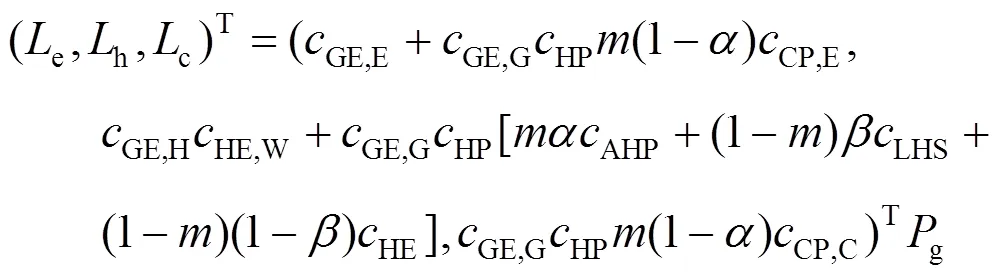
在以热定电/冷的运行模式下，得到能源站的热电比和热冷比分别为

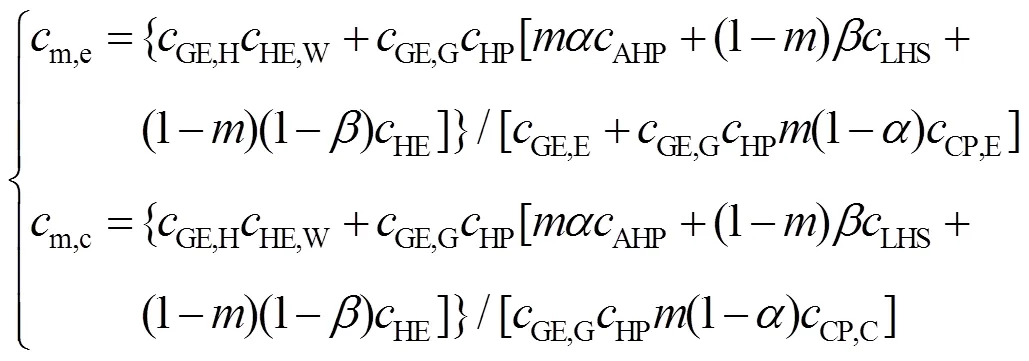
能源站各能量转换元件的转换效率及能量流的分配系数取值如表1所示。

表1 能源站的耦合系数

经计算，得到能源站的热电比m,e为0.54，热冷比m,c为3.87。

2.5 混合潮流模型

对综合能源系统各子系统进行解耦建模是对系统进行稳态潮流分析的基础。基于电力子系统、热力子系统、冷力子系统和分布式能源站的模型，建立综合能源系统的混合潮流模型[18]：

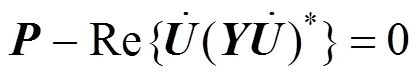
式(12)、(13)分别表示电力子系统的有功偏差和无功偏差；式(14)—(17)分别表示热力子系统的节点热功率偏差、供热网络回路压力降偏差、供热温度偏差和回热温度偏差；、和分别为系统给定有功功率、无功功率和热功率；和分别为电力子系统节点电压向量和导纳矩阵；s为供热网络形成的降阶的关联矩阵；为管道的阻抗系数；s、r分别为与供热网络、回热网络的结构和流量有关的矩阵；s、r分别为与供热温度、输出温度有关的列向量。

对于综合能源系统，潮流计算的本质是在给定一系列条件下求取系统运行点的过程，可通过Newton-Raphson算法求解式(12)。其中，电力子系统、热力子系统负荷分别如表2、3所示。

3 综合能源系统特性分析

对于热力子系统，从“源”和“荷”2个角度来开展关键技术参数对综合能源系统稳态潮流的影响特性分析。首先是从“源”的角度，即热力子系统管网内部的相关参数，具体包括热源节点的供水温度、负荷节点的出水温度、热网管道的长度和直径；其次是从“荷”的角度，即热力子系统所供应的热负荷的功率。

3.1 源节点供水温度

在其他技术参数均一致的情况下，设置100、90、80、70℃共4组不同的源节点供水温度，计算不同源节点供水温度下的稳态潮流，得到管道稳态流量、节点供水温度和节点回水温度，见图3。

表2 电力子系统负荷

表3 热力子系统负荷

由图3(a)可知，源节点供水温度越低，管道内稳态流量越大；由式(7)的热功率方程也可得到同样的结论。由图3(b)可知，当源节点供水温度降低时，各节点供水温度也随之降低，但各节点供水温度之间的相对关系不变，即各节点供水温度的变化趋势不变。由图3(c)可知，在不同的源节点供水温度下，各负荷节点的回水温度仍与设置的出水温度相同，为50℃，非负荷节点的回水温度随源节点供水温度的下降而略微上升，变化幅度很小。

图3 不同源节点供水温度下的稳态特性

同时，计算结果表明：在计算耦合环节输出热功率时，热力子系统多个变量的变化相互抵消，使得耦合环节的热能出力基本保持不变。在“以热定电”的运行模式下，耦合环节的电能出力也基本不变。同理，在“以热定冷”的运行模式下，冷力子系统供给的功率也基本不变。

3.2 负荷节点出水温度

在其他技术参数均一致的情况下，设置50、40、30、20℃共4组不同的负荷节点出水温度，计算不同负荷节点出水温度下的稳态潮流，得到管道稳态流量、节点供水温度和节点回水温度，如图4所示。

由图4(a)可知，负荷节点出水温度越低，管道内稳态流量越小；由式(7)的热功率方程也可得到同样结论。由图4(b)可知，负荷节点出水温度降低，各节点供水温度也相应降低，其降低幅度远小于出水温度的降低幅度。由图4(c)可知，当负荷节点出水温度降低时，各节点回水温度也随之降低，但各节点回水温度之间的相对关系不变，即各节点回水温度的变化趋势不变。

图4 不同负荷节点出水温度下的稳态特性

3.3 热网管道长度

在其他技术参数均一致的情况下，设置0.5、0.75、1、1.25倍标准长度共4组不同的热网管道长度，计算不同热网管道长度下的稳态潮流，得到管道稳态流量、节点供水温度和节点回水温度，如图5所示。

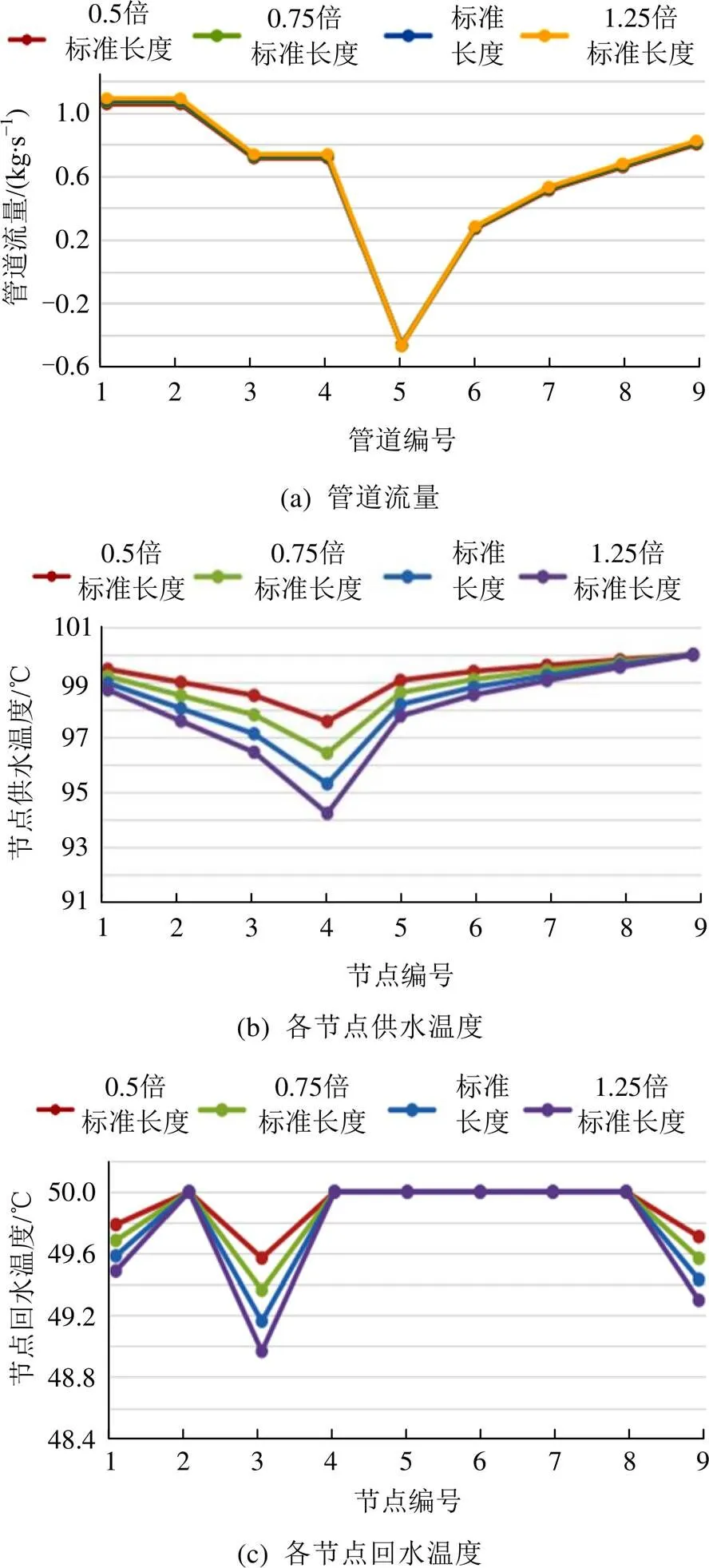
图5 不同管道长度下的稳态特性

由图5可知，当热网管道长度增加时，管道稳态流量有小幅度的增长，各节点供水温度和回水温度有小幅度的下降。这是因为随着热网管道长度增加，热量在以水为介质的传输过程中的损耗增大，表现为温度的损耗增加。如式(8)所示，管道越长，管道末端温度越低，故各节点供水温度和回水温度均下降，且供水温度下降更明显。因此，热力管网供给热功率的温差变小，则管道流量相应增加，从而保证热负荷的充足供给。

3.4 热网管道直径

在其他技术参数均一致的情况下，设置0.5、0.75、1、1.25倍标准直径共4组不同的热网管道直径，计算不同热网管道直径下的稳态潮流，得到管道稳态流量、节点供水温度和节点回水温度，如图6所示。

图6 不同管道直径下的稳态特性

由图6可知，改变热网管道直径，对管道稳态流量、各节点供水温度和回水温度几乎没有影响。在理论上，无论多细的管道，可供的热功率都是无穷大的，但是管道越细阻力越大，当管道直径小于一定数值时，会造成运行不经济。

3.5 节点热负荷功率

在其他技术参数均一致的情况下，设置0.5、0.75、1、1.25倍标准功率共4组不同的热负荷功率，计算不同热负荷功率下的稳态潮流，得到管道稳态流量、节点供水温度和节点回水温度，如图7所示。

图7 不同热负荷下的稳态特性

由图7(a)可知，热网供给的热负荷功率越大，其管道流量也越大，这也符合热功率方程中热功率与流量成正比的关系。而从图7(b)和图7(c)中可以看到，随着热负荷功率的增加，各节点的供水温度和回水温度都有小幅度的上升。

同时，计算结果表明：当热力子系统节点热负荷增大时，电力子系统母线电压得到一定幅度的提升。因为当热负荷增大时，为了满足供热需求，耦合环节的热出力随之增大，在恒定热电比的约束下，耦合环节的电出力也增大，而耦合环节在电力子系统中相当于一个分布式电源，故电源出力增加，对各节点电压起到了一定的支撑作用。并且，当热力子系统热负荷需求发生变化时，冷力子系统供能水平随着热力子系统热负荷功率的增加而提高，耦合环节恒定热冷比的限定，使得耦合环节的热能出力与冷能出力有明确的比例关系，具有同样的变化趋势。

4 结论

建立了综合能源系统的混合潮流模型，利用Newton-Raphson算法进行混合潮流求解，获取了综合能源系统的稳态特性，并探讨了热力子系统的关键技术参数对综合能源系统稳态潮流的影响特性，得到以下结论：

1）源节点供水温度越低，管道内稳态流量越大，各节点供水温度也越低，但各负荷节点的回水温度仍与设置的出水温度相同，非负荷节点的回水温度随源节点供水温度的下降而略微上升，变化幅度很小。

2）负荷节点出水温度越低，管道内稳态流量越小，各节点供水温度也相应降低，各节点回水温度也随之降低，但各节点回水温度的走势不变。

3）当热网管道长度增加时，管道稳态流量有小幅度的增长，管道末端温度降低，故各节点供水温度和回水温度均下降。

4）改变热网管道直径，对管道稳态流量、各节点供水温度和回水温度几乎没有影响。

5）热力管网供给的热负荷功率越大，其管道流量也越大，各节点的供水温度和回水温度都有小幅度的上升。

研究结果可支撑综合能源系统的规划、设计及优化运行。

[1] 余晓丹，徐宪东，陈硕翼，等．综合能源系统与能源互联网简述[J]．电工技术学报，2016，31(1)：1-13．

[2] Quelhas A，Gil E，McCalley J D，et al．A multiperiod generalized network flow model of the US integrated energy system：part I：model description[J]．IEEE Transactions on Power Systems，2007，22(2)：829-836．

[3] Lund H，Münster E．Integrated energy systems and local energy markets[J]．Energy Policy，2006，34(10)：1152-1160．

[4] 曾鸣，刘英新，周鹏程，等．综合能源系统建模及效益评价体系综述与展望[J]．电网技术，2018，42(6)：1697-1708．

[5] 贾宏杰，王丹，徐宪东，等．区域综合能源系统若干问题研究[J]．电力系统自动化，2015(7)：198-207．

[6] 杨晓巳，陶新磊．综合能源技术路线研究[J]．华电技术，2019，41(11)：22-25．

[7] 叶琪超，楼可炜，张宝，等．多能互补综合能源系统设计及优化[J]．浙江电力，2018，37(7)：5-12．

[8] 郭创新，丁筱．综合能源系统优化运行研究现状及展望[J]．发电技术，2020，41(1)：2-8．

[9] 王伟亮，王丹，贾宏杰，等．能源互联网背景下的典型区域综合能源系统稳态分析研究综述[J]．中国电机工程学报，2016，36(12)：3292-3305．

[10] Martinez-Mares A，Fuerte-Esquivel C R．A unified gas and power flow analysis in natural gas and electricity coupled networks[J]．IEEE Transactions on Power Systems，2012，27(4)：2156-2166．

[11] 孙国强，陈霜，卫志农，等．计及相关性的电-气互联系统概率最优潮流[J]．电力系统自动化，2015，39(21)：11-17．

[12] Krause T，Andersson G，Frohlich K，et al．Multiple-energy carriers：modeling of production，delivery，and consumption[J]．Proceedings of the IEEE，2010，99(1)：15-27．

[13] 徐宪东，贾宏杰，靳小龙，等．区域综合能源系统电/气/热混合潮流算法研究[J]．中国电机工程学报，2015，35(14)：3634-3642．

[14] Shabanpour-Haghighi A，Seifi A R．Simultaneous integrated optimal energy flow of electricity，gas，and heat[J]．Energy Conversion and Management，2015，101：579-591．

[15] 骆柏锋，穆云飞，赵波，等．基于统一潮流模型的电‒气耦合综合能源系统静态灵敏度分析[J]．电力系统自动化，2018(1)：29-35．

[16] Liu X，Wu J，Jenkins N，et al．Combined analysis of electricity and heat networks[J]．Applied Energy，2016，162：1238-1250．

[17] Geidl M，Koeppel G，Favre-Perrod P，et al．Energy hubs for the future[J]．IEEE Power and Energy Magazine，2006，5(1)：24-30．

[18] 王英瑞，曾博，郭经，等．电-热-气综合能源系统多能流计算方法[J]．电网技术，2016，40(10)：2942-2950．

Analysis of Steady-state Characteristics of Thermal Subsystem in Integrated Energy System

QU Lu, OUYANG Bin, YUAN Zhichang, ZHANG Shuqing, ZENG Rong

(State Key Lab of Power Systems (Department of Electrical Engineering, Tsinghua University),Haidian District, Beijing 100084, China)

The integrated energy system (IES) includes various energy forms, complex operation modes, abundant control equipment and coupling links, which brings challenges to its steady-state modeling and steady-state power flow calculation. In order to obtain the steady-state characteristics of the thermal subsystem in the IES, the topological structure of the typical IES was provided; the steady-state models of the power subsystem, the thermal subsystem, the cold subsystem and the distributed energy station were established respectively, and then the hybrid power flow model was established, and the Newton- Raphson algorithm was used to solve the hybrid power flow; the influence of the key technical parameters (including the water supply temperature of the source node, the water outlet temperature of the load node, the length and diameter of the heat network pipe, and the heat load power) on the steady-state power flow of the IES was analyzed. The analysis results can support the planning, design and optimal operation of the IES.

integrated energy system (IES); thermal subsystem; steady-state modelling; steady-state power flow

10.12096/j.2096-4528.pgt.19154

TM 721

2019-10-24。

国家重点研发计划项目(2018YFB0905105)。

Project Supported by National Key Research and Development Program of China (2018YFB0905105).

(责任编辑 尚彩娟)