机器人直线运动位置轨迹精度评估方法研究*
2020-06-28王炳荣
郭 军,王炳荣
(北京工业大学 北京市精密测控技术与仪器工程技术研究中心,北京 100124)
0 引 言
随着我国工业机器人产业的发展,对机器人轨迹控制精度提出了更高的要求[1]。
对工业机器人性能特征的研究测量具有非常重要的价值。这些性能标准由国家和国际工业标准定义,也描述了评估它们的方法。然而,将这些标准和方法直接应用于任何机器人可能导致机器人精确度的错误识别。李志杰等[2]应用严密的数学理论和最小二乘误差理论,推导出了用于评价机器人直线运动轨迹成形精度的空间最小二乘直线的通用求解方法。该方法具有求解精度高、算法简便、通用性较强的优点;蔡广宇等[3]提出了空间直线拟合的方法对机器人直线轨迹进行了拟合,通过分析误差分布情况为机器人的位姿误差补偿及精度优化设计提供了依据;瑞典Selspot公司生产的双摄像机测试系统采用了“替代”求解方法,该方法原理是在对机器人进行多次重复测量时,迭用其任意一次运动轨迹上的两点所确定的空间直线来代替所要求的空间最小二乘直线;陈凯强等[4]提出了一种基于NURBS曲线的插值方法和插补的原理,通过MATLAB仿真对该方法进行了测试,显著降低了插值误差和计算量;JOHNEN B等[5]提出了动态时间扭曲(DTW)作为工业机器人运动分析的方法,提出了DTW算法的一种新变体,它允许内插轨迹点的映射,而不会显著增加计算复杂度。
本文采用激光跟踪仪连续测量模式对工业机器人进行直线位置准确度指标测试[6],对机器人直线运动轨迹精度进行评估。
1 位置轨迹准确度测量方法与原理
国家标准GB/T 12642—2013《工业机器人性能规范及其试验方法》规定,位置轨迹准确度是指指令轨迹上m个位置与n次测量的集群中心点之间的最大偏差[8]。
轨迹准确度如图1所示。
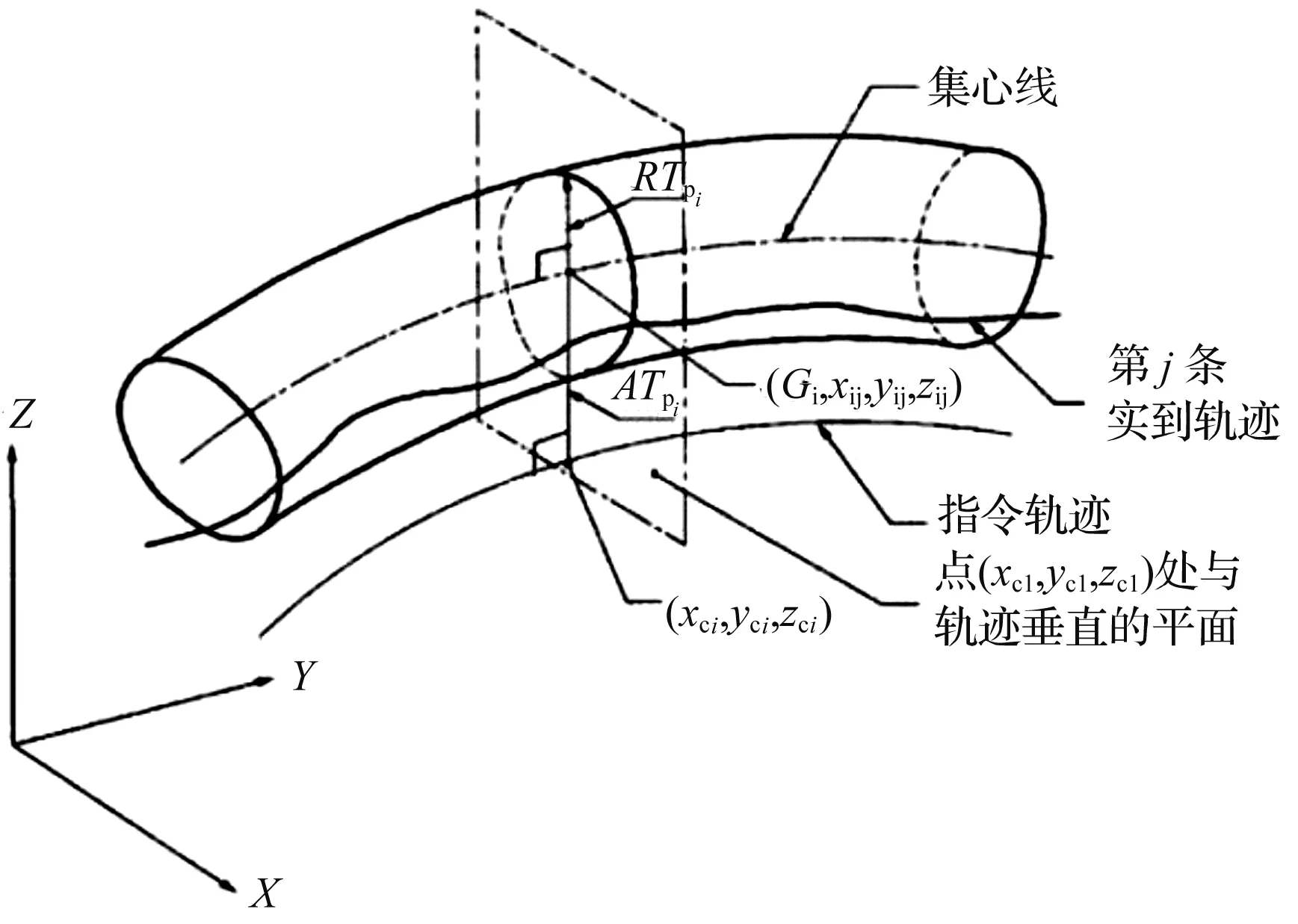
图1 GB/T 12642—2013规定轨迹准确度
位置轨迹准确度的计算方法如下:

(1)
(2)
式中:xci,yci,zci—每个测试点的理论位置坐标;xij,yij,zij—第j条实到轨迹与第i个正交平面交点的坐标。
根据指令轨迹形状与试验速度,笔者沿指令轨迹选择一些计算点及相应的正交平面。
但是标准中没有规定应该构造多少正交平面以及应该放置它们的位置,所以给轨迹的精度评估带来了一定的不确定性。本文采用以下3种方法对直线轨迹位置准确度进行近似计算。
当采样频率较慢、采样点数较少时,采用三次样条插值方法,对测量数据进行处理,可模拟计算出更多实际点的位置,得到更准确的实际轨迹位置:
(1)采用点到直线距离近似计算直线轨迹位置误差。假设机器人在实际执行直线路径任务过程中,起点为P0(x0,y0,z0),终点为P1(x1,y1,z1)每个时刻到达的位置为Pi(xi,yi,zi),可以通过激光跟踪仪测量得到该位置坐标值。
以该位置在理论直线路径上的垂足点P0i(x0i,y0i,z0i)作为机器人实际执行直线路径任务过程中每个时刻的理论位置,则|PiP0i|为该点近似轨迹位置误差,点到直线距离计算轨迹准确度如图2所示。
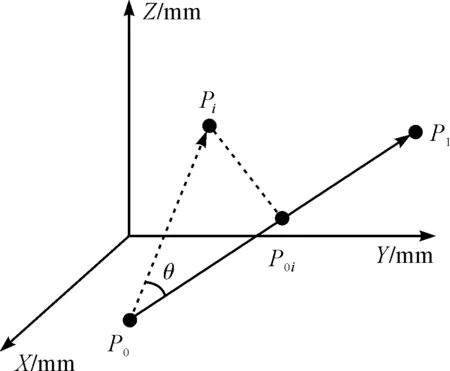
图2 点到直线距离计算轨迹准确度
理论直线方程如下:
(3)
式中:m,n,p—直线的一组方向数。
m=x1-x0
n=y1-y0
p=z1-z0
(4)
转换成参数方程为:
x0i=mti+x0
y0i=nti+y0
z0i=pti+z0
(5)


(6)
每个测量点在理论直线上对应的位置由下式计算:
(7)
则点到直线距离即位置轨迹误差为:

(8)
(2)假设机器人在实际执行直线路径任务过程中,起点为P0(x0,y0,z0),终点为P1(x1,y1,z1),通过激光跟踪仪测量每个时刻到达的位置得到该位置坐标值。
利用三次样条插值方法对测量数据进行计算,将x作为自变量,将y、z看成x的函数,y=y(x),z=z(x),实际轨迹插值点记为Pi(xi,yi,zi),利用分段线性插值方法对理论轨迹直线进行计算。
同样,将x作为自变量,将y、z看成x的函数,理论直线轨迹插值点记为P0i(x0i,y0i,z0i),与实际轨迹插值点数一一对应,近似计算直线轨迹位置误差,如图3所示。
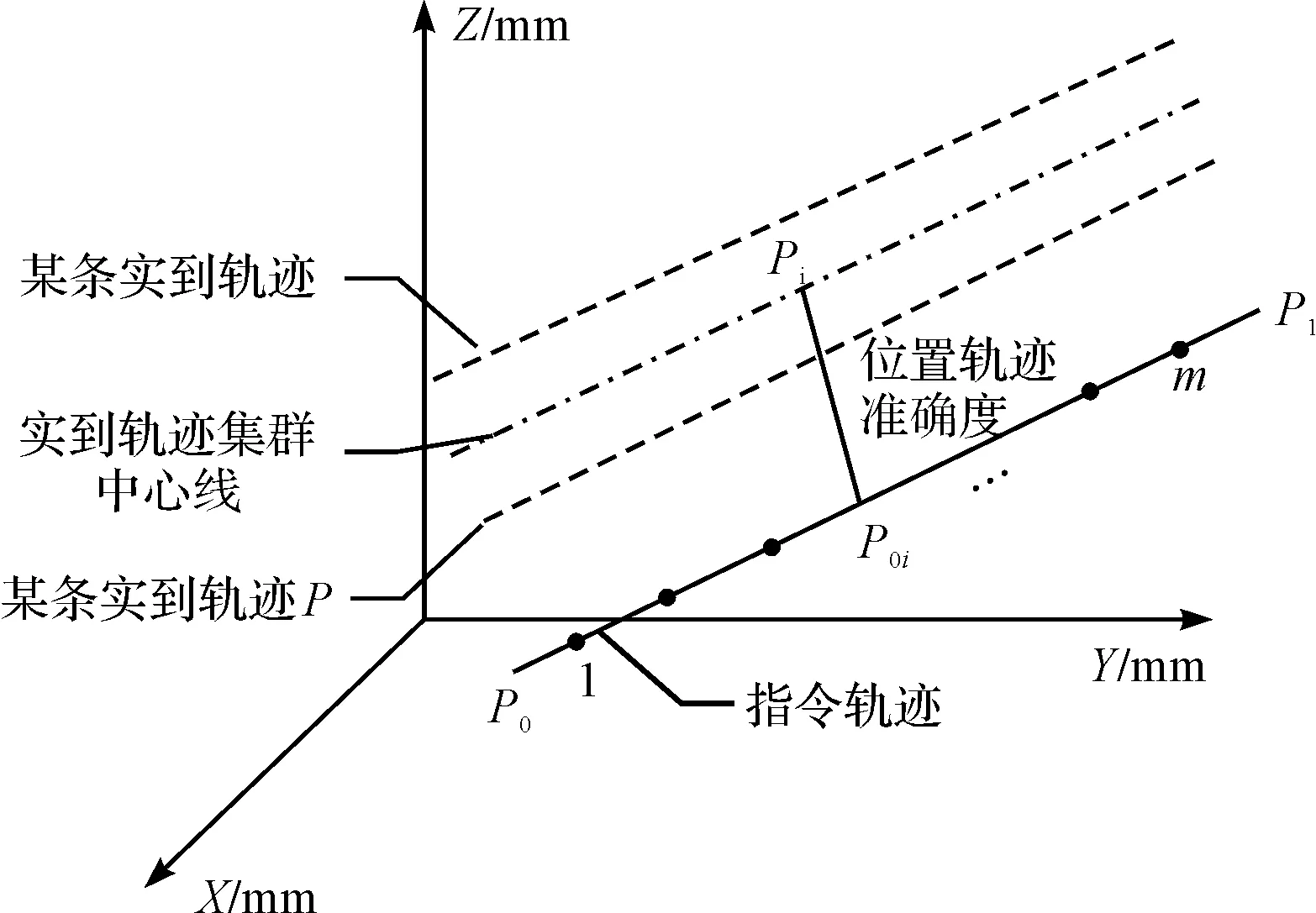
图3 利用插值方法计算轨迹准确度
理论直线方程如下:
(9)
将理论直线进行线性插值,等间距分成m段,则每两点之间的差值如下:
(10)
则插值计算后理论直线上的点如下:
P0i=P0(x0,y0,z0)+(dx,dy,dz)i=
(x0+dxi,y0+dyi,z0+dzi)
(11)
轨迹位置误差为:

(12)
(3)利用速度时间关系求解每个时刻对应理论位置点。假设机器人在实际执行直线路径任务过程中,起点为P0(x0,y0,z0),终点为P1(x1,y1,z1)每个时刻到达的位置为Pi(xi,yi,zi),可以通过激光跟踪仪测量得到该位置坐标值。
利用速度时间关系计算轨迹准确度如图4所示。
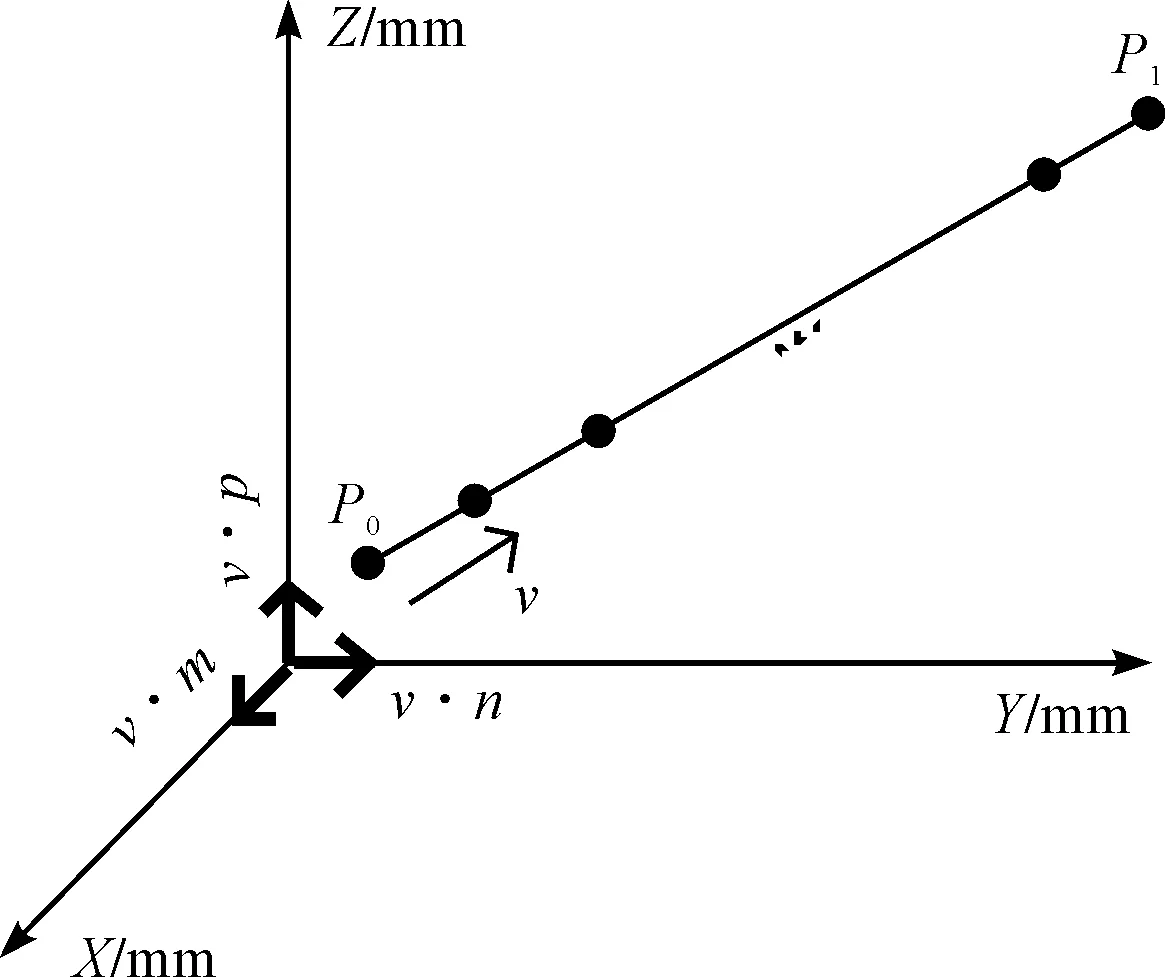
图4 利用速度时间关系计算轨迹准确度
理论直线方程为:
(13)
理论直线方向单位向量为(m,n,p),可由下式计算:
(14)
将测量数据进行等间距分段,对每段直线进行相同的分析处理,采样频率为t=0.01 s,可根据下式求出每两点之间速度:
(15)
将分段内的速度值进行最小二乘法拟合,即:
v=v0+at
(16)
式中:v0—初始速度;a—加速度;t—运动时间。
将其近似看成沿理论直线方向的运动速度,据此由下式求出分段内每个时刻在理论直线上对应位置为P0i(x0i,y0i,z0i):
x0(i+1)=x0i+vtm
y0(i+1)=y0i+vtn
z0(i+1)=z0i+vtp
(17)
轨迹位置误差如下:
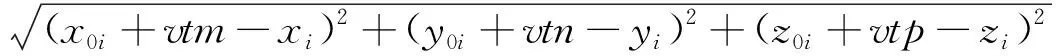
(18)
2 实验及结果分析
2.1 测试条件
首先笔者对工业机器人进行必要的校准操作;设定测试的环境温度为20 ℃,试验温度应保持在±2 ℃之内,并将实验装置置于试验环境中24 h[9-11]。
该实验所要测试的直线为点P2~P4。实验在10%额定负载(10 kg)、10%速度下进行测试,循环次数为10次,最终结果为10次循环的平均值。
2.2 实验结果
实验计算数值以激光跟踪仪为坐标系,P2点在激光跟踪仪坐标系下的理论值为(4 823.453 181 mm,-3 317.412 862 mm,1 163.644 51 mm),P4点在激光跟踪仪坐标系下的理论值为(5 017.637 83 mm,-3 689.241 917 mm,743.126 406 3 mm),激光跟踪仪采样频率为100 Hz,即t=0.01 s测一个点。
直线轨迹位置误差的3种计算方法结果如图5所示。
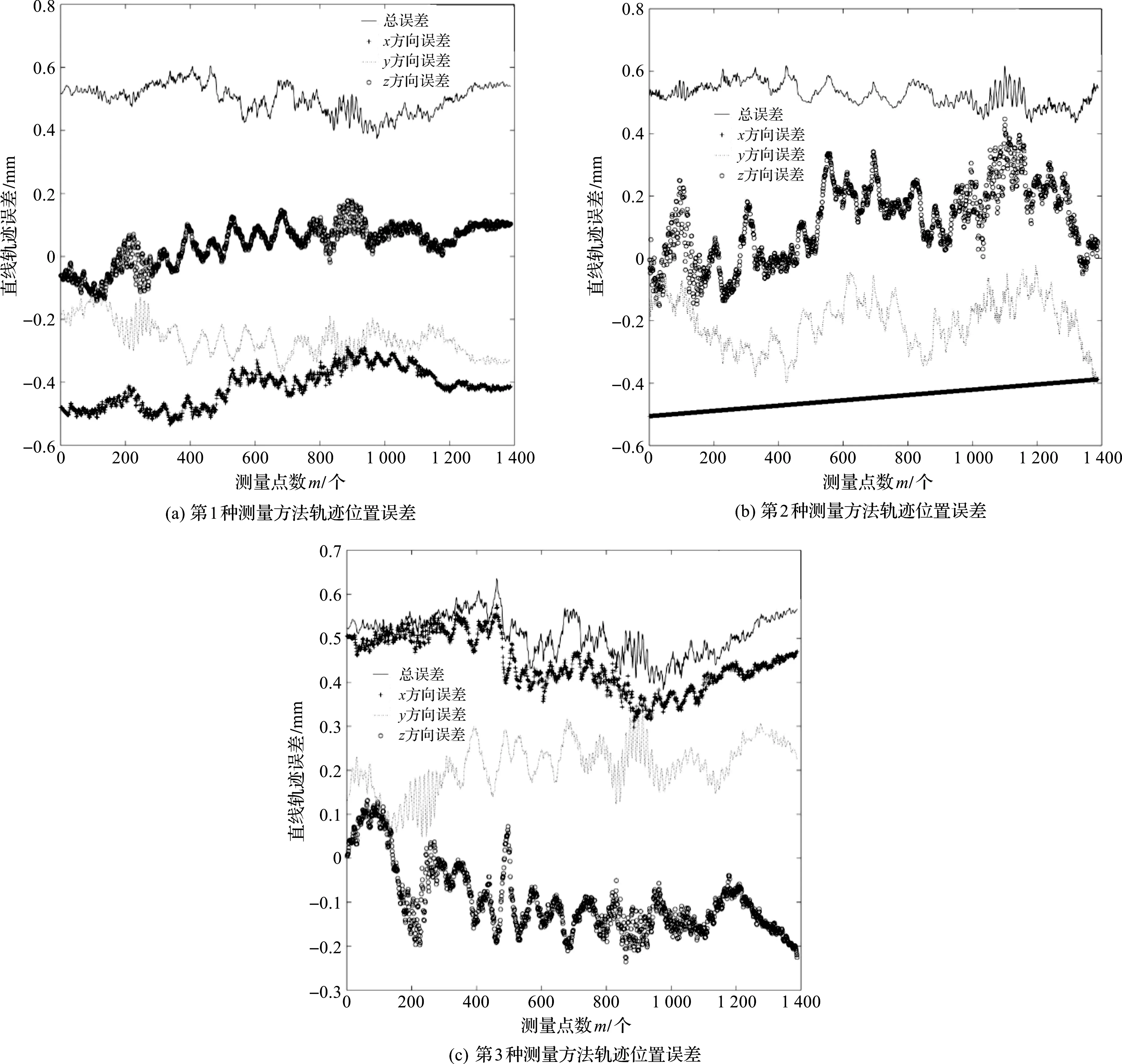
图5 3种测量方法直线轨迹误差测量
图5(b)中,第2种测量方法将x作为自变量,y、z作为x的函数,所以x方向的误差结果为一条直线。
3种测量方法的误差最大值、平均值、标准差如表1所示。

表1 3种测量方法的误差最大值、平均值、标准差
2.3 结果分析
由表1可看出,轨迹误差最大值最小为0.605 1 mm,轨迹误差最大值最大为0.636 0 mm;平均值最小为0.501 4 mm,平均值最大为0.525 6 mm;标准差最大为0.045 9 mm,标准差最小为0.035 8 mm,3种计算方法各有优缺点。
从图5中可以看出,3种计算方法整体上误差值变化有相同的趋势,误差变化幅度相似,x方向误差值比较大,z方向误差值比较小;3种计算方法都可以比较精准地对工业机器人直线轨迹位置误差进行评估,可为机器人位置误差补偿提供理论依据。
3 结束语
本文采用激光跟踪系统对工业机器人直线轨迹误差进行了测量,通过最小二乘法和样条、线性插值法等3种计算方式对测量数据进行了计算。3种方法都解决了国家标准中没有规定的应该构造多少正交平面以及应该放置它们的位置等问题。
此外,3种计算方法都很好地对机器人直线轨迹位置误差进行了评估,对机器人的轨迹误差补偿提供了理论依据。
