First-principles study on the mechanical properties and thermodynamic properties of Mo–Ta alloys

Xin ZHANG(张欣),Heng LI(李恒),Yuhong XU(许宇鸿),Qijun LIU(刘其军),Yangyang LIU (刘洋阳), Zilin CUI (崔子麟), Haifeng LIU (刘海峰),Xianqu WANG (王先驱), Jie HUANG (黄捷), Hai LIU (刘海),Jun CHENG (程钧), Ming LI (李明), Shaofei GENG (耿少飞),Changjian TANG (唐昌建),4 and Guangjiu LEI (雷光玖)

1 Institute of Fusion Science, School of Physical Science and Technology, Southwest Jiaotong University,Chengdu 610031, People’s Republic of China

2 School of Physical Science and Technology,Southwest Jiaotong University,Key Laboratory of Advanced Technologies of Materials,Ministry of Education of China,Chengdu 610031,People’s Republic of China

3 Southwestern Institute of Physics, Chengdu 610041, People’s Republic of China

4 School of Physical Science and Technology,Sichuan University,Chengdu 610065,People’s Republic of China

Abstract The mechanical properties, thermodynamic properties and electronic structure of Mo1−xTax(Mo–Ta) alloys (x=0, 0.0625, 0.125, 0.25, 0.3125, 0.5 and 1) were calculated by using firstprinciples.The electronic structure of Mo–Ta alloys was analysed by the projected density of states(PDOS).The low temperature heat capacity was estimated by Fermi energy and Debye temperature.It is shown that the formation enthalpy will decrease with the increase of Ta content, and the cohesive energy will increase with the increase of the Ta content.On the other hand,the addition of Ta atoms will reduce the strength and improve the ductility of Mo–Ta alloys,the Debye temperature will decrease and the low temperature heat capacity will be improved with the increase of the Ta content.All these results will be useful for the research of new plasma grid(PG)materials,which is mainly used in neutral beam injection (NBI) systems to produce negative hydrogen ions.

Keywords: first principles calculations, Mo–Ta alloy, mechanical properties, thermodynamic(Some figures may appear in colour only in the online journal)

1. Introduction

Recently, body-centred cubic (BCC) transition elements and their alloys have increasingly been the subject of research,especially regarding their mechanical properties due to their good physical and chemical properties, such as extreme stiffness, high melting point and high thermal conductivity. Henceitshould benoted that,these metals and alloys are receiving considerable attention as potential plasma facing material of the divertor and the first wall in fusion power reactors[1–6].On the other hand, molybdenum (Mo) and tantalum (Ta) are typical BCC transition metals.In particular,Mo is an electrode material used to make plasma grid in NBI system [7], and another potential electrode material is tungsten. In addition, more and more attention has been paid to the feasibility of using alloy materials to make electrodes. Alloying can significantly improve the physical properties of metals. Ham et al pointed out that Mo–Ta alloys may work at high temperatures and have high strength [8]. Mo–Ta alloys are good candidate for gate electrode applications due to the good thermal and chemical stability [9, 10]. Turchi [11] and Van Torne et al [12] studied the structure and mechanical properties of Mo–Ta alloys.However, they paid little attention to the elastic modulus,hardness and thermodynamic properties of Mo–Ta alloys.Compared with traditional methods of experimental investigation, DFT calculation is a good method for studying the properties of materials, especially mechanical and thermodynamic properties. The computational data can make reasonable prediction of the properties of materials, so the calculated results may serve as guidance for further experiments.Research costs will be greatly reduced by first-principles study.

Table 1.The k-point mesh,energy cut-off(eV)and calculated lattice constants of Mo1−xTax alloys(x=0,0.0625,0.125,0.25,0.3125,0.5 and 1).

In this work, the structure, stability, elastic properties,Debye temperature and low temperature heat capacity of Mo1−xTax(Mo–Ta) alloys (x=0, 0.0625, 0.125, 0.25,0.3125, 0.5 and 1) have been studied via first-principles. We can have a good understanding of the basic physical properties of these alloys due to these calculated results. On the other hand, these results will provide a useful database for relevant Mo–Ta alloy studies.

2. Computational methods and model

A method based on the DFT [13, 14] was used to study the mechanical and thermodynamic properties of Mo–Ta alloys,which was done using Cambridge Serial Total Energy Package Code (CASTEP) [15]. The ultra-soft pseudo-potential plane-wave (UPPW) [16] was used to describe the interaction between valence electrons and core ions and general gradient approximation(GGA)PBE[17]was used for exchange correlation. The Monkhorst–Pack method [18] was used for k-points sampling,as M×M×M.The values of M and the plane wave cut-off energy are shown in table 1. All these structures were fully relaxed until the forces exerted on all atoms are less than 0.01 eV Å−1[19].

In the references, Van Torne et al pointed out that the Mo–Ta binary diagram shows a continuous BCC solid solution across the entire diagram [12]. All of the structural models are depictived by the 2×2×2 supercell, which is containing 16 atoms in a BBC structure. Various alloys with different Ta concentrations were obtained because a portion of the Mo atoms were substituted by Ta atoms; those are pure Mo, Mo0.9375Ta0.0625, Mo0.875Ta0.125, Mo0.75Ta0.25,Mo0.6875Ta0.3125, Mo0.5Ta0.5and pure Ta. All of these structural models are shown in figure 1.

3. Results and discussion

3.1. Structure optimisation

First,the positions of Ta atoms in the supercell must be taken into account. Theoretically, Ta atoms can be placed in any position in the lattice when Mo atoms are replaced by Ta atoms to form Mo–Ta alloys such that the lattice structures of Mo–Ta alloys with the same Ta concentration are undetermined. Thus, we should confirm the energetically most favourable atomic arrangements of Mo–Ta alloys in a 2×2×2 supercell. All these structures in figure 1 are the lowest energy structures.As shown in figure 1,Mo–Ta alloys still retain the BCC structure, the Ta atom prefers to be in a position that ensures a high degree of symmetry throughout the lattice structure.

The calculated lattice constants of Mo1−xTaxalloys

(x=0, 0.0625, 0.125, 0.25, 0.3125, 0.5 and 1) are shown in table 1. The results of lattice constants had been overestimated because the GGA approach was used for geometry optimisation[22–25].Even so,the calculated lattice constants were in good agreement with the experiment data. Figure 2 shows the change trend of equilibrium lattice constants of Mo–Ta alloys with the increase of Ta content.

Figure 1. The energetically most favourable atomic arrangements of the BCC Mo1−xTax (x=0, 0.0625, 0.125, 0.25, 0.3125, 0.5 and 1)alloys in a 2×2×2 supercell. The cyan and red atoms are Mo and Ta, respectively.

Figure 2. The change trend of equilibrium lattice constants of Mo–Ta alloys.

3.2. The energy and stability of the Mo–Ta alloys

Formation enthalpy and cohesive energy are important parameters for evaluating the stability of alloys. The formation enthalpy and cohesive energy of Mo–Ta alloys are calculated according to the following equations:

where x is the Ta concentration,Etot(M o1-xTax),Ebulk(M o)andEbulk( Ta)are the total energy of Mo1−xTaxalloys (2×2×2 supercell), bulk Mo and bulk Ta (2×2×2 supercell) in the BBC lattice, respectively.Eiso( Mo)andEiso(T a)are the energies of an isolated Mo and Ta atom,respectively. N is the number of atoms. According to this definition, negative values of the formation enthalpy (Ef) andcohesive energy (Ecoh) mean that the formation of Mo1−xTaxalloys releases energy so that it is more thermodynamically stable. Table 2 shows the calculated results, and the changes of formation enthalpy and cohesive energy with Ta concentration are shown in figure 3. The formation enthalpy that has continuously decreased with the increase of Ta concentration,which means that Mo–Ta alloys formed by bulk Mo and bulk Ta become more and more thermodynamically stable with the increase of Ta content.According to the formation enthalpy, the Mo0.5Ta0.5alloy is the most thermodynamically stable. The cohesive energy of Mo–Ta alloys continuously increases with the increase of Ta concentration, which means that it becomes more and more difficult to decompose the Mo–Ta alloy into individual Mo and/or Ta atoms with the increase of Ta concentration.

3.3. The mechanical properties of Mo–Ta alloys

The elastic constants of every Mo1−xTaxalloy and the mechanical property parameters of every Mo1−xTaxalloy were calculated in this work. The elastic constants Cijare essential parameters that determine the response of the crystal to external forces and are related to the initial fundamental mechanical properties. Table 3 shows the calculated elastic constants,which are plotted in figure 4(a)as a function of Ta content. And there are only three independent elastic constants, C11, C12, and C44, for a body-centred cubic system.We have known that all of the Mo1−xTaxalloys are thermodynamically stable because all of the values of the formation enthalpy of Mo1−xTaxalloys are negative. According to the‘Born stability criteria’, we can understand the mechanical stability of cubic crystals. The ‘Born stability criteria’ are as follow [29]

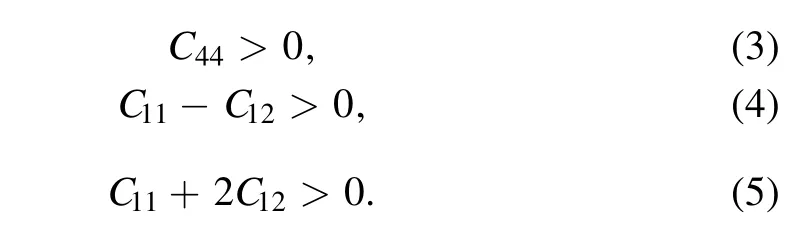
All of the Mo1−xTaxalloys are mechanical stable because they all satisfy these conditions.The elastic constants C11and C44continuously decrease with the increase of the Ta content.However,the change in elastic constant C12with the increase of the Ta concentration is not significant.Elastic constant C11is one of the most important parameters and is related to the stiffness. We can see that the C11value is monotone decreasing from 478.28 to 262.38, which suggests that more Ta content reduces the stiffness of the Mo1−xTaxalloy.

We can estimate the Cauchy pressure C12−C44[30],which can be used to describe the brittle/ductile properties of alloys.If the Cauchy pressure(C′)is positive,the metal bonds dominate the crystal, showing the ductility of the material[31].It is obvious that all Mo–Ta alloys have positive Cauchy pressure.

Figure 3.The changes of formation enthalpy and cohesive with the increase of Ta content.

The elastic moduli can be obtained using Voigt–Reuss–Hill approximation [32–34], which is a good method for evaluating the performance of materials from the calculated elastic constants. For cubic crystals, the bulk moduli (B),shear modulus(G),Young’s modulus(E)and Poisson’s ratio(σ) can be calculated from the following equations (6)–(11)[35] and are shown in table 4

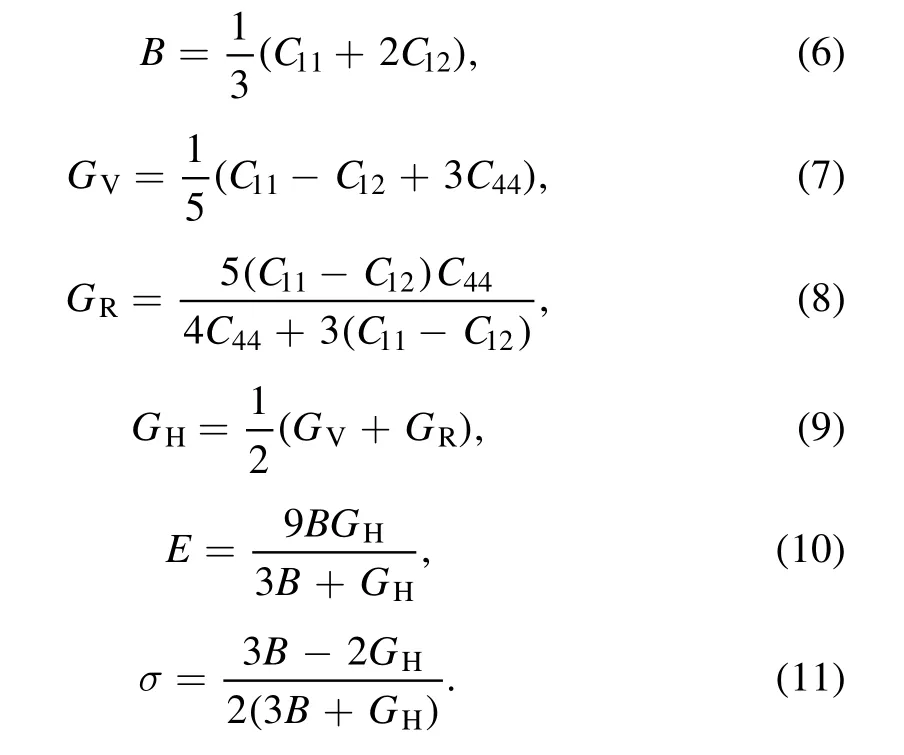
As we know,the elastic modulus represents the ability of bulk materials to resist external forces. From figure 4(b), it can be seen that the increase of Ta content will gradually reduce the elastic modulus. The larger the bulk modulus is, the greater the hardness is. Thus, pure Mo alloys have the greatest hardness. The simulation results show that the addition of Ta atoms will reduce the strength of Mo–Ta alloys.

Figure 4.(a) Elastic constants Cij of Mo–Ta alloys, (b) elastic modulus of Mo–Ta alloys.

Table 3. The calculated elastic constants Cij (GPa) of Mo1−xTax alloys.

Table 4.Elastic modulus (GPa), B/G ratio and Poisson’s ratio (σ, GPa) of Mo1−xTax alloys.

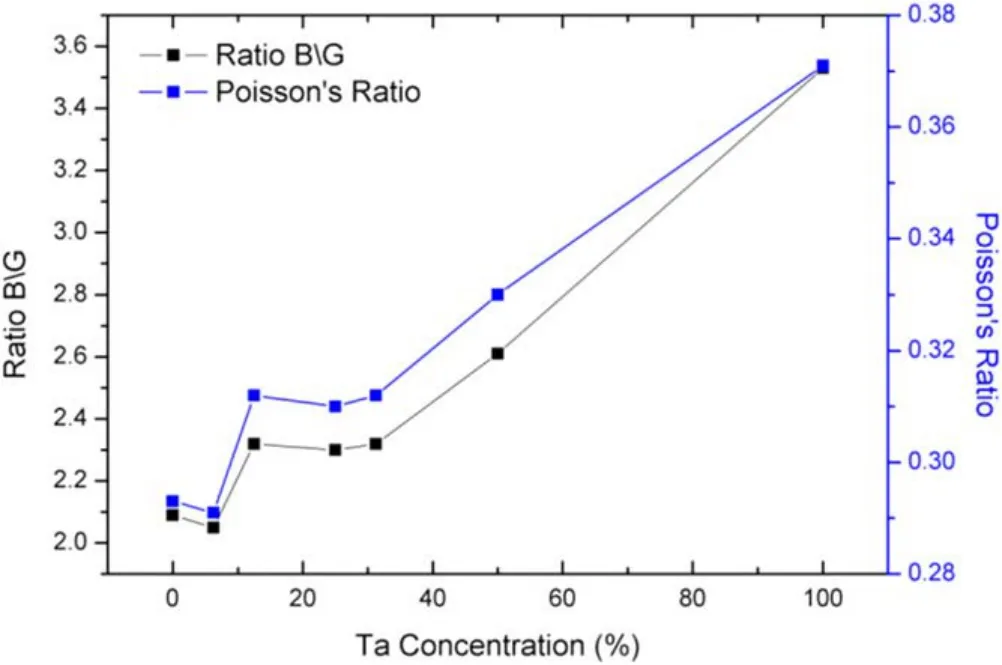
Figure 5. Poisson’s ratio and B/G ratio of Mo–Ta alloys.

The B/G ratio present the ductility of metal materials due to Pugh’s theory [36]. If the B/G ratio is less than 1.75, the material shows brittleness. Instead, materials exhibit ductility.It is obvious that the B/G ratios of all Mo–Ta alloys are larger than 1.75. The new rule given by Frantsevich et al [37] indicates that alloys can be considered as ductile material when their Poisson’s ratio (σ) is larger than 0.26. From figure 5, we can see that the B/G ratio and Poisson’s ratio show the same trend with the increase of Ta content. The ductility order of Mo–Ta alloys is: Mo0.5Ta0.5＞Mo0.875Ta0.125＞Mo0.6875Ta0.3125＞Mo0.75Ta0.25＞Mo0.9375Ta0.0625. Because the ductility of pure Ta is better than that of pure Mo, the ductility of mo–ta alloy can be improved by more Ta content.

3.4. The electronic structure

The electronic structure of Mo–Ta alloys can be analysed by the projected density of states (PDOS). In this paper, the PDOS of Mo0.9375Ta0.0625, Mo0.875Ta0.125, Mo0.75Ta0.25,Mo0.6875Ta0.3125and Mo0.5Ta0.5are presented in figure 6.We can see a pseudo-gap at the Fermi level, which is a characteristic of typical transition metal alloys. The bonding valence electrons are mainly distributed in the energy range of−5–20 eV. Compared with the pure Ta metal, theTa-containingalloys reduce the energy level of Ta states.Compared with the PDOS of Mo far away from Ta,the degree of overlap of Mo states and Ta states is higher when Mo atoms gets closer to Ta atoms. This may be due to the difference in electronegativity between Mo(2.16)and Ta(1.50),which can cause a small charge transfer between Mo atoms and Ta atoms. And figure 6 also demonstrates the degree of overlap of Ta states and Mo states in the case of Mo0.5Ta0.5is the highest, showing the Mo–Ta bonding strength is the highest in Mo0.5Ta0.5.

3.5. The thermodynamic properties of Mo–Ta alloys

3.5.1.Debye temperature. Debye temperature is an essential parameter for materials, which corresponds to the highest frequency of lattice vibration and indirectly reflects the strength of the binding force between atoms. Debye temperature can be estimated using the following relationship [37]:

where ρ, h, kB, NA, M and n are density, Planck constant,Boltzmann constant, Avogadro constant, the weight of a supercell and the number of atoms per formula, respectively.Vl, Vtand Vmrepresent the longitudinal sound velocity, lateral sound velocity and average sound velocity, respectively. From table 5, we can see that the Debye temperature of 466.5 K of pure Mo decreases to 228.8 K for pure Ta,which indicates that the binding force between atoms is strongest in pure Mo.

3.5.2. Low temperature heat capacity. The low temperature heat capacity can be estimated by Fermi energy and Debye temperature, which are defined as follows:

For the above formulae, EFis the Fermi energy,ħ is reduced Planck constant, m is the electron weight, and ρeis the electron density of Mo–Ta alloys.γ and β are the electron and phonon heat capacity coefficients, respectively. N is the number of valence electrons of Mo–Ta alloys,5 s1for Mo and 6 s2for Ta. R is the molar gas constant, Cvis the heat capacity, and T is the temperature.

From formula (19), the heat capacity is divided into two parts: the electron and phonon heat capacity. Obviously, the larger the value of γ or β is,the larger the heat capacity is. As shown in table 5, the value of γ or β continuously increases with the increase of Ta content such that heat capacity also continuously increases, as shown in figure 7. From formulae(16) and (17), we can find that the magnitude of γ is mainly determined by the number of valence electrons.This is because only the valence electrons, which are near the Fermi level and have a high probability of being excited, will contribute to the heat capacity. Undoubtedly, More Ta atoms lead to more valence electrons.

Table 5.The density ρ(g cm−3),longitudinal sound velocity Vl(m s−1),transverse sound velocity Vt(m s−1),average sound velocity(m s−1),Debye temperature (K), low temperature parameters of the electron heat capacity coefficient γ (J/(mol K2)) and phonon heat capacity coefficient β (J/(mol K4)) of Mo–Ta alloys.

Figure 7. Low temperature heat capacity of Mo–Ta alloys.

Acknowledgments

This work was supported by National Natural Science Foundation of China (No.11820101004), the National Key R&D Program of China (2017YFE0300100, 2017YFE0301100).