让学生学会“问题解决”的策略

严 伟 （江苏扬州高新区实验小学）

在数学“问题”解决中，关键在于对“问题”的分析：给出了哪些条件（已知），求解哪些数值（未知），怎样来选择解题思路（解答过程）。在策略选择上，教材中涉及的有分类讨论、数形结合、等价转化、归纳等方法。要引导学生立足“问题解决”来选择正确的解题策略。

一、用数学思维来面对“问题解决”题型

解决数学“问题”需要用数学思维。很多时候，我们在教学中，往往关注解决问题的方法，忽视对学生“问题解决”思维的启发和培养。面对数学“问题”，为什么要这样解？数学思维的形成为解决“问题”提供了指导，也为学生把握问题创造了条件。平时，在解数学问题时，很多学生习惯以“即兴思维”来解题。如在六年级数学“找规律”问题中，有六个点，问可以连几条线段？有八个点，问可以连几条线段？在面对该题时，很多学生会选择“即兴思维”，在纸面上画出六个点，然后进行连线，最后数一数有多少条。如果换成八个点，也采用同样方法。显然，对于该类题型的求解策略应该是指导学生从简单问题进行分析，总结规律，再应用到相对复杂的问题解决中。也就是说，对于该“问题”的解决需要学生能够跳出“即兴思维”窠臼，运用数学的思维，分析“几个点之间连线的条数”问题。数学思维是解决数学“问题”的基本导向，在解决“问题”策略上，要培养学生理性思考“问题”的能力，运用数学思维来归纳出解题的具体策略。所以，对n 个点之间连线条数的计算，其解题思维为：S=1+2+3+…+（n+1）。通过启发学生的数学思维增强学生“问题解决”能力。

二、运用数学思想来指导“问题解决”的方法

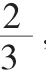
三、运用数学反思提升学生数学解题能力

解决“问题”只是数学教学的一个组成部分。面对数学“问题”，教师要鼓励学生从“问题”中进行反思，反思是否还有别的解决“问题”的方法，反思如果其他条件变化了，解题方法是否依然通用。如某题中：小明和小花共有72 枚邮票，小花比小明多12 枚，问两人各有多少枚邮票？最常规的解法是引入“画图”法，根据小花与小明邮票数量的关系来找出解题方法。但是否还有别的更好的解法？通过反思，我们可以假设两人邮票一样多，小花36 枚，小明也是36 枚，再根据小花比小明多12枚，将小明的36 枚减去12 枚，小花的36 枚加上12 枚，即可完成，这里所用的策略是“假设”法。所以说，在面对数学“问题”时，要通过解题引领学生反思，探寻更优、更好的解题策略，促进学生数学解题思维的进一步升华。

总之，在“问题解决”策略上，先要认真审题；接着，理解题设条件与求解问题之间的关系；然后列出求解过程，最后是反思该类问题，把握解题思想。