反应堆中子学屏蔽计算软件Hydra-SN3D的改进

明平洲,唐松乾,安 萍,芦 韡,刘 东,余红星

(1. 中国核动力研究设计院设计所,四川 成都 610213；2. 中国核动力研究设计院核反应堆系统设计技术重点实验室,四川 成都 610213)

中子、光子、电子等一些粒子可以导出波尔兹曼微分—积分守恒方程，统一被称为输运方程。核反应堆工程领域的辐射屏蔽输运计算主要表现为中子、光子等的物理参数求解。输运分析计算程序的核心，涵盖了几何、物理方法、核数据等多方面。现有的反应堆中子学输运程序使用分治策略，例如提供堆芯级别(Core Level)和栅元级别(Lattice level)这种主要分类计算形式[1]。Hydra-SN3D软件是由中国核动力研究设计院和西安交大研制的SN方法输运计算软件，使用源迭代法求解离散后的稳态粒子输运方程，在多种差分格式基础上使用KBA并行算法实现空间网格的并行扫描计算。该软件内部计算核心为类似于DORT和TORT等知名软件的核心输运求解器，外围则逐步集成较多的辐射屏蔽计算功能，例如中子/光子耦合计算功能[2-3]。

1 数值方法

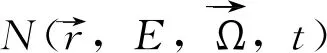
1.1 SN方法

中子或光子的辐射效应通常由波尔兹曼输运方程的离散纵标(SN, Discrete Ordinates)形式进行建模，它的主要特点在于空间角度的离散。

Ωm·Img+(σA+σS)Img

(1)

辐射通量Img(x,y,z)按照能群、角方向进行离散化，公式表明沿着一个特定方向Ωm辐射通量发生的变化，求解过程便是定量获得此变化趋势。该近似方法是把变量Ω直接离散的数值方法，即只对选定的若干个离散方向Ωm对中子输运方程求解。从中子输运方程求出φ(r,E,Ωm)后，关于方向Ω的有关积分则用数值积分来近似表示。

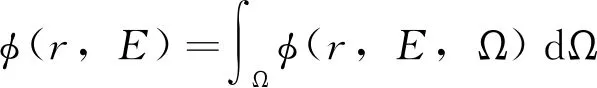
(2)

式中,求积系数ωm、离散方向及其数目取决于计算精度的要求，这便构成离散纵标法(SN方法，又写作SN)。此处下标N表示方向向量在某个纵坐标方向上(例如直角坐标系的x方向坐标轴)的离散点数目。在反应堆物理和屏蔽计算中，对中子角通量密度分布各向异性比较严重或非均匀性比较强烈的问题(例如栅元或燃料组件)的计算中都广泛应用[4]。文献归纳SN数值方法求解中子输运方程的主要问题为：

1)角度方向的离散、数目及求积组的选取；

2)针对空间、方向变量的中子输运方程的离散化方法及离散方程组的获得；

3)离散方程的合理求解，包括加速收敛等。

以简化形式书写多群近似中子输运方程：

Ω·φg(r,Ω)+∑t,gφg(r,Ω)=Qg(r,Ω)

(3)

在选定求积组(Hydra-SN3D软件默认使用全对称求积组，也可以输入其他类型的求解组)之后，对每一个选定的离散方向附近区域进行积分，可以得到对应的离散方程：

[Ω·φ(r,Ω)]m+∑tφm(r)=Qm(r)

(4)

实际上对于不同的坐标系统，式(4)的求解具有不同的离散表达式。常使用的是直角坐标系(x,y,z)和圆柱坐标系(r,φ,z)进行确定论的SN方法推导。

1.2 外推模型

空间变量在中子输运方程中含有空间变量的导数又含有对方向向量的导数，所以空间变量兼具曲几何和直角坐标系的特点，在离散过程中将产生对应的外推模型[5]。

(1)菱形差分

针对每一个网格，以二维情况为例，(i,j)网格中守恒方程含有φi,j,m,φi±1/2,j,m,φi,j±1/2,m等五个未知函数，曲几何还需要加上φi,j,m±1/2两个未知函数，共7个未知数。菱形差分便是补充式(5)所示的关系式，便于使用待定系数法来求解这些未知函数。

(5)

其他维度或方向上有类似的菱形差分格式，公式表明网格入射中子角通量密度与出射中子角通量密度具备线性关系的连续性。

(2)带权菱形差分

菱形差分近似认为网格中心的中子通量密度和网格表面中子通量密度按照直线变化，带权菱形差分则使用更为一般的线性关系来表示它们之间的关系。

φi,j,m=0.5(1+a)·φi+1/2,j,m+ 0.5(1-a)·φi-1/2,j,m

(6)

(3)阶跃近似

对于每个维度或方向上，对带权菱形差分使用特定的系数，此时对应于阶跃近似。

(7)

式中:μm——方向余弦。

(4)θ加权菱形差分

该模型得到的结果更接近线性结果，使用可调节几何外推参数γi(θ)来代替一般线性关系中的系数。

φi,j,m=γi(θ)·φi+1/2,j,m+(1-γi(θ))·φi-1/2,j,m,0.5≤γi(θ)≤γi(θ)≤1.0

(8)

θ(0≤θ≤1)作为用户输入参数，用于调整网格内通量分布的形状。θ在DORT/TORT程序内的建议值为0.9。Hydra-SN3D软件同样将权值默认取为0.9，也可以由用户输入文件进行读取。

1.3 核数据

在Hydra-SN3D软件内核数据指代的是问题独立的多群输运常数截面数据，Hydra-SN3D软件存放截面数据的文件遵循ANISN格式，它由TRANSX接口程序对基本的多群常数库进一步处理得到计算所需的输运截面。实际计算过程中这些核数据参数按照FORTRAN编程语言提供的UNFORMATTED格式进行组织，可以对基准例题提供的输运截面参数进行手动填写或者使用TRANSX接口程序自动生成。Hydra-SN3D软件具备上散射输运计算和输入高阶散射截面的功能[6]。

2 Hydra-SN3D的改进

根据Hydra-SN3D软件的实际使用情况，进行以下两个方面的改进：一方面是提升输入文件在读取过程中的容错性；另一方面是进一步提升计算效率。

2.1 前处理

Hydra-SN3D软件的输入文件按照FIDO格式进行提供，用户填入内容相对比较自由，但缺乏容错性的支持，当用户提供明显错误的输入时软件将正常执行而不会报错退出。对Hydra-SN3D软件的改进策略之一便是重新设计输入文件形式，使用Python脚本编程语言书写前处理模块，判断输入数据的不合理内容，提升软件本身的容错性(见图1)。

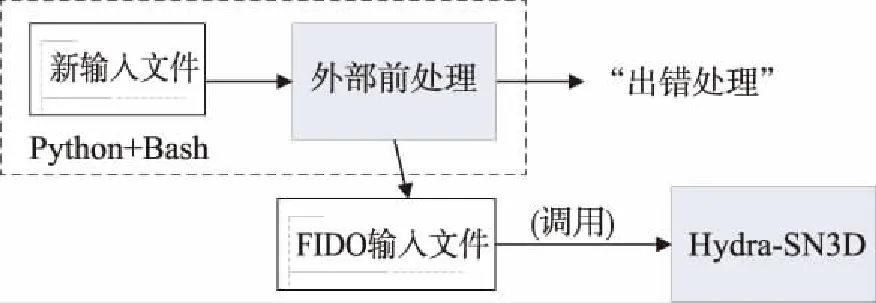
图1 外部前处理的改进策略Fig.1 Improvement strategy of external pre-processing

新的输入文件格式命名为NAC(Numerical Arithmetic Context)，采用类似于互联网应用常使用的JSON方式的统一格式，利用层级关系来表达文本信息。输入文件格式强调以数据块名称进行区分，在每个数据块内可以包含各种基本数据类型及其值，例如单变量或数组变量等。为了提升易用性，每个数据块的数据格式至多支持三级结构，每级结构的数据块名称不能重合，不同级的数据块名称可以重合，访问时按照A∶B∶C这种方式来显式说明，表1的示例中数据块Test1中变量var1有两个，访问时分别为Test1∶var1或者Test1∶var5∶var1。

表1 NAC输入文件格式示例

各个数据块在使用Python编程实现时可以按行顺序读取，也可以按照变量名称选择性读取，正则表达式等机制则应用于关键字或数值的匹配。为了与数值计算部分有效连接，在Hydra-SN3D软件的改进过程中使用Python外处理过程读取新的NAC格式的SN计算输入文件，共计约40个变量。这些变量的值分为单数据或者数组数据两种情况，读取完成后然后进行容错性判断，隔离基本的输入错误或者一些不合理的输入(例如截面数值小于0，堆芯材料布置异常)，然后自动生成旧的FIDO格式输入文件，同时链接Hydra-SN3D软件执行运算。这种方案提升了计算用户建立输入文件的效率，且部分错误在执行Hydra-SN3D软件之前便由新的前处理进行了隔离。与此同时，NAC输入文件格式还具备耦合前处理的能力，即将数值计算部分作为库的形式进行耦合，使用Python-SWIG将Python读取的输入文件数据传递给数值计算的编程语言部分(通常为C/C++或FORTRAN)，实现内耦合的技术目标，可以应用于堆芯物理-热工耦合数值计算[7]。

2.2 多级并行

SN方法在结构化网格的条件下有着著名的KBA并行扫描算法[2,8]，Hydra-SN3D对波尔兹曼输运方程在方向和角度离散化之后的数学方程进行合并，构造所有通量矩的线性系统来进行扫描计算。

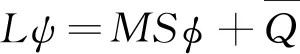
(9)

φ=Dψ

(10)

L——差分输运算符；

M——通量矩离散化算符矩阵；

S——散射矩阵。

待求解对象ψ代表角通量;

φ为通量矩。XYZ三维结构化网格情况下KBA扫描计算的实质是求解L-1，它将三维网格进行二维划分，总的网格在每个方向上为(I,J,K)，每个区域(Ia,Jb,K)映射至每个MPI进程进行并行求解。整个扫描计算过程对每个卦限进行各个离散方向的网格扫描求解通量矩和角通量信息。假定整个结构化网格被区域分解为5×2，在第一卦限内进程之间具有如图2所示的波前网格区域扫描结构。进程9首先进行计算，进程4和进程8接收到进程9发送的边界数据后可以并行计算。

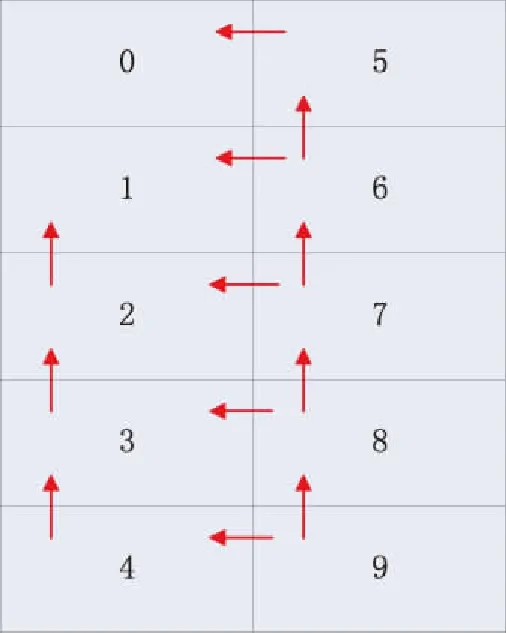
图2 多进程通信示意图Fig.2 Schematic of multi-process communication

按照文献给出的数据，理论的并行效率与较多输入参数相关，例如每个卦限内离散角的数量变化由S4到S32，相应的并行效率变化范围可以达到0.75到0.99[3]。这里对Hydra-SN3D软件的KBA并行扫描算法增加OpenMP并行算法，借鉴文献[8]给出的MPI-OpenMP-SIMD多级并行在SN方法中的应用，本算法编程实现时将依序对多个卦限内XY方向上的扫描计算循环增加OpenMP编译指导语句，即在已有MPI多进程运行的基础上添加多线程并行。以第一卦限内XY方向上的扫描计算为例，算法描述见表2。

表2 多线程并行算法的描述

在上述计算过程中，菱形权重差分外推模型的计算子函数T具备独立性，仅仅与网格序号(i,j,k)相关。通量矩变量φup、φpsi等存在着先后依赖关系，因此径向(i,j)的扫描具备流水线结构。引入计算是否完成的标志位二维数组，其维度为(j,i)，每个维度的大小与扫描计算所需的上一个维度数据φup,j相同。每个线程在实际执行计算之前判断标志位done，当标志位表示数据已就绪，则马上执行计算；当标志位表示数据还未提供，则线程阻塞。计算子函数T在Hydra-SN3D软件内是FORTRAN编程语言书写，为了实现数据一致性，多级并行方案首先进行C/C++编程语言的等价转换，调整数据结构易于多线程并行；然后将外推模型的计算进行局部扩展，辅助展开流水线结构的计算语句。整个多级并行的编程实现命名为NAC4R，它将在数值验算部分给出性能的对比。

3 数值验算

对Hydra-SN3D软件的改进涉及程序代码的转换、结构的调整和多级并行编程，这里使用三个计算问题来对软件进行完整验算，确保计算与改进之前的结果一致，且同时验证前处理的正确实现。整体运行环境使用单个节点具备20个处理器核心的集群计算机。如表3所示。

表3 计算例题说明

在集群上对Hydra-SN3D(MPI多进程并行)运行上述三个例题，图3中显示了它们的计算时间开销，纵轴计算时间取LOG10对数来反映加速趋势。

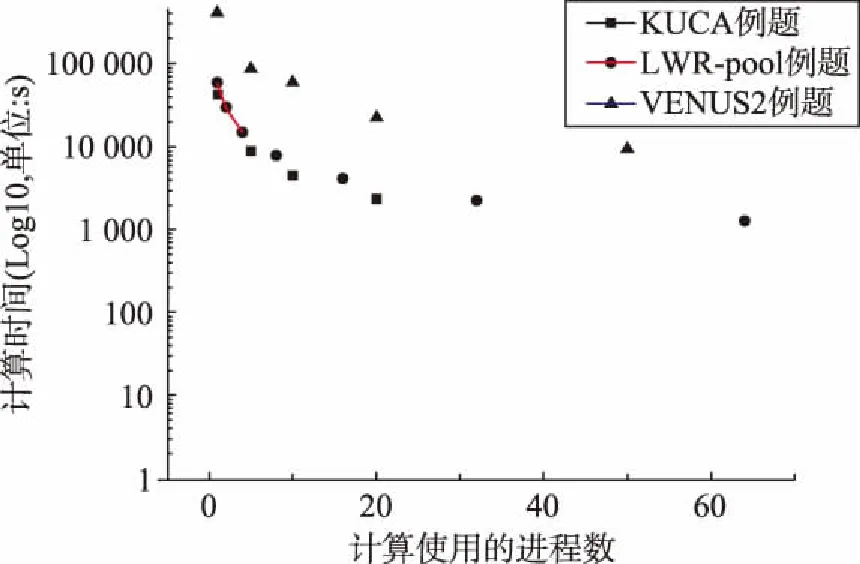
图3 源Hydra-SN3D软件的多进程运行统计Fig.3 Statistics of multi-process operation of Hydra-SN3D

这里也对每个例题的通量分布进行可视化，数值验算过程逐一对比了串行结果和并行结果，由于串行运行和并行运行的结果相同，因此仅绘制出串行运行情况的通量分布来表明未省略该验算步骤。如图4所示。

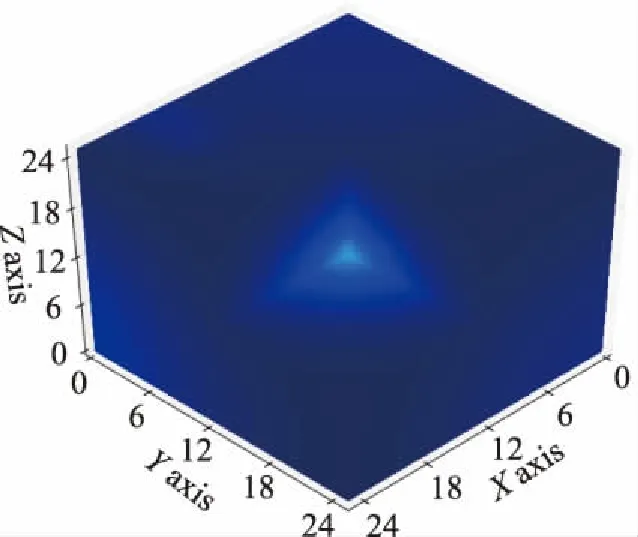
(a)KUCA例题的通量分布(g=1)

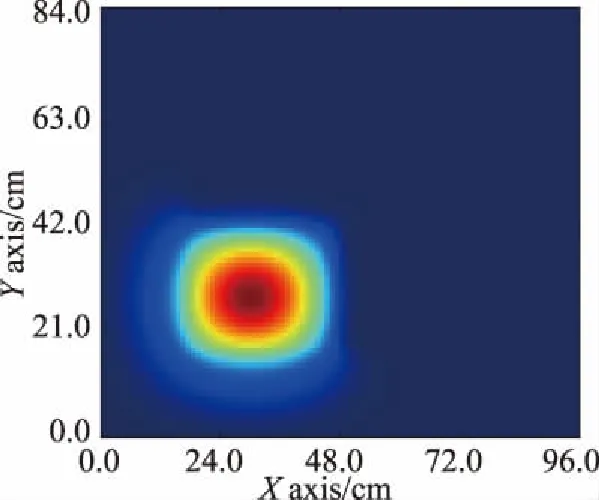
(b)LWR-pool例题的通量分布(g=1)

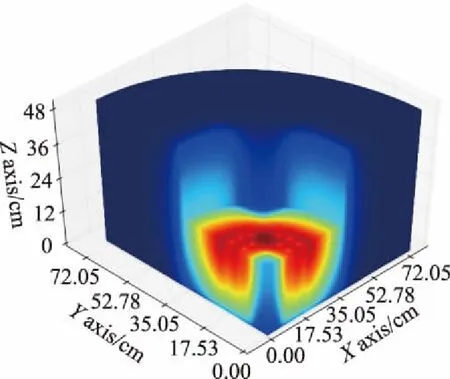
(c)VENUS2例题的通量分布(g=10)

分析1：原始的Hydra-SN3D软件使用MPI多进程并行，它在各种规模例题下存在着不同的加速特点。从计算结果来看，单个MPI进程运行时Hydra-SN3D软件的效率较低，结构化网格导致的对称性使得多进程并行可以通过不同的(Ia,Ib)组合来取得更好的多进程并行增益。KUCA例题使用100个进程的加速比为62.4，LWR-pool例题使用64个进程的加速比为45.6，VENUS2例题使用100个进程的加速比为80.1。

多级并行方案NAC4R存在着两个并行层次，第一个层次是对MPI并行部分重新组织数据结构，更快速地实现区域分解的MPI多进程并行；另一个层次是在径向扫描计算过程中引入OpenMP多线程并行，增强局部计算效率。这里对KUCA例题和LWR-pool例题这两个结构化网格对象的计算效率进行统计，观察OpenMP对计算效率的进一步改善情况。如表4所示。

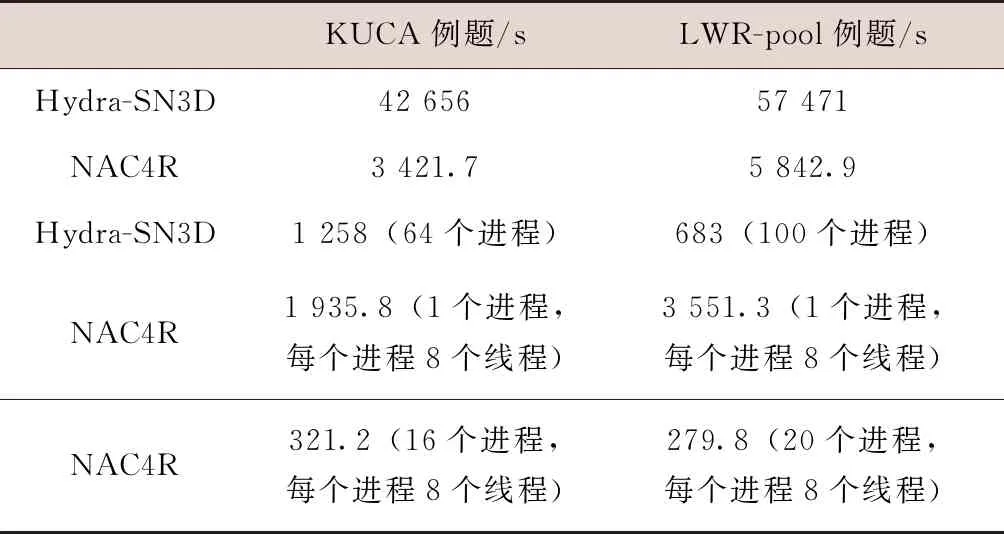
表4 多级并行的计算时间统计

分析2：通过程序改写和数据的重新抽象和组织，单进程的计算效率得到了较大提升，整体性能提升了一个数量级。对于每个基准例题，对每个进程使用8个线程实施的多线程并行均起到了加速的作用，KUCA例题和LWR-pool例题相比源Hydra-SN3D软件的运行结果，加速比分别达到132.8和205.4。此外统计两个例题使用一个进程联合8个线程的计算效率，可以得到各自的线程加速效果为1.8和1.6，这表明计算资源充足的情况下流水线扫描结构的多级并行能够取得更高的性能增益，且能够使用更多的计算资源。

验算过程中也对比了串行结果和并行结果，引入OpenMP并行之后的多级并行结果与原始的Hydra-SN3D软件运行结果保持一致。

4 结论

在Hydra-SN3D的应用过程中持续对该软件进行发展和改进，一方面对已有的前处理部分进行了改进，重新设计输入文件及其前处理流程，提升计算的容错性，自动检查计算用户输入参数的合理性；另一方面对Hydra-SN3D的编程语言实施等价变换和结构改进，提升单进程的运行效率。提出并实施多级并行算法，验算过程论证了整体计算效率的提升情况(均取得一个数量级的提升)。随着后续堆芯数值计算研究工作的开展，将借鉴解决此类特征问题的思路，引入形式化方法，对更多堆芯数值算法进行优化、改进。此外，流水线并行扫描结构存在于较多的堆芯数值计算过程中，其加速效果存在着IJ/(I+J+1)的理论推导，如何在实际软件编程实现中逼近这一理论上限和取得更好的增益将是下一步的技术研究重点。