结合PCNN与STF的老旧水利工程蓝图修复

刘 洋，刘雪芹，梁云辉，李学德

(江苏省水利勘测设计研究院有限公司，江苏 扬州 225217)

1 概述

图像修复是根据图像退化提出的一种图像处理技术，造成图像退化的原因有很多种，比如说，传感器的非线性性，光学成像系统的几何畸变与噪声干扰，图像运动造成的运动模糊，图像保存年代久远等等。

在每个工程竣工后，需要将工程竣工图纸打印晒蓝后存档，在经过很长时间保存后，蓝图中的线条会逐渐变淡或消失，如图1所示，进而影响借阅人对图纸的使用，因此若发现此现象，需要对图纸进行复原，因此，本文针对这种图纸退化提出了PCNN与STF结合的退化增强方法。

传统PCNN的方法是，利用PCNN集体点火的特性定位退化点，进而利用传统的非线性滤波器对退化点邻域进行滤波。然而，无论采用哪一种非线性滤波器都不能保证具有普适性，由于STF能够包含一切非线性滤波器，通过最优化的方式，对PCNN定位的退化点邻域内找出最适合的非线性滤波器，但是STF需要多次迭代，运算速度缓慢，因此在保证复原效果的基础上，通过图像退化点邻域局部扫描方式来加快运算速度。最后，通过计算信息熵和PSNR值，对图像进行滤波时不可避免地要破坏源图像的细节，这样，通过计算复原后的图像信息熵，可以对传统PCNN方法和本文提出的方法进行对比，好的方法必然带来低的信息熵值。而PSNR是最普遍，最广泛使用的评鉴图像质量的客观量测法，不过高PSNR值与高视觉品质无法挂钩，因此，本文仅仅用作参考。

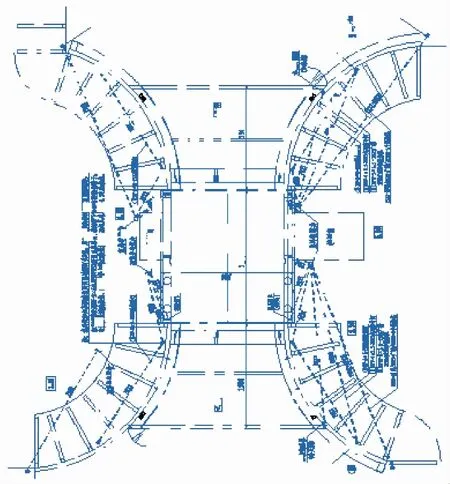
图1 老旧水利工程图纸退化图

2 PCNN

2.1 PCNN背景介绍

PCNN[1- 2]出现之前，Echorn[3]等人对猫科动物的视觉皮质研究时发现视神经活动具有同步动态性，提出了一种Echorn的视觉皮质模型。PCNN的特点与这一模型有着相同的特点，也就是具有相同输入的神经元会几乎同步的输出脉冲，因此，PCNN被认为是Echorn模型的剪裁和简化版本。PCNN被学术界称为第三代神经网络，其显著特点就是不需要繁复的训练过程，然后PCNN需要配置的参数非常多，需要经过大量的实验来确定PCNN的参数，稍后将介绍Yuli Chen等人[4]的PCNN做分割[5]的自动参数设置的方法，这种方法利用图像的先验统计概率知识对参数进行有效估计，与大量实验相比具有事半功倍的作用。

2.2 PCNN简化模型

PCNN是由脉冲耦合神经元(Pulse Coupled Neuron，PCN)组成的，每一个PCN由三个部分组成：输入域，调制域和脉冲发生器，如图2所示。每一个PCN从输入域接收信号，输入域又分为连接输入区和反馈输入区，每一个输入区有不同的突触和不同的时间常数，信号经过输入域后进入调制域，调制域对输入信号进行加乘耦合。最后信号送入脉冲发生器，脉冲发生器可以看作一个阶跃函数。

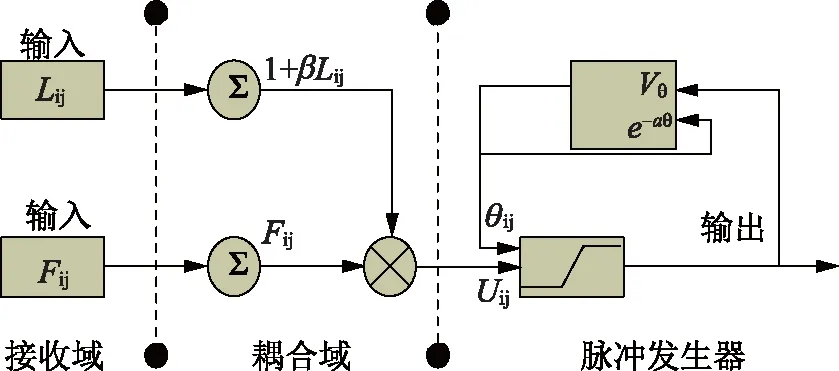
图2 脉冲耦合神经元(PCN)

本文提出的方法使用K.Zhan等人[6]提出的PCNN的简化形式突变皮质层模型(Spiking Cortical Model， SCM)，这种PCNN模型兼具计算复杂度小和运算速度快的特点，SCM可用如下所示的离散数学形式表示：

Uij[n]=e-αfUij[n-1]+

(1)

(2)

Eij[n]=Eij[n-1]+VEYij[n]

(3)

式中，Uij，Sij，Eij，Yij—神经元(每一个灰度图像像素对应一个神经元)的内部活动项，外部输入刺激，动态阈值以及点火输出；αf—指数衰减常数；W矩阵—神经元之间的连接权值；VL、VE—连接输入和动态阈值的幅值常数；β—连接强度常数。

本文的算法对SCM做了一点改变，有两处和SCM不同，一处在公式(2)所列出的点火函数，为了进一步加快运算速度，舍弃了sigmoid点火函数，采用传统的线性点火函数，另一处在公式(3)，省去了动态阈值的指数衰减常数。使每一个神经元有且只有一次点火。

2.3 PCNN常数自动获取方法

本文提出的算法，PCNN用作退化点挑选功能，如上节所述，一共有5个常数需要设置，分别是αf，W，VL，VE，β。Yuli Chen等人提出的理论有力的解决了这个问题，虽然上述文章将之用作分割，但是在选取退化点方面同样使用。这里省略原文的理论分析过程，直接给出利用先验知识获取的常数值，它们的数学表达形式如下：

(4)

(5)

VL=1

(6)

VE=e-αf+1+6βVL

(7)

β=0.1

(8)

其中σ(I)是输入图像的方差，而W的权值有所更改，本文的算法使用弱权值连接，以保证退化点在第一时间被挑选出来，β的表达式比较复杂，由于算法对β的要求不是很高，因此任意选取了一个值。

3 层叠滤波器STF

3.1 STF背景描述

在1986年，P.D.Wendit[7]等人基于信号恢复提出了层叠滤波器，层叠滤波器是由一系列正布尔函数(Positive Boolean Functions，PBF)构成的，因此它能组成各种现在广泛运用的非线性滤波器，如中值滤波器，非线性均值滤波器，排序统计滤波器等等。不过只有通过一系列迭代过程获取PBF的输出值，才能得到最优化的层叠滤波器，但是必要的时间花费，可以获得更好的图像恢复效果。

3.2 STF基本概念与局部扫描

3.2.1阈值分解函数

假设s是一幅灰度图像，Xl(s)是阈值分解函数，X(s)是阈值分解之后的图像，假设图像s的最高灰度级为M，STF第一步阈值分解可以表示为：

3.2.2PBF函数

PBF函数满足多对一的映射：f:{0，1}N→{0，1}即任意N维布尔序列映射到一维布尔序列，并且PBF函数具有层叠特性：x≥y→f(x)≥f(y)，这里，x和y都是N维向量。

本算法拟使用线性可分PBF函数，下面给出线性可分PBF函数定义：

(11)

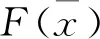
(12)

(13)

(14)

这里N代表STF的移动窗的大小，本文采用的窗口大小为7，窗口过小会导致退化恢复过度，窗口太大会导致大量细节被模糊化，因此采取比较适中的7窗口。

3.2.3基于PBF的STF定义与最优化方法

STF其实就是一个建立在PBF基础上的移动窗口滤波器，其表达形式如下：

(15)

tl=Xl(s)

(16)

在本文中求解PBF的目标函数是最小平均绝对值误差(Minimized Mean Square Error，MSE)，其表达形式如下：

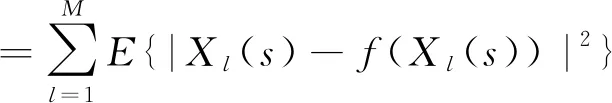
(17)

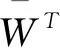
3.2.4局部扫描方法减少运算量

由于此种STF方法是对全局图像进行处理，进程十分缓慢，我们将利用PCNN定位的退化点，进行局部扫描，意思就是仅仅对退化点周围5×5范围内的图像进行STF最优化滤波，大大减少了运算量。由于5×5范围的图像中有可能包含不止一个退化点，我们将使用图39个模板(中的几个来进行滤波，挑选模板的原则是该模板仅仅包含我们当前处理的一个退化点，对于处理后的结果取中值代替原来的退化点即可，假设有n个模板符合要求，那么处理的结果表示为：

STFmedian=median{STF1，STF2，…，STFn}(18)

图3 TF滤波所用模板

4 实验算法与测试结果

4.1 算法与流程图

在本文之前，有很多基于PCNN的滤波算法，比如马义德等人[8]和石红美等人[9]的PCNN模型，使用了PCNN与传统线性或者非线性滤波器的结合，以往的实验结果说明非线性滤波器具有更好的滤波效果，在滤波的同时能更多的保存图像的边缘信息，不至于过度模糊化。而本文提出的算法使用了统一的非线性滤波器STF，以小小的时间代价避免了单一非线性滤波器带来的误操作。使用STF滤波的例子也很多，比如Anwtasios N. Venetaanopoulos[10]等人提出的最优多层层叠滤波器图像恢复算法，Jaakko T. Astola[11]等人提出的自适应层叠滤波器算法，本文使用层叠滤波器与上述不太一样，仅仅对局部区域进行扫描，这样不仅大大减少了运算时间，而且使图像得到最大面积的有效保护，下面给出算法的基本流程图，如图4所示。

在这个流程图中，PCNN与STF挑选并增强待恢复图像退化点这一步，可以用细化的流程图，如图5所示。本文采取了两步走增强退化点，第一步用PCNN挑选退化点，送入STF中增强，接着对待增强图像提取边缘点，对第一步中选取的退化点进行有效的剔除，可以有效的保护好边缘不受处理，进而对新挑选出来的退化点进行重新送入STF处理，最后输出图像。

图4 PCNN-STF算法流程图

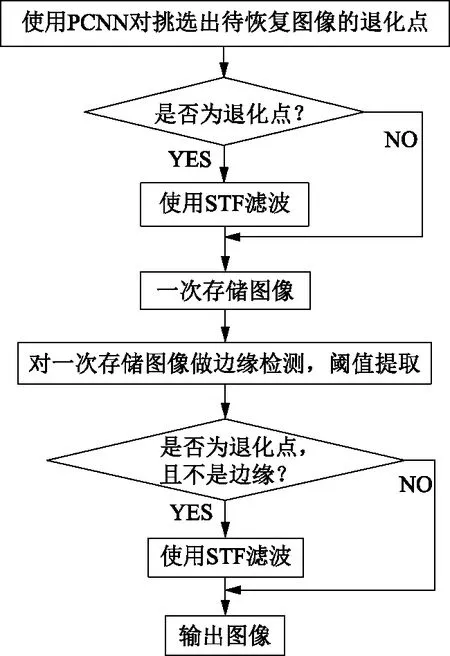
图5 边缘剔除算法流程图

4.2 算法检测原理

算法使用的检测算法是信息熵H和PSNR值，下面给出两种方法的计算公式：

(19)

(20)

(21)

式中，pi—图像中灰度值为i的像素所占的比例；l—灰度级，与图像的存储级别有关；Imax—输入图像最大灰度级。

4.3 实验环境及对比结果

为了验证PCNN-STF算法比传统PCNN算法的优越性，这里主要对比的算法主要是PCNN-中值和PCNN-平均值，实验采用了图1作为输入，实验的环境是MATLAB7.11，后期会将算法用OPENCV实现集成入相机处理算法中，实现算法的实时运行，进而可以测试算法的时效性，准确性。

图6—8分别给出了经过PCNN-STF，PCNN-中值，PCNN-平均值算法给出的输出效果图，表1给出了三种算法的熵和PSNR的对比值。

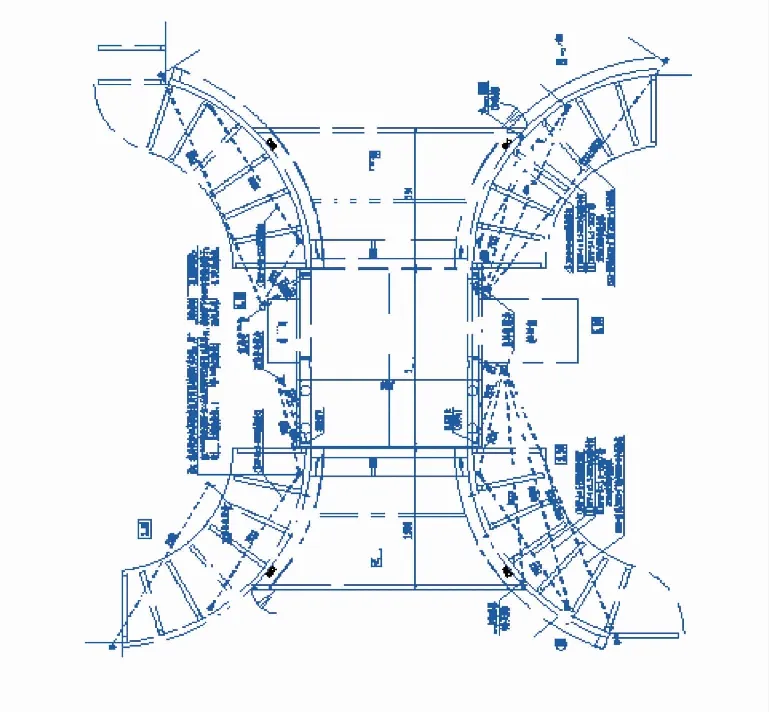
图6 PCNN-STF复原效果图

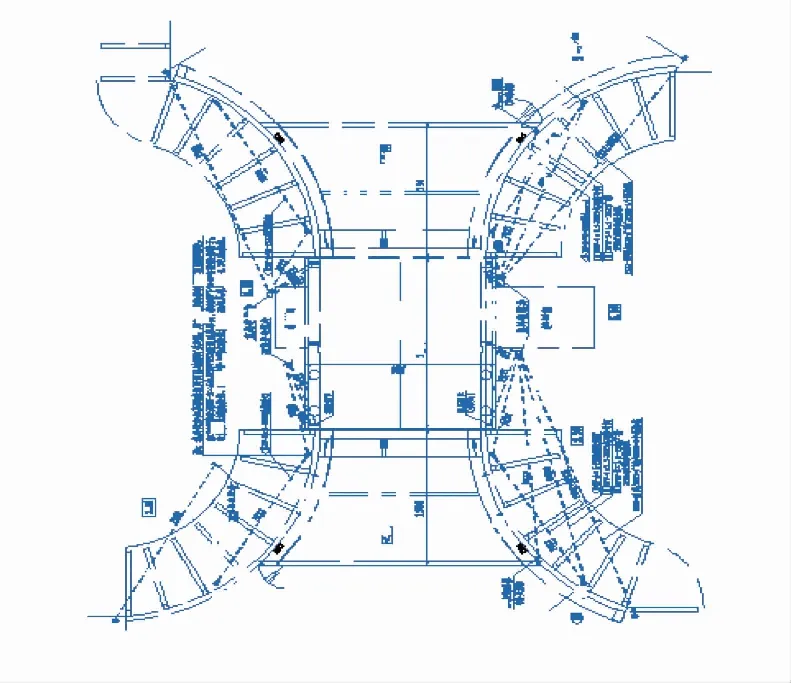
图7 PCNN-中值复原效果图

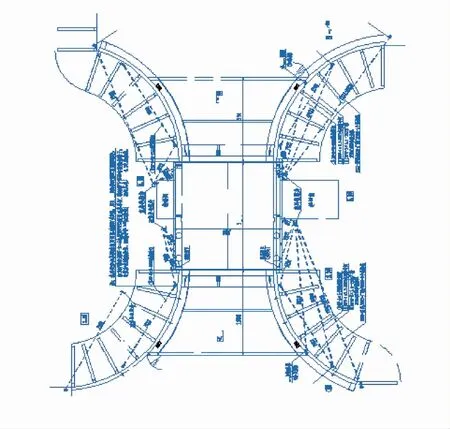
图8 PCNN-平均值复原效果图

本文选取的是10年前泵站站身的工程图纸，对比图6—8可以看出，PCNN-STF算法的直观效果最好，此外从表1可以看出PCNN-STF算法熵值较高，PSNR值较低，熵值反映了一幅图的细节，说明新算法保护细节的能力比较强，PSNR值往往不能真实反映图像给人的直观映像。

5 结语

针对图纸晒蓝后保存过程中，因时间过长导致图纸上的线条淡化模糊，本文对传统PCNN修复算法提出改进，提出了PCNN-STF算法，不仅有效的复原了图纸，并且在保护细节的能力上也有了不小的提升，不过对于图纸上一些尺寸数字并不能很好的修复，因为这些数字的信息丢失过大，修复难度过高，因此本文暂时无法进行修复。