数字滤波器相位的理解

陈国泰 张赛男 付 爽

(福建师范大学福清分校 a.无损检测技术福建省高校重点实验室；b.电子与信息工程学院；c.海洋研究院，福建 福清 350300)

在《数字信号处理》课程教学中，滤波器这一部分的内容很大程度上集中在幅频响应上，相频响应这一内容讲解得比较少。本文的目的是重新理解相位对滤波效果上的影响。

滤波器是一种最常见的信号处理形式，用来消除某些频率并且改进其他一些频率的幅值、相位或信号频谱某些部分的群延迟[1]。滤波器可分为模拟滤波器[2]和数字滤波器[3]316。模拟滤波器与后端的模数转换(ADC)采样率无关，可以滤除宽频带信号，适用于做抗混叠滤波器。模拟滤波器有有源和无源之分。

无源模拟滤波器主要由电阻、电感和电容构成，有源滤波器主要由运放、电阻和电容构成。无源滤波器结构相对简单，成本较低，有源滤波器虽然成本高，但滤波效果好，稳定度和精度较高。模拟滤波器的缺点是滤波器由元器件搭建，一旦搭建完成，很难修改滤波参数，并且阻带最小衰减很难达到-60dB[4]。

随着信息技术的发展，信号数字化在各领域得到广泛应用。数字滤波器也是常用的数字信号处理方式。数字滤波器的参数容易修改，阻带最小衰减很容易达到-60dB，精度和可靠性都很高。在线性系统中，数字滤波器在实际应用中由数字乘法器、加法器和延时单元构成。数字滤波器的缺点是受限于奈奎斯特采样定理，与前端的ADC采样率有关，所处理的信号频率宽带必须小于采样率的一半，否则会出现频率混叠。因此，在一些应用中，必须在ADC前端加上抗混叠的模拟滤波器以避免数字信号失真并导致系统的可靠性降低[4]。

在《数字信号处理》课程[5]中，尽管有提到相位问题，但相位在滤波中的作用并没有深入讲解。本文考虑在线性时不变系统中，关于数字滤波器相位的问题。

1 相位对波形的影响

在线性时不变系统中，满足Dirichlet条件的任何一个实信号可以用三角级数来表示[6]。基于奈奎斯特采样定理，这里假设考虑的实信号是平滑的，即实信号可以用有限个三角函数来表示。为了说明方便，用带初始相位的余弦函数(如来表示实信号。图1(a)是由在采样率为100下的函数曲线，即由频率为3和7的余弦波叠加而成。当频率为3的余弦波发生延迟，延迟的相位为 时，这时叠加的波形如图1(b)所示。虽然两个具有相同的频率成分，而且频率成分的幅度也相同，但波形发生了变化，这对依靠波形表征的信号，如语音、图像等而言，波形变化所表达的信息也发生了变化。当将用于表达图1波形的数据用于表达图像颜色时所表现的效果如图2所示，可以看到明显的不同，图中上方的短线为图2(a)和图2(b)之间较大区别的位置。因此，在图形处理中，相位会影响图形的表达效果。

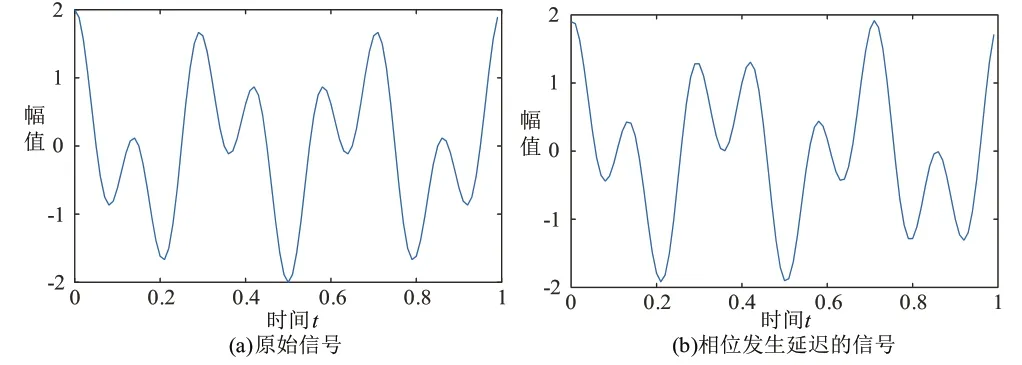
图1 由绘出的波形

图2 由数值作为颜色数据所绘出的图形

2 FIR数字滤波器及其相位

在线性时不变的离散系统中，有限冲击响应是在单位脉冲输入下系统输出的是有限长度的序列。当有限冲击响应序列是对称的时候，对应的数字滤波器具有线性相位特性[3]467。

假设有限冲击响应实序列为h(n)(n=0,…,N-1)，则该序列的傅里叶变换为

当序列h(n)为偶对称时，即h(n)= h(N-1-n)，有

故得

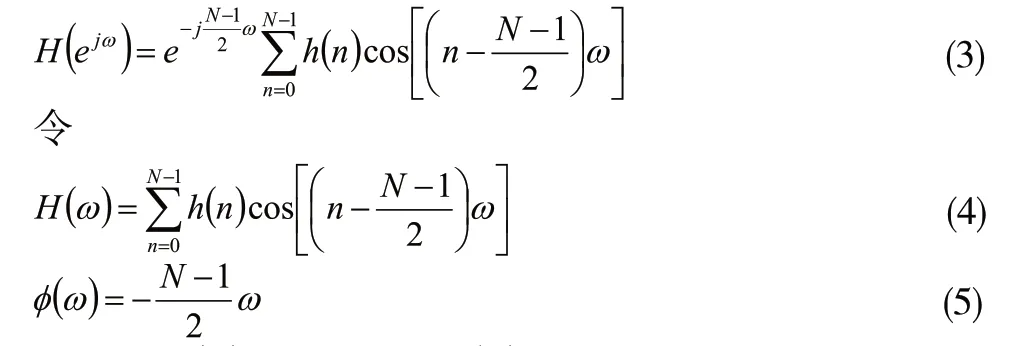
当序列h(n)为偶对称时，即h(n)=-h(N-1-n)，同理可得

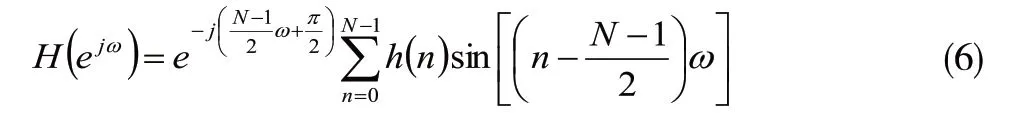
根据序列奇偶对称性以及奇偶长度的不同，共有四种情况，每种情况通过分析在为0，π和2π处的函数值和对称性，可以得到式(3)和式(6)在什么时候适合设计哪种FIR数字滤波器，如表1所示。

表1 不同对称性和长度下所适合设计的FIR数字滤波器

根据上面的分析，冲击响应为对称序列的数字滤波器的相位是线性的，除了第一类和第二类线性相位的差别外，同一类之间有什么差别呢？这里结合例子来展示其差别。

从表1可知，四种情况都可以用于设计带通滤波器。考虑一个信号为滤波器采用矩形窗函数，滤波器的阶数分别为12和13，采样频率为100Hz，截止频率分别为6Hz和14Hz，在Matlab[7]环境下利用filter函数实现滤波，滤波后去除结果中的前6个数据，这时由于滤波器作为因果滤波器事先做了时间上的平移。各种不同情况下的带通滤波器的滤波效果，如图3所示。

图3 各种不同情况下带通滤波器滤波的效果

从滤波的效果看，第一类线性相位下的两种滤波器的滤波输出波形很相似，如图3(b)所示，同样，第二类线性相位的两种滤波器产生的滤波结果也很相似，如图3(c)所示。图3(d)是用第三种带通滤波器对原始信号滤波的结果以及用第一种滤波器对相移90°后的原始信号(即滤波的结果，图中结果表明了第三种滤波器对原始信号滤波相当于对于相移90°后的原始信号采用第一种滤波器进行滤波。图3(d)中在t=0s附近两条曲线不吻合的原因是在filter函数中初值为0，需要经历12离散点(即滤波器长度减去1)后，滤波结果即非常吻合。实际上，四个滤波器在频率幅度上是存在差别的，如图4所示，偶对称的偶数阶滤波器在低通部分性能略差，通带内也略有差别。总体上，在通带内，四种滤波器的性能比较接近，在高频方面有一些差别。当信号的频率成分丰富时，滤波后的波形会存在一些差异。

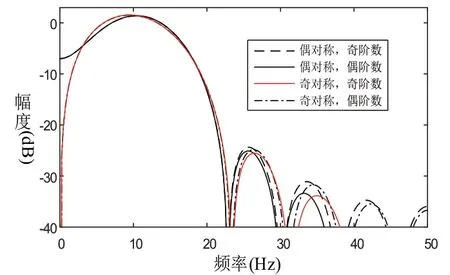
图4 四种FIR带通滤波器的幅频响应

图3 (b)中第二种滤波器表现了其滤波结果的相位产生超前，这是因为实际滤波后的信号需要平移(12-1)/2=5.5点，但图中实际向左平移了6个点，因此，相位超前了1/(2Fs)。图3(c)中的第四种滤波器也是同样的情况。这意味着当滤波器的阶数为偶数时，滤波结果总会产生这样的相位超前或延迟。

图3(a)显示了原始信号经过第一种带通滤波器滤波，波峰和波谷的数量有减少，高频的信息得到一定的去除，另外，也可以看出波峰值和波谷值的绝对值之间的差值也有所变小，这表明了低频成分也得到了一定的去除。

从滤波器的结构来看，第二种滤波器序列是偶数阶的偶对称，滤波时相当于是对对称位置的数据求和(或求平均)后再乘以权值，这种求和实际上是平滑操作，即滤除高频信息的操作。第四种滤波器序列是偶数阶的奇对称，滤波时类似于对对称位置的数据求微分后乘以权值，直流成分在这种滤波器下是会被滤除的，微分在图像处理中用于边缘检测[8]，因此，可以保留高频信息。第三种滤波器序列是奇数阶的奇对称序列，序列的中间位置元素为0，同样具有滤除直流和低频信息的效果。虽然第三种滤波器具有第四种滤波器的那种类似微分运算的操作，但由于滤波器序列的中间位置元素为0，造成这种类似微分操作是在更宽的范围内进行，而且中间的元素没有参与运算，因此，操作所得的信息是中低频信息，高频的信息被滤除。这就是第三种情况不能用于设计低通和高通的原因。在第一种滤波器设计中，滤波器序列是奇数阶的偶对称，中心位置的值占很大比重。滤波操作可以看成相关运算，在以正弦波(或余弦波)构成的信号下，显然，低通滤波器的序列应该表现出相对比较平滑，高通的滤波器序列应该波动比较剧烈，带通和带阻滤波器也可以类推。第一种滤波器可以实现低通、高通、带通、带阻等四种滤波器。

3 IIR数字滤波器及其相位

汪芙平等[9]证明，IIR数字滤波器不具备实现线性相位特性，但在实际应用中，相位非线性变化不大的IIR数字滤波器可以近似为具有线性相位的，或者借助一个全通网络来进行相位矫正[3]320。

N阶IIR数字滤波器通常用z-变换函数表示为

其中，b(n)用于控制零点在z平面内的位置或偏离单位圆的程度，a(n)用于控制极点在z平面内的位置。稳定的系统要求极点必须在单位圆内。靠近单位圆的极点容易因量化误差或其他误差导致极点偏离到单位圆上或单位圆外，导致系统失效[3]618。

IIR数字滤波器的设计可以利用模拟滤波器的设计方法通过脉冲响应不变法和双线性变换法等进行[3]386-390。脉冲响应不变法是使数字滤波器在时域上模仿模拟滤波器，其缺点是容易造成混叠失真。双线性变换法是从频率出发，使数字滤波器的频率响应与模拟滤波器的频率响应相似的一种变换法。这种方法适用具备封闭式的公式进行计算。

Matlab中的FDAtool对话框界面可以快速设计低通、高通、带通、带阻等滤波器，包括FIR滤波器和IIR滤波器。这里将设计两个IIR滤波器，以显示IIR具有非线性相位。

设计的数字滤波器仍然是带通滤波器，采样频率为100Hz，截止频率分别为6Hz和14Hz，IIR滤波器的阶数为4，在FDAtool中Design Method选项中，IIR分别选择Butterworth和Chebyshev Type I，这两个滤波器的幅频响应和相频响应如图5所示。对比图4，IIR滤波器在阶数较低的情况下，幅频响应的性能比FIR滤波器好，IIR滤波器的相位延迟不满足线性变化，如图5(b)所示。

图5 中的幅频特性和相频特性结果是根据式(7)得到的，其中FDAtool中导出设计好的数据SOS和G，通过函数sos2tf得到a(n)和b(n)，再计算由此求出幅频特性和相频特性，相频特性先通过angle函数再用unwrap函数得到平滑曲线。

考虑一个频率为10Hz的余弦波 分别输入到这两个滤波器中，滤波后的结果如图5所示。从相频特性中得到10Hz在Butterworth中为-0.248 332 106 920 221，在Chebyshev Type I滤波器中的相位为-0.176 160 430 570 338，将相位延迟代入余弦波中，即cos(2π×10×t-0.248 332 106 920 221)，从图6可以看到滤波后的信号和加入相位延迟的信号是吻合的。由于Chebyshev Type I滤波器在通带内有波纹，因此，图6(b)的波形幅度有所减少。

图6 表明，通过相频特性可以得到每个频率经过滤波后产生相位延迟或相位超期的相位值，有助于更好地理解滤波后波形变化。

4 相位延迟和群延时

在前面的例子中，图6考虑的是单个频率的信号作为滤波时的输入信号，相位延迟就是指滤波后信号与输入信号的相位偏移[10]。将滤波器的傅里叶变换记为那么相位延迟一般考虑的是时间延迟[11]。

比较容易理解的例子就是一个正弦波的峰值进入滤波器(或系统)到滤波器与滤波器输出该峰值所对应峰值之间的时间差。相位延迟只关心单个频率的情况。

当输入信号包含多个频率时，这时考虑的是群延迟[12]，群延迟的表达式如式(9)所示。

群延迟考虑的是式(9)是否为一常数，以表示包络是否完整包含相关信息。当群延迟为一常数时，滤波器(或系统)具备线性相位特性，如具有线性相位的有限冲击响应滤波器。在第一类线性相位中，每个频率的相位延迟时间是相同的，只是波形全体提前到达或是延迟达到，整体的包络波形保持不变。在第二类线性相位的情况下，所有频率波形都同时达到，但是达到时都已经发生相同的相位偏移，因此，包络的形状可能会发生变化，由于相位偏移是已知的，包络的信息不会出现失真。当群延迟不是一个常数时，若 不包含常数项，那么每个频率的波形到达的时间不一致，假设只有一个频率波形延迟达到，其他频率仍然在原有的包络中，而这个延迟的频率所对应的波形将有一部分在当前包络中，另一部分将跨越到下一个包络中，这种情况造成符号干扰。在通信系统中，群延迟不是常数时会引起符号间干扰和传输波形失真[14]。当 包含常数项时，如同前面所说，每个频率的波形到达时都已经发生了相同的相位偏差。

数字滤波器的设计是要使滤波器尽量具备线性相位特性，或者保证通带内的频率具备线性相位特性，这样滤波后信号能够较好地保留相应的信息，使表达效果没有明显的失真。图5(b)中由Butterworth设计而来的IIR数字滤波器在通带内群延迟近似为常数。

群延迟的计算可以通过计算相邻频率之间的相位微分得到。

5 结论

由于对称序列的有限冲击响应滤波器具有线性相位特性，而无限冲击响应滤波器不具备线性相位特性，因此，教材没有深入讲解相位问题。本文通过例子来显示相位对信号在信息表达上的影响，分析了有限冲击响应带通滤波器在四种设计方案下的相位差异，再通过单频波经过无限冲击响应带通滤波器来分析信号滤波前后的相频特性变化，最后谈到相位延迟和群延迟。这些内容有助于在学习数字信号处理课程时对相位有更深刻的理解。