极限四则运算法则在抽象函数敛散性判定方面的应用

邵伟如 北京交通运输职业学院基础部

1 引言

在使用四则运算法则计算极限时需要注意其使用前提,即参与运算的各部分函数极限必须存在，否则会导致计算的错误.但是这一前提限制了函数极限计算的适用范围，尤其在讨论抽象函数的敛散性时，往往不能像具体函数那样明确知道函数本身的极限是否存在，判定难度很大。

2 理论基础准备

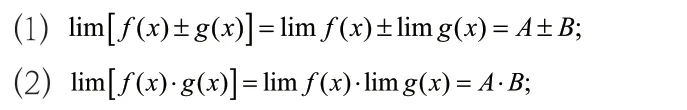
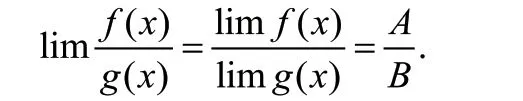
当定理1 中进行极限计算的两个函数极限不存在时（包括极限均为无穷大的情况），四则运算法则是不适用的。

3 极限四则运算法则在抽象函数敛散性判定方面的应用

在这一小节对四则运算法则的适用范围做了推广,将四则运算法则中要求的参与运算的各部分函数极限必须都存在这一条件，推广至只需在确定部分函数极限存在的情况下就可以对最终函数的敛散性做出判断。

定理2 也表明，当计算两个或有限个函数和差的极限时，当一部分极限存在，那么也可以使用四则运算法则，此时极限的情况取决于的情况。

解：

定理3 也表明，当计算两个或有限个函数乘积的极限时，当一部分极限存在且不为零时，那么也可以使用四则运算法则，此时极限的情况取决于的情况；若存在极限的部分极限为零时，则最终函数极限是不能判定是否存在的，需要根据具体的情况去处理。

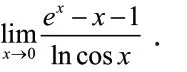
解

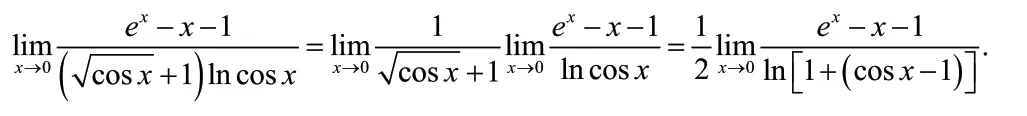
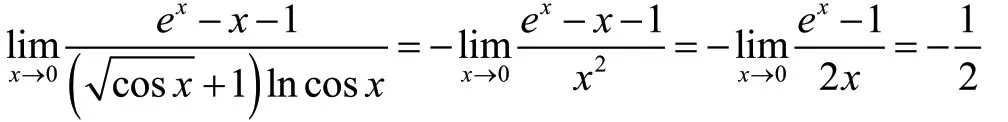
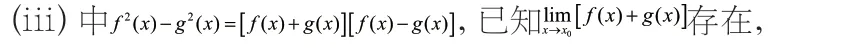
4 结论

在高等数学的学习过程中，会涉及到很多公式及定理，在应用这些公式、定理之前，一定要注意检查是否满足使用条件。比如，极限运算的四则运算法则、复合函数的极限运算法则、洛必达法则等等，都是有使用前提的，不能盲目地去套用公式、定理。而数学学习的一个很重要的方面就是锻炼这种逻辑的严密性。