身体活动、静坐行为的时间分布与肥胖的关系
2020-06-23那晓娜陈阳阳王东平王浩杰马晓川王培玉刘爱萍
那晓娜,朱 珠,陈阳阳,王东平,王浩杰,宋 阳,马晓川,王培玉,刘爱萍△
(1. 北京大学公共卫生学院社会医学与健康教育系,北京 100191; 2. 乌海市疾病预防控制中心,内蒙古自治区乌海 016000)
肥胖是影响我国居民健康的重要公共卫生问题,有研究证实,肥胖是高血压、糖尿病、消化系统疾病、肿瘤等多种慢性疾病的重要危险因素[1]。一项全球研究显示,2014年我国男性、女性轻度肥胖人数均已超越美国,居世界首位,而男性、女性重度肥胖人数均居世界第二,仅次于美国[2]。既往研究表明,肥胖指标[如体重指数(body mass index, BMI)、腰围身高比(waist to height ratio, WHtR)]与身体活动时间、静坐时间均有关[3-5]。目前多数研究仅单独探讨了身体活动(physical activity, PA)或静坐行为(sedentary behavior, SB)时间与健康结局的关系[6-7],然而,每日时间是固定的,PA、SB的时间相互影响,这种数据属于成分数据[8]。
目前,国际上已经逐渐认识到运用传统统计学方法分析PA、SB时间数据存在的问题,2014年有学者提出,使用传统的统计学方法分析时间数据将得出错误的结论,呼吁使用成分数据分析方法[9]。随后,国际上出现了一系列相关研究和政策指南[8, 10],例如,加拿大运动生理协会组织各领域的专家及代表通过系统综述以及成分数据分析方法,分析儿童和青少年的每日PA、SB、睡眠时间的分布与健康的关系,制定了《加拿大5~17岁儿童青少年24小时身体活动、静坐、睡眠的时间分配指南》[11]。我国亟须将成分数据分析方法运用于运动指南的制定中,本研究将采用成分分析方法探究居民PA、SB时间的分布与肥胖的关系,以期为我国相关指南的制定提供科学依据。
1 资料与方法
1.1 研究对象
研究对象为乌海市18~79岁常住居民(在过去12个月中,在乌海市累计居住6个月及以上者)。本研究获得北京大学生物医学伦理委员会批准(IRB00001052-16022), 研究对象参加调查前签署知情同意书。
1.2 研究方法
1.2.1抽样方法 为保证样本年龄、职业、地理位置的代表性以及课题的可行性,采用多阶段整群随机抽样方法,从乌海市三个核心行政区(海勃湾区、海南区、乌达区)共20个街道抽取职业与非职业人群。职业人群以六大行业(建筑业、制造业、批发零售业、餐饮住宿、社会服务、其他行业)为框架,根据乌海市行业构成,选取105家拟调查单位,以男性年龄<55岁,女性<50岁者作为拟调查对象,根据工资号进行系统抽样选取最终研究对象。非职业人群则从所有街道中随机选取2个街道居委会,以男性≥55岁,女性≥50岁且已退休者作为拟调查对象,每个居委会抽取100户居民,按照Kish表法从每户中选择1名符合条件的成年常住居民作为研究对象。排除标准:严重认知困难或孕妇。
1.2.2问卷调查 采用自行设计的问卷,由经过统一培训并考核合格的调查员调查研究对象的社会人口学特征、吸烟史、饮酒史、饮食摄入情况、PA和SB时间等。PA调查参考国际身体活动问卷(International Physical Activity Questionnaire,IPAQ)长卷[12],获得研究对象过去1个月中,各种强度的PA频率、次数和时间,以及平均每天SB时间。IPAQ长卷是目前公认有效、且在国际上较广泛使用的成人PA水平测量问卷之一[13],在中国人群中的效度与信度较高[14-15]。饮食摄入调查参考简化膳食频率调查问卷,结合当地饮食习惯,调查研究对象过去1个月饮食摄入的频率、次数和质量,此问卷在中国人饮食调查中具有较高的信度和效度且简便易用,适合大规模的流行病学调查[16]。
1.2.3体格测量 体格检查均在二级及以上医院进行,由专业医师操作完成。体检人员应用校正后的仪器,按照标准的操作方法,测量研究对象在清晨空腹、直立状态下的身高、体质量、腰围,测量两次数据记录平均值。身高测量方法为:用标准测量仪器测量研究对象头顶点至地面的垂直距离(cm),精确至0.1 cm;体质量的测量方法为:采用标准体重计测量研究对象仅身着贴身衣物时的体质量(kg),精确至0.1 kg;腰围的测量方法为:受试者直立,仅穿贴身衣物,两脚分开约30 cm,测量正常呼气末肋弓下缘与骼骨嵴连线中点的水平周径(cm),准确至1 cm。
1.3 诊断标准及相关定义
PA、SB的时间:根据IPAQ工作组建议的PA强度判定标准[13],PA分为高、中、低强度,因高、中强度PA有明显促进健康的作用[17],故将高、中强度PA合并,称为中高强度身体活动(moderate-to-vigorous physical activity, MVPA),不满足MVPA标准的则定义为低强度身体活动(low-intensity physical activity, LIPA)。将PA、SB的时间单位统一为分钟。
肥胖指标:BMI=体质量(kg)/身高(m)2;WHtR=腰围(cm)/身高(cm)。
1.4 统计学分析
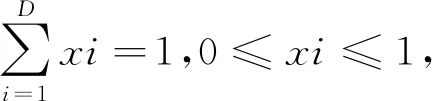
每日时间属于成分数据,而在实际调查中,可能出现未调查完整成分数据的情况,仅有其中一部分数据可运用“闭合法”或者“填充法”。“闭合”即将获得的这部分数据“闭合”为合理的固定值(实际上,由于成分以相对比例表示,所以无论“闭合”为何固定值,对最终分析结果都无影响)[20]。已有研究通过“闭合”的方法探究每日苏醒时间分布与健康结果之间的关系[21]。“填充”即用成分总和减去获得成分的总和,得到未调查部分的成分数据,再将所有成分数据纳入分析,这两种方法所得的分析结果是几乎一致的[20]。另外,目前睡眠与肥胖之间的关系尚无定论,过多或者过少的睡眠都将导致肥胖,因此此次研究仅探讨苏醒时活动的时间分布与肥胖之间的关系,采用“闭合法”,将每日苏醒时间“闭合”为16 h(研究对象平均睡眠时间为8 h)。采用R 3.6.2统计软件中的compositions包对成分数据进行统计描述与分析处理,以P<0.05(双侧)为差异有统计学意义。通过compositions包的“clo”函数“闭合”为16 h(960 min),通过“ilr”函数计算两种成分的等距对数比[22]。
括号内为T值,调整后的R2为0.2240,F值为7.35,并在5%显著水平下通过检验。由结果可知资本产出弹性α=0.6454,劳动产出弹性为0.3546。因为二阶差分后,弱化了常数项,所以常数项并不显著。将α值代入(3)式,即可得全要素生产率的增长率,结果见表2。
通过成分均数以及方差矩阵描述PA、SB的分布特征,其中,成分均数描述集中趋势,并比较与传统算术均数的差异;采用成分等距对数比方差矩阵,描述成分数据的离散程度,矩阵中的数值表示成分之间的关联程度。采用成分线性回归,分析MVPA、LIPA、SB时间占比与BMI、WHtR的关系。WHtR经负自然对数变换(-lnWHtR)后,符合正态分布再进行分析。成分回归的拟合方式为将各项PA、SB的时间作为整体,计算活动之间的等距对数比,再采用传统的线性回归模型进行拟合。成分回归的结果可解释为:某项活动时间占比(而非绝对时间)与肥胖的关系。也采用传统线性回归方法,将PA、SB纳入回归模型,比较传统回归模型与成分回归模型之间的差异。两种模型调整年龄,性别,学历,家庭年收入,吸烟史,饮酒史,谷薯类、蔬菜水果、肉类摄入总量,高血压、糖尿病、血脂异常的控制情况。
根据拟合的成分回归模型,计算时间重新分配后BMI、-lnWHtR的预测值变化,比较MVPA、LIPA、SB时间对肥胖的影响程度。采用既往研究中的重新分配方法[23],即以10 min为单位,将某种活动的10 min分配给另一种活动,而其他活动时间不变,以保持总时间(960 min)不变,计算重新分配时间后的时间分布与原始时间分布的BMI、-lnWHtR的差值。
2 结果
2.1 基本情况
研究对象年龄、性别、文化程度、家庭年收入、MVPA和SB的时间、BMI、WHtR信息完整的共5 121人,平均年龄(43.79±12.57)岁,其中男性1 924人(37.57%),女性3 197人(62.43%);职业人群3 773人(73.68%),非职业人群1 348人(26.32%);文化程度大专以下3 019人(58.95%),大专及以上2 102人(41.05%);家庭年收入3万元以下2 053人(40.09%),3万~8万元2 301人(44.93%), 8万及以上767人(14.98%);有吸烟史者1 451人(28.33%),有饮酒史者2 320人(45.30%)。
2.2 PA、SB的时间分布
不同性别的PA、SB时间分布相似,而职业与非职业人群分布有所差异,因此按照职业与非职业人群分类描述分析。比较传统算术均数与成分均数描述PA、SB时间的集中趋势结果显示,两种方法对集中趋势的描述存在差异,与成分均数相比,两类人群中算术均数对不同活动时间有一定程度的低估或高估(表1)。
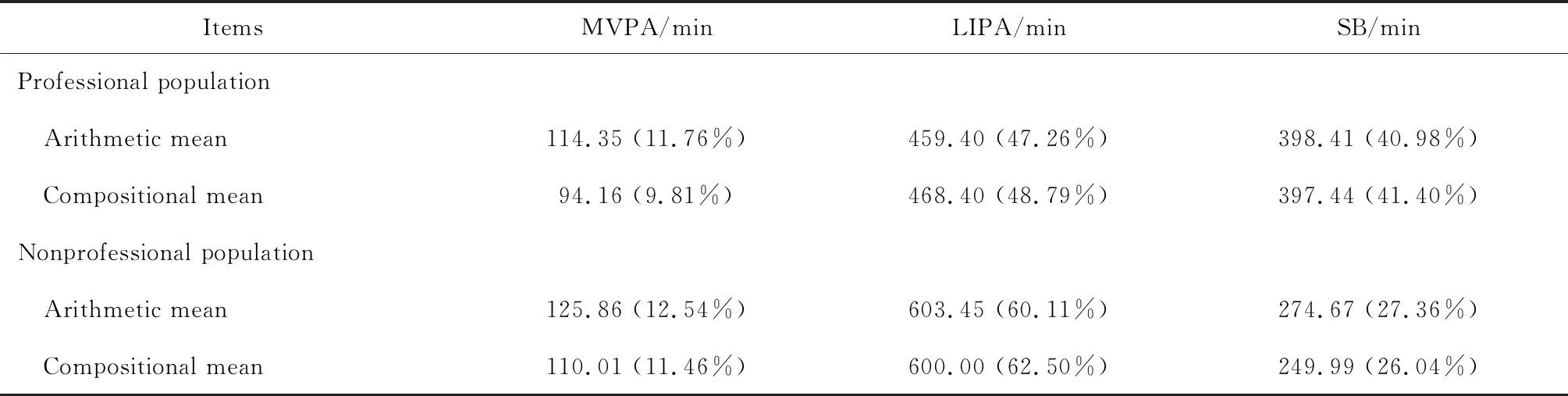
表1 身体活动、静坐时间的算术均数与成分均数比较
MVPA, moderate-to-vigorous physical activity; LIPA, low-intensity of physical activity; SB, sedentary behavior. Results of arithmetic mean expressed in proportion of actual total time, compositional mean expressed in proportion of 960 minutes.
运用成分方差矩阵描述不同人群活动时间的离散程度(表2),矩阵中的数值为两项成分等距对数比的方差,越接近0说明两项活动之间的关联程度越大。本研究结果显示,职业与非职业人群中,MVPA与SB等距对数比的方差最小,说明这两项活动的关联程度较强,而与其他活动之间的关联程度相对较低。进行分析时若忽略PA、SB的本质关系,采用传统统计学方法将PA、SB作为独立的变量纳入分析,可能出现伪相关的结果。
2.3 PA、SB的时间分布与BMI、-lnWHtR的关系
成分回归模型结果显示(表3),控制潜在混杂因素后,职业人群(BMI:P<0.001,adjustedR2=0.14;-lnWHtR:P<0.001,adjustedR2=0.16)与非职业人群(BMI:P<0.001,adjustedR2=0.16;-lnWHtR:P<0.001,adjustedR2=0.17)PA、SB的时间分布与BMI、-lnWHtR的关系均有统计学意义。职业人群中,MVPA时间占比与-lnWHtR呈负相关(β=-0.008,P=0.022),静坐时间占比与BMI、-lnWHtR呈正相关(β=0.117,P=0.003;β=0.007,P=0.005)。非职业人群中,MVPA时间占比与BMI呈负相关(β=-0.079,P=0.041),SB时间占比与BMI、-lnWHtR的关系无统计学意义。职业与非职业人群中,LIPA时间占比与BMI、-lnWHtR的关系均无统计学意义。
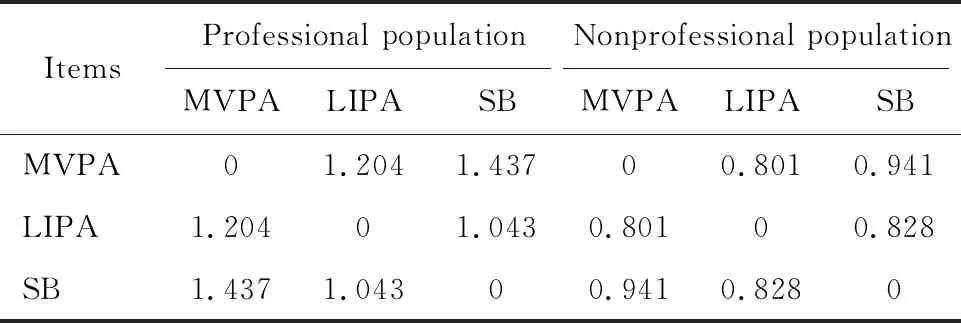
表2 身体活动、静坐时间的成分方差矩阵
Abbreviations as in Table 1.

表3 肥胖与身体活动、静坐的时间分布的成分线性回归分析
BMI, body mass index; WHtR, waist to height ratio; other abbreviations as in Table 1. Adjusted for age, gender, education, annual household income, smoking history, alcohol history, daily total intake of cereals, tubers, vegetables, fruit, meat, controlling of hypertension, diabetes, dyslipidemia in all models.
传统线性回归结果显示,调整潜在混杂因素后,MVPA、LIPA、SB占比与BMI、-lnWHtR的线性关系无统计学意义。
2.4 时间重新分配BMI、WHtR预测值变化
职业人群中,将10 min LIPA或SB分配给MVPA后,BMI(-0.464,-0.462)和-lnWHtR(-0.019,-0.018)将减小;将10 min MVPA分配给LIPA后,BMI(0.446)和-lnWHtR(0.017)将增大;10 min SB分配给LIPA时,BMI(-0.456)和-lnWHtR(-0.015)将减小;10 min MVPA、LIPA分配给SB时,BMI(0.445,0.455)和-lnWHtR(0.017,0.017)将增大(表4)。
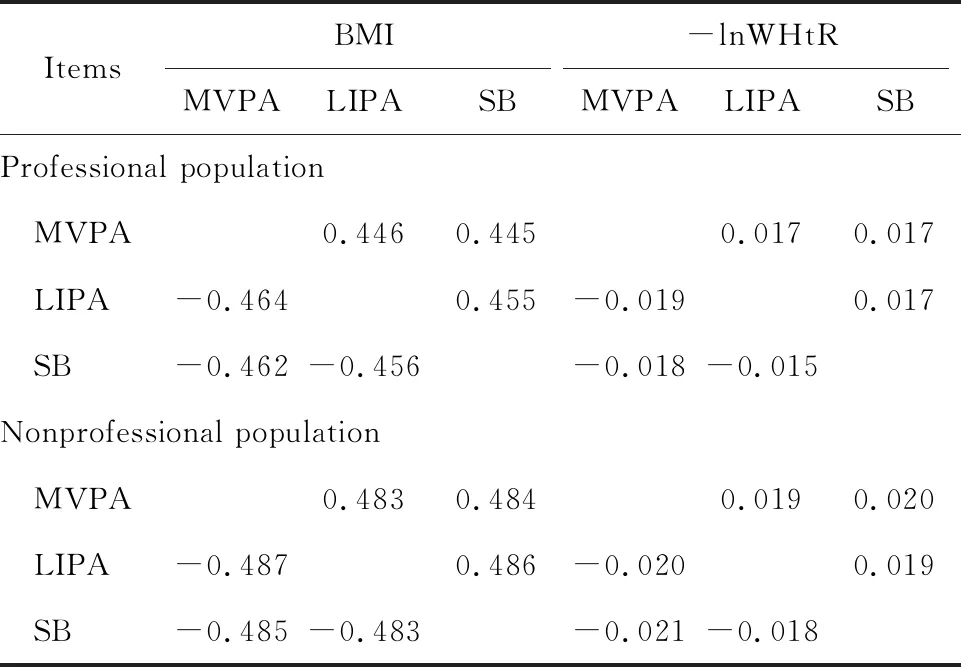
表4 身体活动、静坐时间重新分配的BMI、WHtR预测值变化
Abbreviations as in Table 1 and 2. Adjusted for age, gender, education, annual household income, smoking history, alcohol history, daily total intake of cereals, tubers, vegetables, fruit, meat, controlling of hypertension, diabetes, dyslipidemia in all models.
此外,BMI、-lnWHtR的预测值变化情况与传统线性回归不同,呈非对称性,与MVPA分配给其他活动时相比,其他活动时间分配给MVPA时的BMI和-lnWHtR变化较大。
3 讨论
目前探究MVPA、SB对健康影响的研究,常采用传统的统计学方法,未考虑到每日时间的“定和约束”,改变其中一项活动的时间必定会影响其他活动,最终直接或者间接影响健康[8]。既往研究也显示,运用传统的统计学方法将出现伪相关和多重共线性问题[10]。本研究结果也表明,PA、SB的时间是相互联系的,与既往采用成分数据分析的研究结果类似[23]。目前成分数据分析方法已经应用于多个领域,可以较好地在方法学上解决成分数据存在的问题。通过将数据进行合理转化,为成分数据的分析提供了统计学上的合理性,可以避免直接运用传统统计学方法分析此类数据出现的问题[18]。
本研究考虑到每日时间的“定和性质”,运用了成分数据等距对数比转换的方法,综合探究PA、SB的时间分布与BMI、-lnWHtR的关系,结果显示,MVPA时间占比与BMI、-lnWHtR呈负相关,SB占比与BMI、-lnWHtR呈正相关,与以往研究结果相一致[21],说明提高MVPA时间、降低SB,可能减小BMI、WHtR,降低全身性肥胖或中心性肥胖的风险。LIPA时间占比与BMI、-lnWHtR的关系无统计学意义,与既往采用成分分析方法的类似研究结果一致[21],但与传统统计方法的研究结果有所不同[7],可能是由于研究方法以及样本的代表性不同,因此,关于LIPA时间与肥胖的关系需要运用成分数据分析方法对有代表性人群行进一步论证。职业与非职业人群中,活动时间分布与BMI、WHtR的关联有所不同,可能是由于职业与非职业人群的年龄差异,导致PA对于职业人群肥胖风险的降低更明显。
时间重新分配后结果显示,LIPA或SB的时间分配给MVPA后,BMI和WHtR将减小;MVPA分配给LIPA后,两者将增大;SB分配给LIPA时两者将减小;MVPA、LIPA分配给SB时,两者将增大。与MVPA分配给其他活动时相比,其他活动时间分配给MVPA时BMI和-lnWHtR的变化较大,进一步提示MVPA可能对BMI和WHtR具有重要影响,应尽量将其他活动转变为MVPA,以维持合适的BMI和WHtR,降低肥胖以及中心性肥胖的风险。对于一些高强度体力劳动者,虽然在工作之余增加MVPA的可能性较小,但是可以尽量避免静坐,将静坐时间分配给其他类型的活动,就有减少肥胖风险的可能。
综上,本研究结果提示,在运动指南制定以及健康管理的实际工作中,应考虑每日时间有限这一事实,采用成分数据分析方法,综合考虑PA、SB的时间分布对健康的影响,而非简单地提高MVPA、减少SB的绝对时间,才能取得长远的健康效果。针对不同群体或者个体,应从时间分配干预的角度,结合可靠的前瞻性研究,提出具体的个性化方案以及健康指南,以尽量获得最高的健康效益。
本研究存在一定的局限性,首先本研究采用横断面调查,无法进行因果推断,需要今后开展随访研究进一步探讨;其次,时间信息通过问卷调查获得,存在一定的回忆偏倚,在今后的研究中可以运用可穿戴设备等更准确的方法获得更客观的时间信息;最后,本研究没有考虑睡眠时间与肥胖的关系,今后应探索成分数据分析方法在PA、SB、睡眠时间方面的应用,以得到更为可靠的结论,为我国运动指南制定以及健康管理实践提供参考。
