一种相关干涉仪与MUSIC算法相结合的改进测向算法

李彦龙，杨博盛

（中国人民解放军91404部队，河北秦皇岛066000）

0 引言

信号的波达方向（DOA）估计是阵列信号处理领域的一个非常重要的研究内容。其主要目的是通过提取空间中按一定方式排列天线阵列所接收信号的有用特征，用来估计信号的空域方位参数，因此国内外学者提出了一系列的DOA估计新算法。其中干涉仪测向技术以方法简单、速度快、技术成熟等优点而被广泛应用于各种领域。在常用的干涉仪测向方法中，相位干涉仪[1-2]测向方法存在相位模糊、受硬件通道不一致性影响较大等问题，性能不佳；相关干涉仪[3]测向方法是利用实际接收信号的相位差信息与样本库的数据作相关处理进行测向，算法运算简单，但测向精度及角度分辨力较差，且与样本库的质量具有很大的关系；基于子空间分解的多重信号分类（MUSIC）算法[4]是阵列信号处理学科发展的主要方向，该技术可以大大改善在系统处理带宽内空间信号的角度估计精度、角度分辨力及其它相关参数估计精度，因而在雷达、通信、声纳等众多领域有极为广阔的应用前景，但其运算复杂，实时性无法满足工程应用。

对于反辐射导引头[5]来说，导弹本身的超高速飞行，为满足打击精准率，其测向更新率需要达到几十甚至上百赫兹。MUSIC算法运算复杂，实时性较差，在反辐射导弹上的应用受到一定的限制。MUSIC算法中角度搜索占用了其大部分的时间，若给其一个大致范围内的引导角，则其计算量将大为减少，因而本文提出利用相关干涉仪算法大致计算出辐射源的位置，进而以此作为引导角在一定范围内进行MUSIC测向，该方法能够有效地提高测向更新率，满足反辐射导引头实时性要求。

1 算法原理

1.1 相关干涉仪

相关干涉仪测向的基本原理是对系统测量的相位差和系统原始相位差样本进行相关处理，计算出相关系数，相关系数的最大值对应的角度即为目标信号的来波方向角。这里以5元均匀圆阵为例，说明相关干涉仪测向原理

相关干涉仪测向需要两步：

1）建立相位差库

在给定频率范围与给定方位角范围内，分别等间距的选取若干方向(θ,φ)和频率f对任意一组入射角(θi,φi)和频率fi，可实际测量得到多个天线对的相位差。不同方位和不同工作频率下的相位差，可构造成一张二维表。

2）相关运算

解决相关运算主值区间边界处的相位跳变问题，同时为了减小相关运算的运算量和存储量，采用了基于三角函数的改进代价函数进行相关运算，该方法的表达式为：

式中，βm为测量的相位差，αm(θ,φ)为在(θ,φ)方向上的基于参考阵元的原始相位差样本，g(θ,φ)为相关运算产生的代价函数。当代价函数取得最大值时，相关系数最大，因此搜索g(θ,φ)最大值得到的角度即为目标信号的来波方向角。

1.2 MUSIC算法

MUSIC算法主要过程是对接收信号的协方差矩阵进行特征值分解，得到噪声子空间和信号子空间，然后利用这两个子空间的正交性，通过谱峰搜索寻找极值点进行DOA估计。

设天线阵列由M个天线阵元组成，后面接有M个接收通道，N(N＜M)个远场、窄带、独立的信号入射到天线阵列上，则在瞬时时刻t，第m个阵元输出信号为：

式中，X(t)和N(t)分别是M×1维天线阵列接收的信号矢量和噪声矢量；S(t)是N×1维信号矢量；A是M×N维的阵列流形矩阵。

阵列流形矩阵A由时延τ表达式确定，不同的阵列结构有不同的时延表达式。由于空间天线阵元位置不同，导致接收信号会产生波程差，从而产生时延τ。现推导空间中任意两个阵元之间的时延τ，天线阵元位置如图1所示，均匀分布在半径为R的圆阵上，以其中某一天线阵元为例，坐标为(x,y,z)。→SO表征入射信号，分别定义θ和φ为入射信号的方位角和仰角，对信号进行DOA估计实质就是对这两个角度进行估计。

图1 天线阵排列图

根据几何关系可以推得两阵元之间的时延为：

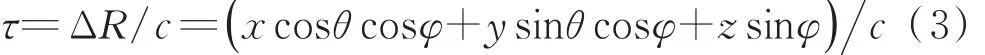
天线阵列接收信号的协方差矩阵：

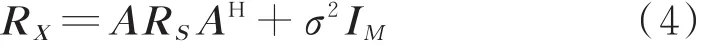
对R X进行特征值分解：

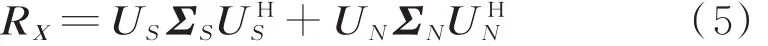
ΣS和ΣN是分别由大特征值λ1,λ2,…,λN和小特征值λN+1,λN+2,…,λM构成的对角阵。由N个大的特征值λ1,λ2,…,λN对应的特征向量构成信号子空间U S=[u1,u2,…,u N]， 由M-N个 小 特 征 值λN+1,λN+2,…,λM对应的特征向量构成噪声子空间U N=[u N+1,…,u M]。

根据导向矢量与噪声子空间正交，又由于导向矢量和信号子空间张成的空间是同一个空间，则可以证明噪声子空间和信号子空间是正交的。MUSIC算法的本质就是噪声子空间与信号子空间的正交性。通过搜索UHN a(θ,φ)的2范数来完成DOA估计的。MUSIC算法的谱估计函数被定义为：

2 改进算法流程

从MUSIC算法可知，其主要运算是阵列流型矢量的计算以及最后对谱值极大值的搜索上，若进行全向搜索由图1可知搜索范围θ∈[0,360]，φ∈[0,90]，假设搜索步长为1°，则需要搜索90×360的二维空间的计算及搜索，需要耗费较长时间，为提高MUSIC算法的运算速度，最为有效的方位即减少角度搜索范围，因而采用相关干涉仪进行初测向，根据其结果做MUSIC算法的引导角，可有效的提高MUSIC算法的运算时间。

为保证测角结果的实时性，对算法进行了改进，运算步骤如下：

1）采用相关干涉仪算法进行初测角，测角步长为2°，建立相位差表，相关运算计算出初始方位角φ0，俯仰角θ0；

2）采用 MUSIC 算法精测角，以φ0、θ0为引导角，对方位角[φ0-5,φ0+5]，俯仰角[θ0-5,θ0+5]内，以步长1°进行角度搜索，得方位角Δφ，俯仰角Δθ。

验证运算速度及测角精度，设置MATLAB仿真条件：均匀圆阵，阵元数为5，信噪比为10 d Bm时仿真结果如表1所示。

表1 不同算法的测向时间及精度

可知相同条件下，本文改进算法运算速度小于相关关干涉仪，MUSIC算法，且测角精度也高于两种算法。既保留了MUSIC算法的高精度测向，在运算时间上也能满足工程应用。在不同信噪比下测试上述各算法，所得结果如图2所示。

从仿真结果来看，采用改进的基于相关干涉仪的空间谱估计算法，在实时性以及测角精度都有较大的提高，既保留了MUSIC算法的高精度测角，也能满足工程应用要求的实时性。

图2 不同信噪比下测角误差分析

3 结束语

本文提出了一种相关干涉仪与MUSIC算法相结合的改进测向算法，该算法首先采用相关干涉仪算法进行初测角，通过初测角结果减小MUSIC算法的搜索范围，进而采用MUSIC测向算法进行高精度测角。该方法效减少了MUSIC算法的运算量，既满足了实时性要求又提高了测向精度。