基于改进粒子群优化算法的无人机路径规划研究

胡丁丁 梁翀

摘要：粒子群优化（PSO）算法是一种具有过早收敛和易于停滞的简单方法。在使用PSO解决路径规划问题时， 效率损失和次优解决方案经常发生。因此，本文提出了一种通过使用Rauch–Tung–Striebel（RTS）滤波器来优化影响PSO算法性能参数的方法。此外，使用RTS滤波器消除PSO更新位置的不规则误差，并平滑生成的路径。实验结果表明，该方法基 于PSO并结合RTS算法，在无人机路径规划问题的解决方案质量和鲁棒性方面均优于现有方法。

关键词：路径规划;无人机;蜂群算法;复合形法;寻优耗时

中图分类号：V249.1    文献标识码：A       文章编号：1007-9416（2020）04-0000-00

0引言

為了满足无人机航路规划问题的多重需求，避免锯齿形航迹，本文提出一种基于粒子群优化算法（PSO）的新方法，该算法具有粒子群搜索算法优良的搜索和更新能力，以及粒子群算法的适用性，实时动态规划。由于PSO算法的最优解始终是离散的，因此易导致出现次优解。PSO离散解决方案的额外随机性会导致计划的路径曲折，这些曲折的飞行速度很高，无法被遵循[1]。

为了提高PSO算法的性能，采用了Rauch-Tung-Striebel（RTS）滤波器与粒子群算法相结合的算法，相比于传统算法和粒子群优化算法，本文提出的算法具有更好的准确性和鲁棒性，并且在离散结果平滑中具有很大的实用性。此外，RTS可以消除PSO算法计划的路径的额外随机性。这样，通过RTS滤波器改进的PSO算法具有比PSO算法更好的性能， 并且可以为固定翼无人机提供平滑合理的飞行路径。基于以上所述，基于改进粒子群优化算法，与其他现有算法相比，该方法获得了更好的解决方案。

本文的其余部分安排如下：第1节介绍了该方法的详细说明，第2节给出了实验结果，以及和其他算法的比较，最后，通过对结果的总结说明了结论。

1方法介绍

本节介绍了本文中使用的算法。我们首先介绍了PSO算法，然后基于此，提出了一种改进的PSO算法。

1.1粒子群优化算法（PSO）

粒子群优化算法是人们通过鸟群捕食行为的研究演化而来。其基本思想是通过群体中个体之间的协作和信息共享来寻找最优解[2]。？

PSO算法假设鸟群中的鸟是一种无质量的粒子，该粒子具有位置和速度两个属性，其中位置代表移动的方向，速度代表移动的快慢。单个粒子在自身的搜索空间中寻找最优解，并将其记为当前个体最优值。将个体最优值与整个粒子群里的所有粒子共享，找到最优的那个个体最优值作为整个粒子群的当前全局最优解，所有粒子均根据当前自身最优值和其他粒子共享的当前全局最优值来调整自己的位置和速度。

1.2改进粒子群优化算法

与TSP问题的离散性不同，路径规划问题是在2维或3维空间中搜索最优连续路径。因此，为解决连续路径规划问题（或类似问题），本文提出了一种学习因子自适应的基于PSO优化的方法。学习率自适应可避免粒子不规则运动带来的随机误差。换句话说，计划的之字形路径将更加平滑，以适应固定翼无人机。

下面给出所提出算法的实现细节，具体步骤如下：

步骤1：随机初始化速度v_（i，k） （i=1，k=1，2，…，n）和位置x_（i，k） （i=1，k=1，2，…，n），n表示粒子数;

步骤2：寻找当前个体最优值pbest_i和群体最优值下的当前个体数值gbest_i

步骤3：根据以下公式更新当前速度和位置：

v_（i+1，k）=〖ω_i？v〗_（i，k）+c_（1，i）？rand（）？（pbest_i-x_i ）+c_（2，i）？rand（）？（gbest_i-x_i）

x_（i+1，k）=x_（i，k）+v_（i+1，k）

其中ω是惯性因子，其值非负，默认初始值为0.5，c_1和c_2是学习因子，默认初始值取2，rand（）表示介于0，1之间的随机数，v_（i+1，k）的最大值为V_max（大于0），若v_（i+1，k）>V_max，则v_（i+1，k）=V_max。

步骤4：更新粒子当前个体最优位置和群体的最优位置。

步骤5：更新学习因子和惯性因子，如下所示

ω_（i+1）=ω_i？（1-γ）

c_（1，i+1）=c_（1，i）？（1-γ）

c_（2，i+1）=c_（2，i）？（1-γ）

其中γ表示学习因子更新速率，本文中取0.99。

步骤6：判断当前位置和速度是否满足条件，若满足，不再更新，否则回到步骤3继续迭代。

2仿真实验

改进的PSO可以应用于2维或3维连续问题。为了保持精度，实验过程保留了一般性，并且在路径规划中改进了PSO。针对无人机在三维空间中的路径规划问题进行了分析。

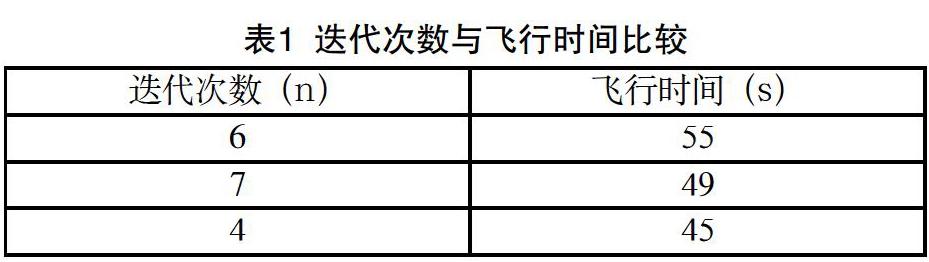
提出的改进的PSO算法是一种学习因子自适应的复杂方法。为了更好地说明算法性能，我们分别对传统PSO算法、人工蜂群算法以及改进PSO算法进行了仿真，仿真结果表明改进PSO算法可以获得更好的结果并显示出更强的稳定性，如表1所示。

3结语

為了解决路径规划问题，提出了一种基于PSO学习因子自适应的方法。该方法可以通过平滑计划并消除结果的额外随机性来提高PSO算法的性能。通过与第3部分中的其他路径规划方法进行比较，对提议的方法的有效性进行了实验检验，并通过设计的适合度函数（包括路径的长度和高度）考虑平均值，从而验证了性能。从实验结果来看，可以得出结论：本文提出的算法性能要比其他算法更好。

参考文献

[1] 赵启兵，刘勇.多旋翼飞行器的可控度分析[J].航空学报，2017，38（S1）：163-170.

[2] 庞庆霈，李家文，黄文浩.四旋翼飞行器设计与平稳控制仿真研究[J].电光与控制，2012，19（3）：51-55.

收稿日期：2020-03-02

基金项目：国网信息通信产业集团安徽继远软件有限公司综合计划项目（基于蜂群算法的无人机群协同作业关键技术研究与应用）。

作者简介：胡丁丁（1989—），男，安徽安庆人，硕士，工程师，研究方向：电力人工智能技术研究。

Research on UAV Path Planning Based on Improved Particle Swarm Optimization Algorithm

HU Ding-ding， LIANG Chong

（Anhui Jiyuan Software Co.， Ltd.， Hefei Anhui  230088）

Abstract： Particle Swarm Optimization （PSO） algorithm is a simple method with premature convergence and easy stagnation. When using PSO to solve path planning problems， efficiency losses and suboptimal solutions often occur. Therefore， this paper proposes a method to optimize the performance parameters of the PSO algorithm by using a Rauch–Tung–Striebel （RTS） smoother. In addition， an RTS smoother is used to eliminate irregular errors in the PSO update position and smooth the generated path. Experimental results show that this method is based on PSO and RTS algorithm， and it is superior to existing methods in terms of solution quality and robustness of UAV path planning problems.

Key words： path planning; UAV; bee Colony Algorithm; complex Method; optimization Time