考虑降雨影响的路堑高边坡变形监测点优化布置研究

何乃福，张 飞1,*，潘 童1,，吴为东

(1.河海大学 岩土力学与堤坝工程教育部重点实验室，江苏 南京 210098；2.江苏省岩土工程研究中心，江苏 南京 210098；3.杭州都市高速公路有限公司，浙江 杭州 310024)

边坡安全一直是公路建设和交通运输中的重要问题之一，一旦发生滑坡灾害将严重影响交通安全，因而边坡安全监测至关重要。边坡安全监测主要以位移情况来判断其稳定状态，需要重点监测边坡变形[1]。目前边坡变形监测技术[2]主要分为：非接触式监测(如激光扫描、合成孔径雷达等)和接触式监测(如大地测量、GNSS变形监测等)，其中接触式监测技术应用较为广泛，但是需要预先布置多个监测点。先进的接触式监测技术能够实现实时动态监测，然而需要兼顾成本和效果，合理布置监测点。监测点位的选取既要能全面体现边坡的变形趋势，又要能准确反映边坡安全状态，因此需要优化监测点布置。

目前边坡变形监测点布置优化方法主要分为两种：经验法和优化理论分析法(如灰色理论、模糊识别等)。经验法[3]大多依据数值分析，初步判断边坡变形情况并划分变形区域，依据工程经验将监测点布置在变形较大和变形较敏感处，但这种选点方法过于依赖经验，具有较强的主观性。优化理论分析法[4-6]基于数值分析获得的边坡变形结果，运用相关优化方法分析拟监测点与边坡稳定性之间的关系，优化监测点布置。王洪德等[7]运用FLAC数值软件和模糊识别理论，考虑裂隙、软夹层等结构，提出链子崖危岩体地表位移监测点布置方法。吴浩[8]等运用ANSYS和灰色理论，综合考虑工程经验和理论分析，提出敏感度与关联度联合优化测点布置的方法。这些方法仅考虑了不降雨情况(下简称正常工况)下进行监测点布置优化，尚未考虑降雨对边坡变形监测点布置的影响。降雨作用极易引起边坡变形，甚至产生滑坡灾害，有必要考虑降雨影响对边坡变形监测点布置进行优化。本文考虑了降雨对边坡变形的影响，通过FLAC有限差分软件建立边坡模型，基于强度折减法研究正常工况和降雨工况下边坡变形特点，运用灰色理论分析拟测点变形与折减系数的关联度，提出监测点优化布置方法。

1 分析方法

本文运用FLAC中两相流模块(TP flow)，模拟非饱和土的降雨入渗，基于强度折减法计算拟监测点在不同折减系数及降雨作用下，边坡的变形情况，最后利用灰色关联度计算拟监测点位移与边坡稳定性的关联度，从而实现降雨作用下边坡监测点优化布置。

1.1 有限差分基本原理

1.1.1 强度折减法

强度折减法[9]是指在数值计算中，通过不断降低土层的抗剪强度参数直到边坡达到极限破坏状态。此时，折减系数即为该计算边坡的安全系数。对于满足MC条件的土体，抗剪强度参数折减方法如下：

τf=cf+σtanφf

(1)

cf=c/Fs

(2)

tanφf=tanφ/Fs

(3)

式中：Fs为折减系数；τf为折减后土体的抗剪强度；cf、φf为折减后土体黏聚力和摩擦角。

1.1.2 土体本构和屈服准则

本文采用MC本构模型描述土体应力应变关系，屈服准则的确定和土体所处的状态有关。当FLAC中的两相流模块打开，土体处于非饱和状态，需要考虑基质吸力的影响，按公式(4)的屈服准则[10]判断土体状态；当土体处于饱和状态时，屈服准则变成莫尔-库仑屈服判据。

τmax=(σ-Pa)tanφf+Sw(Pa-Pw)tanφf+cf

(4)

式中：τmax为土体抗剪强度，Pa为孔隙气压力、Pw孔隙水压力。

1.2 降雨入渗基本原理

1.2.1 非饱和渗透

在FLAC两相流理论[11]中，土体孔隙被水和空气两种流体完全填充，并且用流动系数来表示土体渗透性的强弱。土体流动系数k(m2/Pa-sec)和渗透系数ks(m/s)的换算公式为：k=ks×1.02×10-4。两种流体的移动方式用达西定律表示：

(5)

(6)

1.2.2 土-水特征曲线

土-水特征曲线描述的是基质吸力和含水量之间的关系。本文运用传统的Van Genuchten(VG)模型[12]来描述土层的土-水特征曲线。FLAC数值软件中，采用标准化饱和度(Ss)[13]表示VG模型，其表达式为：

(7)

(8)

(9)

式中：Ss为土体标准化饱和度，Sw为土体饱和度，Sl为土体残余饱和度，P0、b、c、d为公式拟合参数，krel为土体相对渗透系数。

1.3 灰色关联度分析

灰色关联度分析方法[14]的原理是依据参考序列及各个相关因素序列增长变化相似程度，来判断两者之间紧密度。

(10)

式中，i=0，1，2，…，m；n表示有n个相关因素；m表示每个相关因素有m个测试数据。

(11)

式中，γij是j个相关因素的第i个测试数据与相应折减系数的关联系数；k=0，1，2，…，n；m和M分别为差序列Δi(k)中的极小值和极大值；ξ∈(0,1)是相关度参数。

(12)

式中，γj表示第j个相关因素与折减系数之间的关联度。

求解灰色关联度时，依据上述公式编写灰色关联度MATLAB计算程序，将正常工况和降雨工况下的X0和Xi序列输入计算程序中，计算拟监测点的位移与边坡稳定性的关联度。

2 方法应用

2.1 工程概况

本文以杭州某高速公路路堑边坡为例，研究其变形监测点优化布置方法。该段路堑边坡长140 m，最大坡高约56 m，设计为五级坡，每级坡高10 m，第五级开挖到顶，边坡样式如图1所示。地质特征从上到下分别为，顶部表层是1～2 m含碎石粉质粘土；基岩是13～15 m强风化辉绿岩；下层为中风化辉绿岩。工程区处于亚热带季风气候区，降雨频繁，极易诱发边坡滑坡灾害。

图1 路堑边坡示意图Fig.1 Schematic diagram of cutting slope

2.2 数值模拟

FLAC两相流模板(Tp flow)可以模拟气相和液相在土体中的流动，对非饱和土边坡降雨入渗进行分析[11]。运用FLAC软件中的两相流模板，在模型上先拟布设监测点位，采用强度折减法，求取边坡的安全系数并模拟其破坏过程，利用FISH语言编写相应程序记录各个拟布点的位移变化。

由于地勘资料有限，地貌起伏不定，假定不考虑地层起伏的影响，将路堑边坡断面简化，所分析断面数值模型见图2。根据现场地质勘查以及相关室内试验，结合相关规范和文献综合分析得到岩土体物理力学参数。计算参数取值见表1，其中降雨量参考我国城市暴雨强度公式查询表，取50年一遇降雨6 h的最大降雨强度，即6.894 44e-6 m/s。

图2 边坡监测断面数值模型Fig.2 Numerical model of slope monitoring section

3 监测点优化布置方法

计算正常工况、降雨持时分别为12、24、36 h情况下，边坡的安全系数及变形情况。图3给出了相应的边坡水平位移分布情况，发生降雨时边坡破坏滑动面由底部向顶部扩展，变形最大区域由第一级边坡底部变为第四级边坡底部。降雨12 h后，边坡由原来的整体破坏过度到局部破坏，因此，需要着重关注降雨时间超过12 h之后的边坡变形情况。

表1 岩土体物理力学指标Tab.1 Physical and mechanical parameters of rock and soil

利用灰色理论计算各监测点位移与安全系数之间的关联度并排序的过程，即为监测点优化布置的过程。基于上述正常工况及降雨工况下边坡稳定性分析，获得边坡强度折减计算过程中拟布点位的位移变化，输出降雨6 h 50年一遇的降雨强度下，拟布设的监测点在不同强度折减系数下的位移值。当边坡破坏，即测点位移突变或边坡塑性区贯通时，停止计算。折减系数较小时，各监测点变形量较小，对此时的位移进行关联度分析没有意义；只有接近破坏时，监测点变形量与折减系数的关联度才能指导预警工作。表2中给出降雨36 h情况下折减系数1.05～1.11范围内的各拟布点位移值，并以此来构建灰色关联分析的关系序列。然后利用上述灰色理论计算降雨工况下拟监测点水平位移与强度折减系数之间的关联度值，计算结果如表3所示。以同样方式计算正常工况和降雨12、24 h情况下水平位移与强度折减系数关联度，结果如图4所示。

表3 降雨36 h监测点水平位移与折减系数关联度Tab.3 Correlation between horizontal displacement and reduction coefficient at rainfall for 36 h

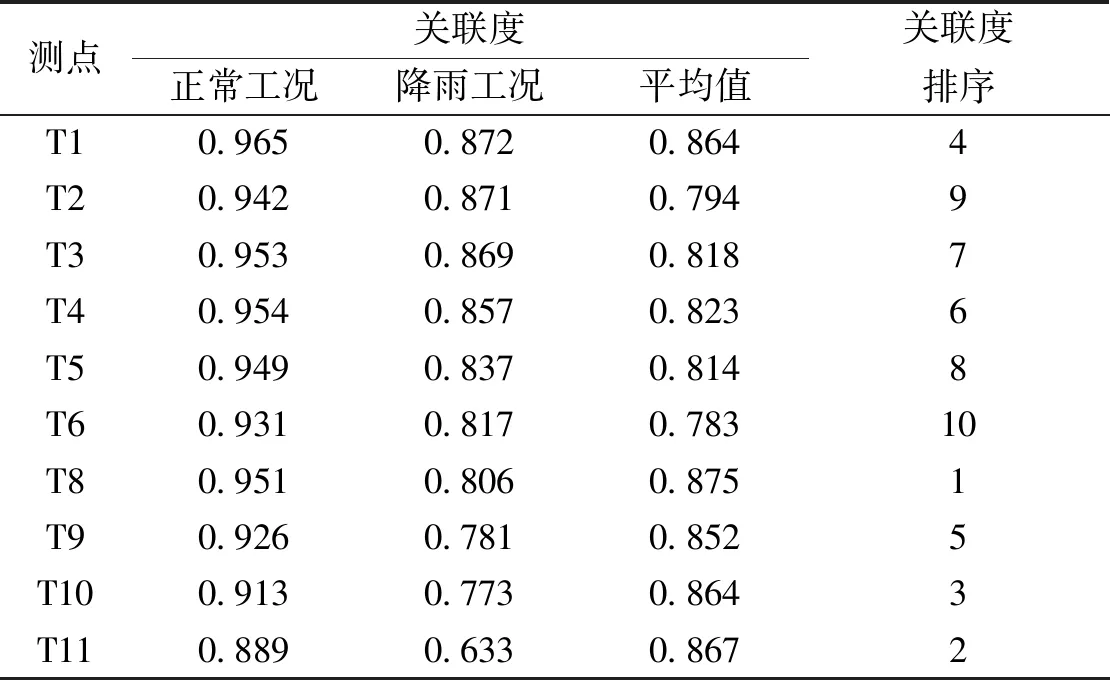
表4 正常工况和降雨工况下的关联度Tab.4 Correlation under normal and rainfall conditions

图4 各种工况下各监测点相应的关联度Fig.4 Correlation of monitoring points under various conditions

图4给出了各种工况下拟监测点的关联度计算结果，可以发现：无论是正常工况还是降雨工况下，监测点T7对应的关联度都很小，说明该类点的水平位移变化规律与边坡稳定性相似度不高，因而该类点位不适宜作为边坡变形监测点。按土层分类，分别分析各测点在正常工况下相应的关联度，发现接近各土层底部的测点对应的关联度比较高，并且由土层底部向土层顶部逐渐减小，这与现有的监测点布设研究结论基本一致。随着降雨的持续，测点T9—T11的关联度逐渐与T8的结果相接近，说明上部土层测点位移与折减系数的关联度受降雨影响显著。由于降雨24 h后，边坡安全系数为1.19，更接近规范规定的预警值1.15。因此，取剩余10个监测点正常工况和降雨24 h下的关联度，取平均值并排序，结果如表4所示。综合考虑两种工况与折减系数的关联度，监测点应优先布置在T8、T11、T10、T1、T9、T4、T3处；考虑施工和安装的便宜程度，建议将监测点布置在平台上，因此选取T1、T3、T9和T11为监测点。

4 结论

1)正常工况下，边坡破坏形式为整体破坏，降雨工况下破坏形式为局部破坏。正常工况下边坡坡脚处变形与边坡稳定的关联度较大，降雨工况下边坡坡顶处关联度较大，需要重点对坡脚及坡顶两处的变形进行监测。

2)本文提出的监测点优化布置方法，避开了不必要的监测点，使得监测数据更有利于指导预警工作，对经济合理地布置监测点具有一定的指导意义。该方法综合考虑正常工况和降雨工况，更接近于工程实际，为监测点布置提供决策依据。

本文提出的监测点优化布置方法，具有较强的实用性。但本文在关联度分析过程中，取两种工况的平均值，具有一定的局限性。在以后的研究中，可以考虑两种工况的权重或多种触发因素，对监测点优化布设展开研究。