去3 度点的Pósa- 条件的性质研究*

张岳

（海南广播电视大学，海南 海口570208）

1 概述

本文中所涉及的图均为有限图，未明确给出的定义和概念均以[1]中为准。令D是一个定向图，A是一个阿贝尔群（“0”为单位元的加法群），φ：E（D）→A 是一个函数，如果0∉φ（E（D）），则称φ 是处处不为零的。对每个顶点ν∈V（D），设函数∂φ：V（D）→A 为∂φ（ν）=∑e∈E+（ν）φ（e）-∑e∈E-（ν）φ（e）且有∑v∈V（D）∂φ（ν）=0。如果∂φ 的值恒等于零，则称φ 为流或A- 流。之后Jaeger 等人[2]在研究和推广流的问题过程中又引入了群连通的概念。如果对于每个满足∑ν∈V（D）P（ν）=0 的函数p：V（D）→A，总能找到处处不为零的函数φ：E（D）→A使得∂φ=p，则称D是A- 连通的。

在[3]中，给出了一个处处不为零的流的存在性并不依赖于边的定向，接下来我们只讨论无向图的群连通性。

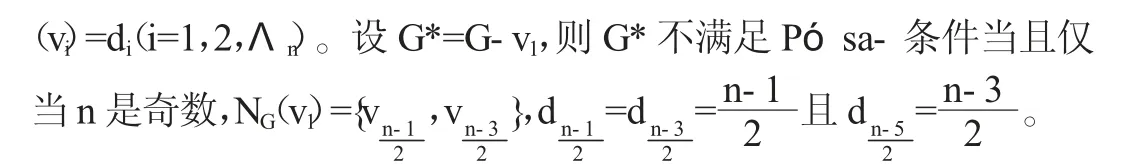
在[6] 中，Zhang和Yin 给出了满足Pósa- 条件的图是否Z3-连通的一个充分条件，但是d1=d2=3 的情况并没有解决。在本文中，将讨论满足Pósa- 条件的图去掉3 度点后是否还满足Pósa- 条件，这将对今后讨论d1=d2=3 时满足Pósa- 条件的图是否Z3- 连通奠定基础。

2 主要结论

定理2 设G是n 阶简单图（n≥9），G满足Pósa- 条件，π（G）=（d1，d2，Λdn），其中3=d1≤d2≤Λ≤dn，V（G）={v1，v2，Λ，vn}且dG（vi）=di（i=1，2，Λ，n）。设G*=G-v1，NG（v1）={vp，vq，vs}（p＜q＜s），则G*不满足Pósa- 条件当且仅当G属于以下四种情况。

证明：设π（G*）=（d1*，d2*，Λdn-1*），其中d1*≤d2*≤Λ≤dn-1*。设lG*（v）表示dG*（v）在π（G*）中的位置序号，其中v≠v1。我们考虑以下两种情况。

情形1 n 是偶数